Euler-Mascheroni-Konstante

$\gamma$

Die Euler-Mascheroni-Konstante (nach den Mathematikern Leonhard Euler und Lorenzo Mascheroni), auch Eulersche Konstante, ist eine wichtige mathematische Konstante, die besonders in den Bereichen Zahlentheorie und Analysis auftritt. Sie wird mit dem griechischen Buchstaben $\gamma$ (Gamma) bezeichnet.

Die blaue Fläche stellt die Eulersche Konstante dar.

Ihre Definition lautet:

$\gamma =\lim _{n\to \infty }\left(H_{n}-\ln n\right)=\lim _{n\rightarrow \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln n\right)=\int _{1}^{\infty }\left({1 \over \lfloor x\rfloor }-{1 \over x}\right)\,\mathrm {d} x,$

wobei $H_{n}$ die n-te harmonische Zahl, $\ln$ den natürlichen Logarithmus und $\lfloor x\rfloor$ die Abrundungsfunktion bezeichnet.

Ihr numerischer Wert ist auf 100 dezimale Nachkommastellen genau (Folge A001620 in OEIS):

γ = 0,57721 56649 01532 86060 65120 90082 40243 10421 59335 93992 35988 05767 23488 48677 26777 66467 09369 47063 29174 67495 …

Mit Stand vom November 2009, Berechnung abgeschlossen am 13. März 2009, sind 29.844.489.545 dezimale Nachkommastellen bekannt.

Allgemeines

Trotz großer Anstrengungen ist bis heute unbekannt, ob diese Zahl rational oder irrational, ob sie algebraisch oder transzendent ist. Es wird aber stark vermutet, dass sie zumindest eine irrationale Zahl ist. Den ersten konkreten Beweisversuch hierzu unternahm 1926 Paul Émile Appell mit Hilfe der unten genannten Entwicklung von Joseph Ser. Durch Berechnung der Kettenbruchentwicklung von γ (Folge A002852 in OEIS)

γ = [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, 11, 3, 7, 1, 7, 1, 1, 5, 1, 49, 4, 1, 65, 1, 4, 7, 11, 1, 399, 2, 1, 3, 2, 1, 2, 1, 5, 3, 2, 1, …]

erhält man untere Schranken für positive ganze Zahlen p und q mit γ = p/q (zum Beispiel ergeben 475.006 Teilnenner q > 10^244.663).

Im Gegensatz zu Quadratwurzeln aus rationalen Zahlen beim Satz des Pythagoras und zur Kreiszahl $\pi$ bei Umfang und Fläche eines Kreises mit rationalem Radius tritt die Eulersche Konstante bei endlichen Elementargeometrischen Problemen nicht auf. Es gibt jedoch viele technische Probleme, die auf die Summierung der endlichen harmonischen Reihe $H_{n}$ führen, wie etwa das Schwerpunktproblem des freitragenden Auslegers, das Problem der optimalen Sitzreihen-Erhöhung in Theatern und Kinos. Die Eulersche Konstante tritt bei vielen Problemen der Analysis, Zahlentheorie und Funktionentheorie und insbesondere bei speziellen Funktionen auf.

Konvergenz

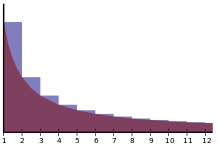
Die Existenz der Eulerschen Konstanten ergibt sich aus der Teleskopsumme

$\gamma =\lim _{n\rightarrow \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n+1)\right)=\sum _{k=1}^{\infty }\left({\frac {1}{k}}-\ln {\frac {k+1}{k}}\right)$

die wegen $0<{\tfrac {1}{k}}-\ln {\tfrac {k+1}{k}}<{\tfrac {1}{k^{2}}}$ nach dem Majorantenkriterium konvergiert.

Die Euler-Mascheroni-Konstante in mathematischen Problemen

Die Eulersche Konstante tritt in der Mathematik sehr häufig und manchmal auch ganz unerwartet in unterschiedlichen Teilgebieten auf. Hauptsächlich tritt sie bei Grenzwertprozessen von Zahlenfolgen und Funktionen, sowie bei Grenzwerten der Differential- und Integralrechnung auf. Das Auftreten lässt sich (wie auch bei anderen mathematischen Konstanten) je nach Art des Grenzwertes so unterteilen:

1. Als Funktionswert oder Grenzwert von Speziellen Funktionen.

Der Wert $\gamma$ ist das Negative der Ableitung der Gammafunktion an der Stelle 1, also

$\Gamma ^{\prime }(1)=\psi (1)=-\gamma$ .

Hieraus ergeben sich die folgenden Grenzwertdarstellungen, wobei $\zeta (s)$ die Riemannsche Zeta-Funktion und $\psi (z)$ die Digamma-Funktion bezeichnet:

$\lim _{s\to 1}\left(\zeta (s)-{\frac {1}{s-1}}\right)=\gamma$

$\lim _{z\to 0}\left\{\Gamma (z)-{\frac {1}{z}}\right\}=\lim _{z\to 0}\left\{\psi (z)+{\frac {1}{z}}\right\}=-\gamma$

$\lim _{z\to 0}{\frac {1}{z}}\left\{{\frac {1}{\Gamma (1+z)}}-{\frac {1}{\Gamma (1-z)}}\right\}=2\gamma$

$\lim _{z\to 0}{\frac {1}{z}}\left\{{\frac {1}{\psi (1-z)}}-{\frac {1}{\psi (1+z)}}\right\}={\frac {\pi ^{2}}{3\gamma ^{2}}}$

2. In Entwicklungen spezieller Funktionen, z. B. bei der Reihenentwicklung des Integrallogarithmus von Leopold Schendel, der Besselfunktionen oder der Weierstraß'schen Darstellung der Gammafunktion.

3. Bei der Auswertung bestimmter Integrale.

Hier gibt es eine reichhaltige Fülle, zum Beispiel:

${\begin{aligned}\gamma &=-\int _{0}^{1}\ln(-\ln x)\,\mathrm {d} x\\\gamma &=-\int _{0}^{\infty }e^{-x}\ln x\,\mathrm {d} x\\\gamma &=\int _{0}^{\infty }\left({\frac {1}{e^{x}-1}}-{\frac {1}{xe^{x}}}\right)\mathrm {d} x\\\gamma &=\int _{0}^{1}\left({\frac {1}{\ln x}}+{\frac {1}{1-x}}\right)\mathrm {d} x\\\gamma &={\frac {1}{2}}+2\int _{0}^{\infty }{\frac {\sin(\arctan x)}{(e^{2\pi x}-1){\sqrt {1+x^{2}}}}}\mathrm {d} x\end{aligned}}$

oder auch

${\begin{aligned}\int _{0}^{\infty }e^{-x}\ln ^{2}x\,\mathrm {d} x&\;=\;{\frac {\pi ^{2}}{6}}+\gamma ^{2}\\\int _{0}^{\infty }e^{-x^{2}}\ln x\,\mathrm {d} x&\;=\;-{\frac {\sqrt {\pi }}{4}}(\gamma +2\ln 2)\end{aligned}}$

Es gibt auch sehr viele invariante Parameterintegrale, z. B.:

${\begin{aligned}\gamma &=\int _{0}^{\infty }\left({\frac {1}{x^{k}+1}}-e^{-x}\right){\frac {\mathrm {d} x}{x}},\quad k>0\\\gamma &=\int _{0}^{\infty }\left({\frac {1}{kx+1}}-e^{-kx}\right){\frac {\mathrm {d} x}{x}},\quad k>0\end{aligned}}$

Man kann $\gamma$ auch als ein Doppelintegral mit der äquivalenten Reihe ausdrücken:

$\gamma =\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1-x\,y)\ln(x\,y)}}\,\mathrm {d} x\,\mathrm {d} y=\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

Es gibt einen interessanten Vergleich (J. Sondow 2005) des Doppelintegrals und der alternierenden Reihe:

$\ln \left({\frac {4}{\pi }}\right)=\int _{0}^{1}\int _{0}^{1}{\frac {x-1}{(1+x\,y)\ln(x\,y)}}\,\mathrm {d} x\,\mathrm {d} y=\sum _{n=1}^{\infty }(-1)^{n-1}\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

In diesem Sinne kann man sagen, dass $\ln \left({\frac {4}{\pi }}\right)$ die „alternierende Eulersche Konstante“ ist.

Außerdem sind diese zwei Konstanten mit dem Paar

$\sum _{n=1}^{\infty }{\frac {N_{1}(n)+N_{0}(n)}{2n(2n+1)}}=\gamma ,$

$\sum _{n=1}^{\infty }{\frac {N_{1}(n)-N_{0}(n)}{2n(2n+1)}}=\ln \left({\frac {4}{\pi }}\right)$

von Reihen verknüpft, wobei $N_{1}(n)$ und $N_{0}(n)$ die Anzahl der Einsen bzw. der Nullen in der Binärentwicklung von sind.

Ferner gibt es eine ebenso reichhaltige Fülle an unendlichen Summen und Produkten, etwa

${\begin{aligned}e^{\gamma }&=\lim _{n\to \infty }{\frac {1}{\ln n}}\prod _{p\leq n,p{\text{ prim}}}\left(1-{\frac {1}{p}}\right)^{-1}\\{\frac {6}{\pi ^{2}}}e^{\gamma }&=\lim _{n\to \infty }{\frac {1}{\ln n}}\prod _{p\leq n,p{\text{ prim}}}\left(1+{\frac {1}{p}}\right)\\\gamma &=\lim _{x\to 1^{+}}\sum _{n=1}^{\infty }\left({\frac {1}{n^{x}}}-{\frac {1}{x^{n}}}\right)\end{aligned}}$

Die letzte Formel wurde 1998 von Sondow gefunden.

4. Als Grenzwert von Reihen. Reihendarstellungen sind jedoch im Gegensatz zu $\pi$ prinzipiell seltener. Als einfachstes Beispiel ergibt sich aus der Grenzwert-Definition:

$\gamma =\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\ln {\frac {n+1}{n}}\right)$ .

Als Beispiele von Reihen mit rationalen Gliedern sind nur die Reihen von Euler, Giovanni Enrico Eugenio Vacca, S. Ramanujan und Joseph Ser bekannt. An Reihen mit irrationalen Gliedern gibt es unzählige Variationen, deren Glieder aus rational gewichteten Werten der riemannschen Zeta-Funktion an den ungeraden Argumentstellen ζ(3), ζ(5), … bestehen. Ein Beispiel einer besonders schnell konvergierenden Reihe ist:

$\sum _{n=1}^{\infty }{\frac {\zeta (2n+1)-1}{(2n+1)2^{2n}}}=1+\ln 2-\ln 3-\gamma =$ 0,0173192269903…

Eine weitere Reihe ergibt sich aus der Kummerschen Reihe der Gammafunktion:

$\gamma =\ln \pi -4\ln \Gamma ({\tfrac {3}{4}})+{\frac {4}{\pi }}\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {\ln(2k+1)}{2k+1}}$

Bezeichnungen

Man kann sagen, dass die Eulersche Konstante diejenige Konstante mit den meisten Bezeichnungen ist. Euler selbst bezeichnete sie mit C und gelegentlich mit O oder n. Es ist jedoch zweifelhaft, ob er damit ein eigenständiges Symbol für seine Konstante einführen wollte. Mascheroni bezeichnete die Konstante nicht – wie oft behauptet – mit γ, sondern mit A. Das γ-Missverständnis rührt von dem häufig unüberprüft zitierten Artikel von J. W. L. Glaisher her (wobei Glaisher dort ausdrücklich anmerkt, dass er Mascheronis Buch nicht gesehen hat):

„Euler’s constant (which throughout this note will be called γ after Mascheroni, De Morgan, & c.) [...]
It is clearly convenient that the constant should generally be denoted by the same letter. Euler used C and O for it; Legendre, Lindman, & c., C; De Haan A; and Mascheroni, De Morgan, Boole, & c., have written it γ, which is clearly the most suitable, if it is to have a distinctive letter assigned to it. It has sometimes (as in Crelle, t. 57, p. 128) been quoted as Mascheroni’s constant, but it is evident that Euler’s labours have abundantly justified his claim to its being named after him.“

– Glaisher: On the history of Euler’s constant, 1872, S. 25 und 30

Andere Mathematiker verwenden die Bezeichnungen C, c, ℭ, H, γ, E, K, M, l. Der Ursprung der heute üblichen Bezeichnung γ ist nicht sicher. Carl Anton Bretschneider verwendete die Bezeichnung γ neben c in einem 1835 entstandenen und 1837 veröffentlichten Artikel, Augustus De Morgan führte die Bezeichnung γ in einem in Teilen von 1836 bis 1842 veröffentlichten Lehrbuch im Rahmen der Behandlung der Gammafunktion ein.

Verallgemeinerungen

Die Eulersche Konstante kennt mehrere Verallgemeinerungen. Die wichtigste und bekannteste ist die der Stieltjes-Konstanten:

$\gamma _{n}:=\lim _{N\to \infty }\left(\sum _{k=1}^{N}{\frac {\log ^{n}k}{k}}-{\frac {\log ^{n+1}N}{n+1}}\right),\quad n=0,1,2,\ldots$

Anzahl berechneter Dezimalstelle

1734 berechnete Leonhard Euler sechs Dezimalstellen (fünf gültige), später 16 Stellen (15 gültige). 1790 berechnete Lorenzo Mascheroni 32 Dezimalstellen (30 gültige), wovon jedoch die drei Stellen 20 bis 22 falsch sind – anscheinend aufgrund eines Schreibfehlers, sie sind allerdings mehrfach im Buch angegeben. Der Fehler war Anlass für mehrere Neuberechnungen.

**Anzahl veröffentlichter gültiger Dezimalstellen von γ**
Jahr	Stellen	Autor
1734	5	Leonhard Euler
1735	15	Leonhard Euler
1790	19	Lorenzo Mascheroni
1811	22	Carl Friedrich Gauß
1857	34	Christian Fredrik Lindman
1871	99	J. W. L. Glaisher
1952	328	John William Wrench, Jr.
1961	1.050	Helmut Fischer & Karl Zeller
1973	4.879	William A. Beyer & Michael S. Waterman
1976	20.700	Richard P. Brent
1997	1.000.000	Thomas Papanikolaou
1998	7.286.255	Xavier Gourdon
1999	108.000.000	Xavier Gourdon & Patrick Demichel
2009	29.844.489.545	Alexander J. Yee & Raymond Chan

Siehe auch

Meissel-Mertens-Konstante – Primzahl-Analogon zur Euler-Mascheroni-Konstante

Literatur

Laurentio Mascheronio: Adnotationes ad calculum integralem Euleri / In quibus nonnulla Problemata ab Eulero proposita resolvuntur. Petrus Galeatius, Ticini 1790–1792 (lateinisch; „A = 0,577215 664901 532860 618112 090082 39“ auf S. 23 und S. 45)
M. Lerch: Expressions nouvelles de la constante d’Euler (9. Juli 1897), Sitzungsberichte der königl. böhmischen Gesellschaft der Wissenschaften. Mathematisch-naturwissenschaftliche Classe, 1897, XLII S. 1–5
Julian Havil: Gamma: Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung. Springer, Berlin 2007, ISBN 978-3-540-48495-0.

Basierend auf einem Artikel in:

Wikipedia.de