
Digamma-Funktion
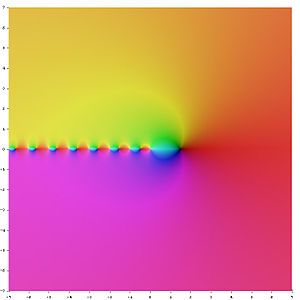
Die Digamma-Funktion oder Psi-Funktion ist in der Mathematik eine Funktion, die definiert wird als:
Sie ist also die logarithmische
Ableitung der Gammafunktion.
Die Digamma-Funktion ist die erste der Polygammafunktionen.
Bis auf ihre Pole erster Ordnung für negative ganze Argumente ist sie (genau wie
die Gammafunktion) in ganz
holomorph.
Berechnung
Die Beziehung zur harmonischen Reihe
Die Digammafunktion, welche meist als ψ0(x),
ψ0(x) oder
(nach der Form des vorklassischen griechischen Buchstaben Ϝ digamma) dargestellt wird,
steht mit der harmonischen
Reihe in folgender Beziehung:
wobei Hn das n-te Element der harmonischen Reihe und γ die Euler-Mascheroni-Konstante ist. Für halbzahlige Werte kann sie geschrieben werden als:
Integral-Darstellung
Die Digammafunktion kann wie folgt als Integral dargestellt werden:
Dies kann auch geschrieben werden als:
Dies folgt aus der Formel für das Euler-Integral für die harmonische Reihe.
Taylor-Reihe
Durch Reihenentwicklung der Taylor-Reihe um den Punkt z=1 kann die Digammafunktion wie folgt dargestellt werden:
Sie konvergiert für |z|< 1. Dabei ist
die Riemannsche
ζ-Funktion. Die Reihe kann leicht von der zugehörigen Taylor-Reihe für die
Hurwitzsche
ζ-Funktion hergeleitet werden.
Binomische Reihe
Die binomische Reihe für die Digammafunktion folgt aus dem Euler-Integral
wobei
der verallgemeinerte
Binomialkoeffizient ist.
Funktionalgleichung
Die Digammafunktion genügt folgender Funktionalgleichung, welche direkt aus der logarithmischen Ableitung der Gammafunktion hergeleitet werden kann:
Hiermit kann allerdings nicht ψ(1/2) berechnet werden; dieser Wert ist unten angegeben.
Rekursionsformel und Summenausdrücke
Die Digamma-Funktion genügt der Rekursionsformel
oder
wobei Δ der rechtsseitige Differenzoperator ist. Dies erfüllt die Rekursionsbeziehung der harmonischen Reihe. Daraus folgt
Allgemeiner gilt:
Aus der Gaußschen Produktdarstellung der Gammafunktion lässt sich äquivalent dazu
.
schlussfolgern.
Quotientenbeziehung zur Gammafunktion
Für den Quotienten aus Digammafunktion und Gammafunktion liefert die Produktdarstellung den Ausdruck
.
Bei positiven ganzen Zahlen ,
bei deren negativen Werten sowohl Digamma- als auch Gammafunktion divergieren,
folgt dann
.
Mit Hilfe der Funktionalgleichung für die Gammafunktion findet man sogar
heraus, dass der Wert des Quotienten ausschließlich vom Argument der
Gammafunktion abhängt, also gilt für ganzzahlige
schließlich
.
Gaußsche Summe
Die Digammafunktion hat eine Gaußsche Summe der Form
für natürliche Zahlen .
Dabei ist ζ(s,q) die Hurwitzsche
ζ-Funktion und
das Bernoulli-Polynom.
Ein Spezialfall des Multiplikationstheorem
ist
Gaußsches Digamma-Theorem
Für ganze Zahlen
und
(mit
)
kann die Digammafunktion mit elementaren
Funktionen ausgedrückt werden
Besondere Werte
Die Digamma-Funktion hat unter anderem folgende besondere Werte:
Ableitung
Die Ableitung der Digammafunktion ist nach deren Definition die Trigamma-Funktion
die zweite Polygammafunktion


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.12. 2021