
Harmonische Reihe
Die harmonische Reihe ist in der Mathematik
die Reihe,
die durch Summation der Glieder
der harmonischen
Folge entsteht. Ihre Partialsummen
werden auch harmonische Zahlen genannt. Diese finden beispielsweise
Anwendung in Fragestellungen der Kombinatorik
und stehen in enger Beziehung zur
Euler-Mascheroni-Konstante
.
Obwohl die harmonische Folge eine Nullfolge
ist, ist die harmonische Reihe divergent.
Definition
Die -te
Partialsumme
der harmonischen Reihe heißt die
-te
harmonische Zahl:
Die harmonische Reihe ist ein Spezialfall der allgemeinen harmonischen
Reihe mit den Summanden ,
wobei hier
,
siehe unten.
Der Name harmonische Reihe wurde gewählt, da jedes Glied
das harmonische
Mittel der beiden benachbarten Glieder ist:
Eigenschaften
Werte der ersten Partialsummen
Der Nenner von
ist durch jede Primzahlpotenz
mit
teilbar, also auch durch
mit
und für
nach dem Bertrandschen
Postulat durch mindestens eine ungerade Primzahl.
Insbesondere ist
für
keine ganze Zahl (Theisinger 1915).
Allgemeiner gilt, dass keine Differenz
für
eine ganze Zahl ist (József Kürschák
1918),
dies ist wiederum ein Spezialfall eines Satzes von Trygve Nagell 1923.
Ist
eine Primzahl, so ist der Zähler von
nach dem Satz
von Wolstenholme durch
teilbar, ist
eine Wolstenholme-Primzahl, dann sogar durch
.

Divergenz
Die harmonische Reihe divergiert gegen unendlich, wie zuerst Nikolaus von Oresme bewies. Man sieht dies durch Vergleich mit einer Reihe, die in jedem Glied kleiner oder gleich ist (Minorantenkriterium):
Die Summe der letzten Zeile übersteigt jeden Wert, wenn
genügend groß ist. Genauer erhält man die Abschätzung
für
Asymptotische Entwicklung
Es gilt die asymptotische Entwicklung:
Hierbei bezeichnet
den natürlichen Logarithmus,
und das Landau-Symbol
beschreibt das Verhalten des Restterms der Entwicklung für
.
Die mathematische
Konstante
(gamma) heißt Euler-Mascheroni-Konstante
und ihr numerischer Wert beträgt 0,5772156649…
Des Weiteren gilt ,
falls
.
-
-
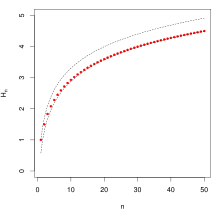
Vergleich einiger Partialsummen mit Werten der Näherungsformel Hn ≈ ln n + γ n Hn
(gerundet)Näherung
(gerundet)Genauigkeit
(gerundet)5 2,28 2,19 95,77 % 10 2,93 2,88 98,32 % 20 3,60 3,57 99,31 % 50 4,50 4,49 99,78 % 100 5,19 5,18 99,90 % 500 6,79 6,79 1 − 1·10−4 1000 7,49 7,48 1 − 7·10−5 10000 9,79 9,79 1 − 5·10−6
-
Integraldarstellung
Es gilt
.
Diese Darstellung verallgemeinert die -te
harmonische Zahl auf komplexe Werte für
mit
.
Besondere Werte der verallgemeinerten harmonischen Zahlen sind beispielsweise:
Erzeugende Funktion
Entwickelt man die Funktion
um den Entwicklungspunkt 0 in eine Taylorreihe,
so erhält man die harmonischen Zahlen als Koeffizienten:
Dies sieht man leicht ein, indem man das Cauchy-Produkt der für
absolut konvergenten Reihen von
und
bildet.
Beziehung zur Digamma-Funktion
Die -te
harmonische Zahl lässt sich durch die Digamma-Funktion
ausdrücken und auf komplexe Werte für
fortsetzen (falls
keine negative ganze Zahl ist):
.
Dabei bezeichnet
die Gammafunktion,
ihre Ableitung und
die Euler-Mascheroni-Konstante.
Reihen über harmonische Zahlen
Es gilt für die harmonischen Zahlen:
Hierbei bezeichnet
die Riemannsche
Zetafunktion.
Anwendungsbeispiel
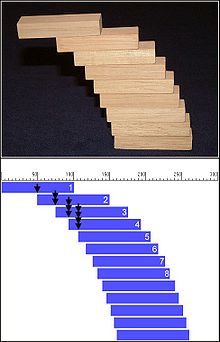
Gleichartige Klötze sollen so gestapelt werden, dass der oberste Klotz möglichst weit über den untersten ragt.
Das Bild zeigt eine Anwendung der harmonischen Reihe. Werden die horizontalen
Abstände der Klötze - von oben nach unten vorgehend - gemäß der harmonischen
Reihe gewählt, so ist der Stapel gerade noch stabil. Auf diese Weise bekommt der
Abstand zwischen dem obersten und untersten Klotz den größtmöglichen Wert. Die
Klötze haben eine Länge .
Der oberste Baustein liegt mit seinem Schwerpunkt auf dem zweiten Stein an der
Position
.
Der gemeinsame Schwerpunkt von Stein-1 und Stein-2 liegt bei
,
der von Stein-1, Stein-2 und Stein-3 bei
,
der des
-ten
Steins bei
.
Die Gesamtlänge
des Auslegers beträgt somit:
.
Jeder zusätzliche Stein entspricht einem weiteren Summanden in der harmonischen Reihe. Da die harmonische Reihe beliebig große Werte annehmen kann, wenn man sie nur weit genug fortführt, gibt es keine prinzipielle Grenze, wie weit der oberste Stein überhängen kann. Die Zahl der nötigen Steine steigt allerdings sehr rasch mit dem angestrebten Überhang. Für einen Überhang in 2,5-facher Steinlänge werden etwa 100 Steine benötigt werden. Bei einem realen Aufbau würde dies bereits hohe Anforderungen an die Maßhaltigkeit der Steine stellen.
Verwandte Reihen
Die alternierende harmonische Reihe konvergiert:
Die Konvergenz folgt aus dem Leibnizkriterium, der
Grenzwert lässt sich mit der Taylor-Entwicklung
des natürlichen Logarithmus
und dem abelschen
Grenzwertsatz berechnen. Es ist nämlich
und wenn man
setzt, erhält man in der Reihenentwicklung die alternierende harmonische
Reihe.
Als allgemeine harmonische Reihe bezeichnet man
sie divergiert für
und konvergiert für
(siehe Cauchysches
Verdichtungskriterium).
Beispiel für :
Beispiel für :
Beispiel für :
wobei
die
-te
Bernoulli-Zahl
bezeichnet.
Lässt man für
auch komplexe Zahlen zu, gelangt man zur riemannschen
Zetafunktion.
Subharmonische Reihen
Subharmonische Reihen entstehen dadurch, dass man bestimmte Summanden bei der Reihenbildung der harmonischen Reihe weglässt, etwa nur die Kehrwerte aller Primzahlen summiert:
Diese Summe divergiert ebenfalls. Eine konvergente Reihe entsteht, wenn man nur noch über die Primzahlzwillinge (oder gar Primzahldrillinge oder Primzahlvierlinge usw.) summiert; allerdings ist nicht bekannt, ob es sich dabei um unendliche Reihen handelt. Die Grenzwerte werden Brunsche Konstanten genannt.
Weitere subharmonische Reihen sind die ebenfalls konvergenten Kempner-Reihen.


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 02.10. 2022