
Polygammafunktion
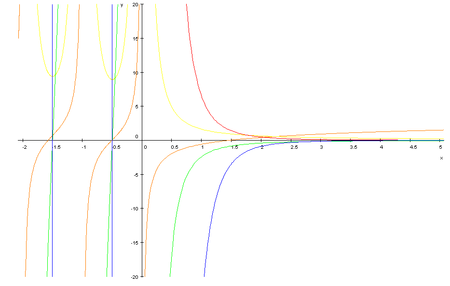
m = 0 m = 1 m = 2 m = 3 m = 4
In der Mathematik sind die Polygammafunktionen
eine Reihe spezieller
Funktionen, die als die Ableitungen
der Funktion
definiert sind. Dabei bezeichnet
die Gammafunktion und
den natürlichen Logarithmus.
Die ersten beiden Polygammafunktionen werden Digammafunktion und Trigammafunktion genannt.
 |
 |
 |
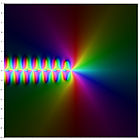 |
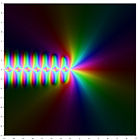 |
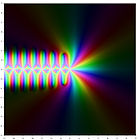 |
Notation
Die Polygammafunktionen werden mit dem kleinen griechischen Buchstaben Psi
gekennzeichnet. Bei der ersten Polygammafunktion wird der Index meist
weggelassen oder als 0 festgelegt; sie wird als Digammafunktion
bezeichnet. Die zweite Polygammafunktion, also die Trigammafunktion, hat
das Symbol
(oder seltener
)
und ist die zweite Ableitung von
.
Allgemein wird die
-te
Polygammafunktion oder Polygammafunktion der Ordnung
mit
oder
bezeichnet und als die
-te
Ableitung von
definiert.
Definition und weitere Darstellungen
Es ist
mit der Digammafunktion .
Derartige Ableitungen werden auch als logarithmische
Ableitungen von
bezeichnet.
Eine Integraldarstellung ist
für
und
Eigenschaften
Differenzengleichungen
Die Polygammafunktionen haben die Differenzengleichungen
Reflexionsformel
Eine weitere wichtige Beziehung lautet
Multiplikationsformel
Die Multiplikationsformel ist für
gegeben durch
Zum Fall
also der Digammafunktion,
siehe dort.
Reihendarstellungen
Eine Reihendarstellung der Polygammafunktion lautet
wobei
und
eine beliebige komplexe Zahl außer den negativen ganzen Zahlen ist. Die Formel
lässt sich einfacher unter Verwendung der hurwitzschen
Zetafunktion
schreiben als
Die Verallgemeinerung der Polygammafunktionen auf beliebige, nicht-ganze
Ordnungen
ist weiter
unten angegeben.
Eine weitere Reihendarstellung ist
wobei
das Kronecker-Delta
bezeichnet, die aus der Zerlegung der Gammafunktion nach dem weierstraßschen
Produktsatz folgt.
Die Taylor-Reihe
um
ist gegeben durch
die für
konvergiert.
bezeichnete dabei die riemannsche
Zetafunktion.
Spezielle Werte
Die Werte der Polygammafunktionen für rationale Argumente lassen sich meist
ausdrücken unter Verwendung von Konstanten und Funktionen wie ,
Quadratwurzel, Clausen-Funktion
,
riemannsche
ζ-Funktion, catalansche
Konstante
sowie dirichletsche
β-Funktion; z. B.
Allgemein gilt ferner:
.
Die m-te Ableitung des Tangens kann ebenfalls mit der Polygammafunktion ausgedrückt werden:
.
Darüber hinaus haben sich spezielle Werte von Polygammafunktionen als universelle Konstanten immer wieder bei einer geschlossenen Grenzwert-Beschreibung von Reihen oder auch Integralen als nützlich erwiesen, zum Beispiel gilt
Verallgemeinerte Polygammafunktion
Die verallgemeinerte Polygammafunktion erfüllt für
und
die Funktionalgleichung
wobei
die Euler-Mascheroni-Konstante
bezeichnet. Wegen
für ganzzahlige
ist die weiter oben angegebene Differenzengleichung
für natürliche
eingeschlossen.
Unter Zuhilfenahme der Hurwitzschen
-Funktion
erhält man dann die Beziehung
welche die Funktionalgleichung erfüllt.
Als Konsequenz daraus lässt sich die Verdopplungsformel
herleiten. Eine Verallgemeinerung davon lautet
die ein Äquivalent zur Gaußschen
Multiplikationsformel der Gammafunktion darstellt und die Multiplikationsformel
als Spezialfall für
enthält.
q-Polygammafunktion
Die -Polygammafunktion
ist definiert durch
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.12. 2021