
Dirichletsche Betafunktion
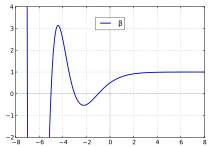
Die dirichletsche Betafunktion, geschrieben mit dem griechischen Buchstaben ,
ist eine spezielle
mathematische
Funktion, die in der analytischen
Zahlentheorie, einem Teilgebiet der Mathematik, eine Rolle spielt. Sie
bildet z.B. die Grundlage für die analytische Theorie der Verteilung der
Primzahlen in den arithmetischen Folgen
und
und ist verwandt mit der Riemannschen
Zeta-Funktion.
Benannt wurde sie nach dem deutschen Mathematiker Peter Gustav Lejeune Dirichlet (1805–1859).
Definition
Für eine komplexe
Zahl ,
deren Realteil
größer als 0 ist, ist die Beta-Funktion definiert über die Dirichletreihe:
Obwohl dieser Ausdruck nur auf der rechten Halbebene
konvergiert, stellt er die Basis für alle weiteren Darstellungen der
Beta-Funktion dar. Zur Berechnung der Beta-Funktion für alle Zahlen der
komplexen Ebene bedient man sich ihrer analytischen
Fortsetzung.
Produktdarstellung
Für die Betafunktion existiert eine Produktdarstellung, die für alle
komplexen ,
deren Realteil größer als 1 ist, konvergiert.
Hierbei impliziert ,
dass über alle Primzahlen der Form
(also
)
multipliziert wird. Analog bedeutet
,
dass über alle Primzahlen, welche die Form
besitzen (also
),
multipliziert wird.
Funktionalgleichung
Für alle
gilt die Funktionalgleichung:
Hierbei ist
die Gammafunktion.
Sie dehnt den Definitionsbereich der Beta-Funktion auf die gesamte komplexe Zahlenebene aus.
Weitere Darstellungen
Über die Mellin-Transformation
der Funktion
erhält man die Integraldarstellung:
wobei
wieder die Gammafunktion
bezeichnet.
Zusammen mit der hurwitzschen
Zetafunktion erhält man für alle komplexen
die Relation:
Eine andere gleichwertige Darstellung für alle komplexen
schließt die transzendente lerchsche
Zeta-Funktion
ein und lautet:
Spezielle Werte
Einige spezielle Werte der -Funktion
sind
Hierbei bezeichnet
die catalansche
Konstante und
ist die dritte Polygammafunktion.
Allgemein gilt für positive ganze Zahlen
die Darstellung:
wobei
die
-te
Euler-Zahl
ist. Im Fall
gilt
Insbesondere gilt für natürliche
:
Ableitung
Ein Ableitungsausdruck für alle
ist gegeben durch:
Spezielle Werte der Ableitungsfunktion sind:
(vgl. Folge ![]() A113847
in OEIS
und Folge
A113847
in OEIS
und Folge ![]() A078127 in OEIS
mit der Euler-Mascheroni-Konstante
A078127 in OEIS
mit der Euler-Mascheroni-Konstante
).
Außerdem gilt für positive ganze Zahlen :
Weiteres
Rivoal and Zudilin bewiesen 2003,
dass mindestens einer der Werte ,
,
,
,
und
irrational
ist.
Außerdem bewiesen Guillera und Sondow 2005 folgende Formel:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.11. 2024