
Tangens und Kotangens
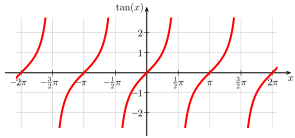
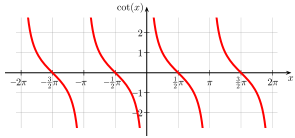
Tangens und Kotangens sind trigonometrische
Funktionen und spielen in der Mathematik
und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels
wird mit
bezeichnet, der Kotangens des Winkels
mit
.
In älterer Literatur findet man auch die Schreibweisen
für den Tangens und
für den Kotangens.
Definition
Historisch/geometrisch
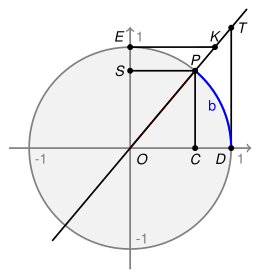
Die Bezeichnung „Tangens“ stammt von dem Mathematiker Thomas Finck (1561–1656), der sie 1583 einführte. Die Bezeichnung „Kotangens“ entwickelte sich aus complementi tangens, also Tangens des Komplementärwinkels.
Die Wahl des Namens Tangens erklärt sich unmittelbar durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge eines Tangentenabschnitts:
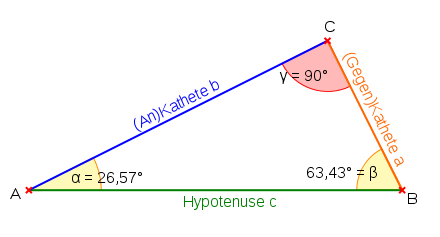
In einem rechtwinkligen Dreieck
ist der Tangens eines Winkels
das Längenverhältnis von Gegenkathete
zu Ankathete und der Kotangens das Längenverhältnis von Ankathete zu
Gegenkathete:
Daraus folgt unmittelbar:
sowie
Formal – mit Definitions- und Wertebereich
Formal kann die Tangensfunktion mittels der Sinus- und Kosinusfunktionen durch
mit
definiert werden,[1]
wobei der Wertebereich
je nach Anwendung die reellen
oder die komplexen
Zahlen
sind. Um zu verhindern, dass der Nenner
Null wird, werden beim Definitionsbereich
die Nullstellen der
Cosinus-Funktion weggelassen:
im Reellen bzw.
im Komplexen.
Der Kotangens kann analog dazu durch
mit
definiert werden, wobei sich für dessen Definitionsbereich
im Reellen bzw.
im Komplexen ergibt, wenn gewährleistet werden soll, dass der Nenner
ungleich Null ist.
Für den gemeinsamen Definitionsbereich von
und
gilt
Eigenschaften
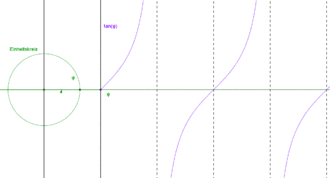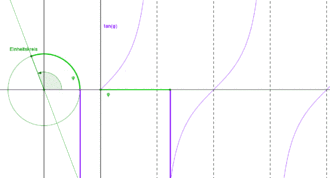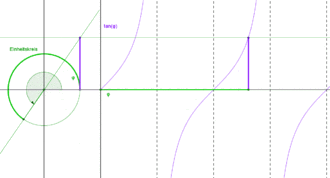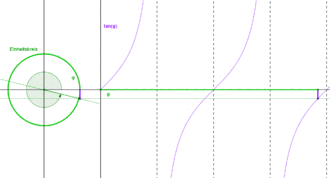
Periodizität
- Periodenlänge
(halbe Drehung):
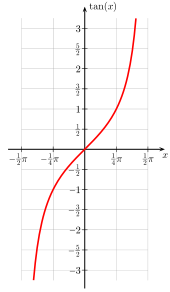
Monotonie
Tangens: Im jeweiligen Intervall streng monoton steigend.
Kotangens: Im jeweiligen Intervall streng monoton fallend.
Symmetrien
Punktsymmetrisch zum Koordinatenursprung:
Nullstellen
| Tangens: | |
| Kotangens: |
Polstellen
| Tangens: | |
| Kotangens: |
Wendestellen
| Tangens: | |
| Kotangens: |
Sowohl die Tangensfunktion als auch die Kotangensfunktion haben Asymptoten, aber keine Sprungstellen oder Extrema.
Wichtige Funktionswerte
| Tangens | Kotangens | Ausdruck | num. Wert |
|---|---|---|---|
| 0 | |||
| 0,2679491… | |||
| 0,3249196… | |||
| 0,4142135… | |||
| 0,5773502… | |||
| 0,7265425… | |||
| 1 | |||
| 1,7320508… | |||
| 2,4142135… | |||
| 3,7320508… | |||
| Polstelle |
Umkehrfunktion
Durch passende Einschränkung der Definitionsbereiche erhält man eine Bijektion
- Tangens
.
Ihre Umkehrfunktion
heißt Arkustangens und ist folglich ebenfalls bijektiv.
- Kotangens
.
Ihre Umkehrfunktion
heißt Arkuskotangens und ist folglich ebenfalls bijektiv.
Reihenentwicklung
- Tangens
- Die Taylorreihe
mit dem Entwicklungspunkt
(Maclaurinsche Reihe) lautet für
Dabei sind mit
die Bernoulli-Zahlen
bezeichnet.
- Kotangens
- Die Laurent-Reihe
lautet für
Die Partialbruchzerlegung
des Kotangens lautet für
Ableitung
Bei der Ableitung von Tangens und Kotangens tauchen die ansonsten eher wenig gebräuchlichen trigonometrischen Funktionen Sekans und Kosekans auf:
Die -ten
Ableitungen lassen sich mit der Polygammafunktion
ausdrücken:
Stammfunktionen
- Tangens
mit
.
- Kotangens
mit
.
Komplexes Argument
mit
mit
Additionstheoreme
Die Additionstheoreme für Tangens und Kotangens lauten
Aus den Additionstheoremen folgt insbesondere für doppelte Winkel
Darstellung des Sinus und Kosinus mithilfe des (Ko-)Tangens
Die Auflösung der bereits aus dem obigen Abschnitt Ableitung bekannten Identitäten
nach
bzw.
ergibt bei Beschränkung auf den ersten Quadranten zunächst einmal
Einfaches:
für
für
Die etwas komplizierteren Erweiterungen auf ganz
lassen sich entweder kompakt als Grenzwert
mit Hilfe der Floor-Funktion
oder elementarer mittels abschnittsweise definierter Funktionen
darstellen:
Rationale Parametrisierung
Der Tangens des halben Winkels kann dazu verwendet werden, verschiedene
trigonometrische Funktionen durch rationale Ausdrücke zu beschreiben: Ist ,
so ist
Insbesondere ist
eine Parametrisierung des Einheitskreises mit Ausnahme des Punktes
(der dem Parameter
entspricht). Einem Parameterwert
entspricht dabei der zweite Schnittpunkt der Verbindungsgeraden
von
und
mit dem Einheitskreis (s.a. Einheitskreis#Rationale
Parametrisierung).
Anwendung: Tangens und Steigungswinkel
Der Tangens liefert eine wichtige Kennzahl für lineare Funktionen: Jede lineare Funktion
besitzt als Graphen
eine Gerade. Der Tangens des (orientierten) Winkels
zwischen der positiven x-Richtung
und der Geraden ist die Steigung
der Geraden, d.h.
.
Dabei ist es egal, welche der beiden Halbgeraden man als zweiten Schenkel wählt.
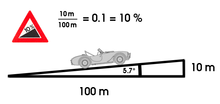
Auch unter der Steigung einer Straße versteht man den Tangens des Steigungswinkels. Das Beispiel im Bild rechts zeigt eine Steigung von 10 % entsprechend einem Steigungswinkel von etwa 5,7° mit dem Tangens von 0,1.
Anwendung in der Physik
Tangens und Kotangens können benutzt werden, um die zeitliche Abhängigkeit
der Geschwindigkeit
beim Wurf eines Körpers nach oben zu beschreiben, wenn für den Strömungswiderstand
der Luft eine turbulente
Strömung angesetzt wird (Newton-Reibung).
Das Koordinatensystem werde so gelegt, dass die Ortsachse nach oben zeigt. Für
die Geschwindigkeit gilt dann eine Differenzialgleichung der Form
mit der Schwerebeschleunigung
g und einer Konstanten k > 0. Dann ergibt sich:
,
wobei
die Grenzgeschwindigkeit ist, die beim Fall
mit Luftwiderstand erreicht wird. Wegen der oben angegebenen engen
Zusammenhänge zwischen Kotangens und Tangens kann man diese zeitliche
Abhängigkeit auch genauso gut mit Hilfe des Tangens ausdrücken:
.
Diese Lösung gilt, bis der Körper den höchsten Punkt seiner Bahn erreicht hat
(also wenn v = 0 ist, das heißt für ),
daran anschließend muss man den Tangens
hyperbolicus verwenden, um den folgenden Fall mit Luftwiderstand zu beschreiben.
Differentialgleichung
Der Tangens ist eine Lösung der Riccati-Gleichung
.
Faktorisiert man die rechte Seite, so erhält man
mit der imaginären
Einheit .
Der Tangens (als komplexe Funktion) hat die Ausnahmewerte
,
:
Diese Werte werden niemals angenommen, da die konstanten Funktionen
und
Lösungen der Differentialgleichung sind und der Existenz- und Eindeutigkeitssatz
ausschließt, dass zwei verschiedene Lösungen an derselben Stelle denselben Wert
besitzen.
Siehe auch
Anmerkungen


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.12. 2021