Rechtwinkliges Dreieck
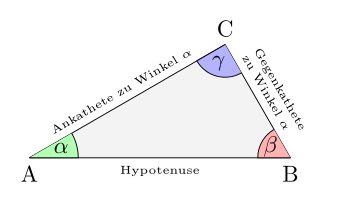
Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel.
Bezeichnungen
Als Hypotenuse[1] bezeichnet man die längste Seite eines rechtwinkligen Dreiecks. Sie liegt dem rechten Winkel gegenüber.
Als Kathete (aus dem griechischen
káthetos, das Herabgelassene, Senkblei) wird jede der beiden kürzeren
Seiten in einem rechtwinkligen Dreieck bezeichnet. Die Katheten sind also die
beiden Seiten des rechtwinkligen Dreiecks, die den rechten
Winkel bilden. In Bezug auf einen der beiden spitzen Winkel (in der Skizze
)
des Dreiecks unterscheidet man die Ankathete dieses Winkels (die dem Winkel
anliegende Kathete) und die Gegenkathete (die dem Winkel
gegenüberliegende Kathete).
Sätze
- Die Beziehung zwischen den Längen der Katheten und der Hypotenuse
beschreibt der Satz
des Pythagoras, der auch als Hypotenusensatz bezeichnet wird. (Der Satz
lautet: Sind
und
die Seitenlängen der Katheten eines rechtwinkligen Dreiecks und ist
die Seitenlänge der Hypotenuse, so gilt die Gleichung
). Der Satz des Pythagoras ist ein Spezialfall des Kosinussatzes. Der Kosinus von
ist 0, wodurch sich die Formel deutlich vereinfacht.
- Anders formuliert besagt der Satz
des Pythagoras, dass die Summe der Flächeninhalte
der beiden Quadrate über den Katheten
gleich dem Flächeninhalt des Quadrats über der Hypotenuse
ist. Aus dieser Tatsache folgen der Kathetensatz und der Höhensatz (siehe auch
Satzgruppe
des Pythagoras). Die Höhe
eines rechtwinkligen Dreiecks teilt die Hypotenuse in zwei Teile
und
, sodass die beiden Teildreiecke mit den Seiten
,
,
und
,
,
wiederum rechtwinklig sind. Bei Kenntnis zweier der sechs Angaben (
,
,
,
,
und
) lassen sich die fehlenden vier anderen Werte aus den in folgender Tabelle aufgeführten Formeln berechnen.
| Satz des Pythagoras | 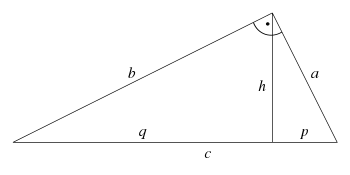 | |
| Kathetensatz | ||
| Höhensatz |
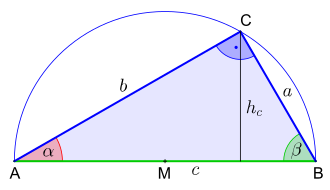
- Der Satz des Thales besagt, dass jedes Dreieck am Halbkreisbogen ein rechtwinkliges Dreieck ist. Der Mittelpunkt der Hypotenuse ist das Zentrum des Thaleskreises, des Umkreises des rechtwinkligen Dreiecks.
- Der Fußpunkt der Höhe teilt die Hypotenuse in zwei Hypotenusenabschnitte. Der Kathetensatz und der Höhensatz machen Aussagen über die Längen dieser Teilstrecken.
- Die trigonometrischen Funktionen beschreiben die rechnerischen Zusammenhänge zwischen den Winkeln und den Seitenverhältnissen.
Berechnung und Konstruktion
Ein rechtwinkliges Dreieck ist durch drei Bestimmungsstücke vollständig bestimmt: den rechten Winkel, eine Seite sowie eine weitere Seite oder einen weiteren Winkel.
- Sind beide Katheten gegeben, so lässt sich das Dreieck nach dem SWS-Fall behandeln.
- Die Kathete
senkrecht auf die Kathete
anordnen. Der Abstand
ergibt die fehlende Hypotenuse
und somit das Dreieck
.
- Sind eine Kathete und die Hypotenuse gegeben, so wird der SSW-Fall angewandt.
- Die Hypotenuse halbieren und über den Mittelpunkt
den Thaleskreis ziehen. Ist z.B. die Kathete
gegeben, schneidet der Kreisbogen um
mit dem Radius
den Thaleskreis in
. Die Verbindung
mit
vollendet das Dreieck
.
- Sind eine Seite und ein nicht-rechter Winkel gegeben, so lässt sich über die Winkelsumme der dritte Winkel bestimmen. Danach kann man das Dreieck nach dem WSW- bzw. SWW-Fall behandeln.
- Ist z.B. die Kathete
und der Winkel
gegeben (WSW-Fall), wird ab
eine gerade Linie gezogen, die mit der Kathete
den Winkel
bildet. Die abschließende Senkrechte auf
ab
schneidet die gerade Linie in
und erzeugt somit das Dreieck
.
- Ist z.B., wie im nebenstehenden Bild zu sehen, die Hypotenuse
und der Winkel
gegeben (SWW-Fall), wird
halbiert und über den Mittelpunkt
der Thaleskreis gezogen. Beim Festlegen des Winkels
mit Scheitel
ergibt sich
auf dem Thaleskreis und damit die Kathete
. Die Verbindung
mit
liefert die Kathete
und vollendet somit das rechtwinklige Dreieck
.
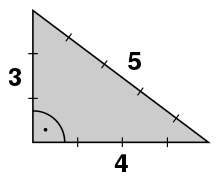
- Stehen im SSS-Fall
die Seiten zueinander im Verhältnis gleich dem eines pythagoreischen
Tripels, beispielsweise
, ist das Dreieck rechtwinklig.
Im rechtwinkligen Dreieck sind die Höhen
und
jeweils gleich den Katheten
bzw.
.
| Mathematische Formeln zum rechtwinkligen Dreieck | ||||
|---|---|---|---|---|
| Flächeninhalt | 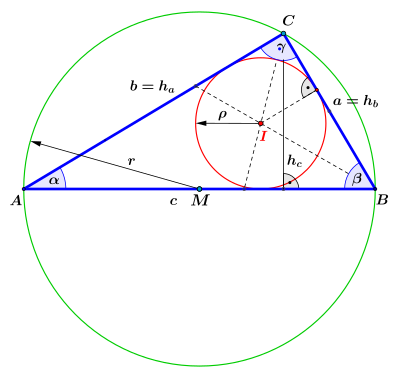 | |||
| Hypotenuse | ||||
| Kathete | ||||
| Umfang | ||||
| Höhe | ||||
| Winkel | ||||
| Inkreisradius | ||||
| Umkreisradius | ||||
Ungleichungen
Für die Katheten
und
gilt
,
also
.
Addition von
ergibt
,
also
.
Nach dem Satz
des Pythagoras folgt daraus
und die Ungleichungen
Die rechte Ungleichung ist ein Spezialfall der Ungleichung vom arithmetischen und geometrischen Mittel.
Division
von
durch die linke Ungleichung
ergibt
.
Wegen
folgt daraus
Aus
folgt wegen
,
,
für die Kehrwerte
,
also
.
Multiplikation mit
auf beiden Seiten ergibt
.
Wegen
folgen daraus die genaueren Ungleichungen
Die Gleichungen
und
gelten genau dann, wenn
,
also für ein rechtwinkliges und gleichschenkliges
Dreieck mit den Innenwinkeln
,
und
.
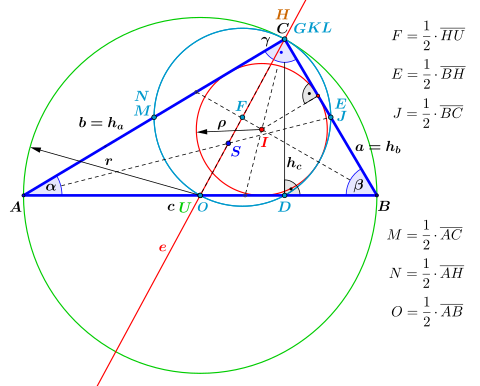
Ausgezeichnete Punkte
Wie aus dem Bild ersichtlich, liegt von den vier „klassischen“ ausgezeichneten
Punkten im rechtwinkligen Dreieck, der Höhenschnittpunkt
(hellbraun) direkt im Scheitel
des rechten Winkles, Eckpunkt
,
und der Umkreismittelpunkt
(hellgrün) in der Mitte der Dreieckseite
Der Schwerpunkt
(dunkelblau) sowie der Inkreismittelpunkt
(rot) sind innerhalb des Dreiecks.
Der Mittelpunkt
des Feuerbachkreises
(beides hellblau) ist in der Mitte der Strecke
und ebenfalls innerhalb des Dreiecks. Auf dem Feuerbachkreis liegen dessen
neun ausgezeichnete Punkte, von denen aber, aufgrund der Position des
Höhenschnittpunktes
nur fünf zu sehen sind. Es sind dies die Seitenmittelpunkte
und
sowie die Höhenfußpunkte
und
Zwei der drei Mittelpunkte der sogenannten oberen Höhenabschnitte,
nämlich
und
liegen auf den Seitenmittelpunkten
bzw.
Der dazugehörende dritte Mittelpunkt
liegt auf dem Scheitelpunkt
Schließlich findet man den dritten Höhenfußpunkt
auf dem Höhenschnittpunkt
Die Bezeichnungen der ausgezeichneten Punkte und deren Positionen sind mit denen des spitzwinkligen Dreiecks vergleichbar.
Die Punkte ,
,
und
befinden sich, wie bei allen Dreiecken, auf der Eulerschen Gerade
(rot).
Satz von Eddy
Der Satz wurde erst im Jahr 1991 formuliert, „ist aber sicher schon sehr viel älter“.
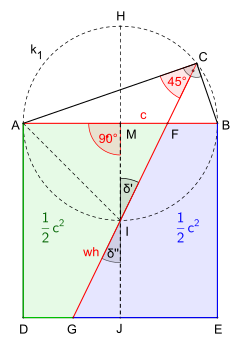
„Die Winkelhalbierende des rechten Winkels eines rechtwinkligen Dreiecks teilt das Hypotenusenquadrat in zwei kongruente Flächen.“
Es sei ein beliebiges Dreieck
mit der Hypotenuse
dem Hypotenusenquadrat
und mit der Winkelhalbierenden
des rechten Winkels am Scheitel
Die Winkelhalbierende
schneidet im Punkt
sowie im Punkt
das Hypotenusenquadrat
in zwei Vierecke
und
Beweise
A) Beweis durch Symmetrie, Bild 1, gleichermaßen der Geometrischer Beweis durch Ergänzung für den Satz des Pythagoras.
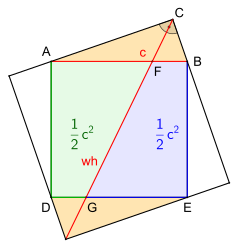
B) Ansatz für einen alternativen Beweis, Bild 2:
- Die beiden Dreiecke
und
müssen kongruent sein.
- Dies trifft nur zu, wenn die Winkelhalbierende
durch den Mittelpunkt des Hypotenusenquadrates
verläuft.
Zuerst wird der Mittelpunkt
der Hypotenuse
bestimmt, anschließend der Kreis
mit dem Radius
um
eingezeichnet und die Mittelsenkrechte des Durchmessers
mit den soeben erzeugten Schnittpunkten
und
eingetragen. Der Schnittpunkt
entspricht dem Mittelpunkt des Hypotenusenquadrates
Abschließend noch den Punkt
mit
verbinden.
Das einbeschriebene Dreieck
hat am Scheitel
den Zentriwinkel mit der Winkelweite gleich
Nach dem Kreiswinkelsatz
(Zentriwinkelsatz) hat der Winkel
folglich die Winkelweite
damit verläuft die Winkelhalbierende
ebenfalls durch den Mittelpunkt
des Hypotenusenquadrates
Somit bestätigt sich, die beiden Dreiecke
und
sind kongruent, demzufolge haben auch die Vierecke
und
gleiche Flächeninhalte.
Siehe auch
- Dreieck
- Gleichseitiges Dreieck
- Gleichschenkliges Dreieck
- Spitzwinkliges Dreieck
- Stumpfwinkliges Dreieck
- Ausgezeichnete Punkte im Dreieck
- Hypotenuse
Anmerkungen
- ↑ Die Bezeichnung „Hypotenuse“ kommt von dem gleichbedeutenden, altgriechischen Begriff ὑποτείνουσα, hypoteinousa, der von: hypo – unter und teinein – spannen, sich erstrecken abgeleitet ist.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.01. 2022