Höhensatz
Der Höhensatz des Euklid, benannt nach Euklid von Alexandria, ist eine Aussage der Elementargeometrie, die in einem rechtwinkligen Dreieck eine Beziehung zwischen der dem rechten Winkel gegenüberliegenden Seite und ihrer zugehörigen Höhe beschreibt. Zusammen mit dem Satz des Pythagoras und dem Kathetensatz bildet er die sogenannte Satzgruppe des Pythagoras.
Satz und Anwendungen
In einem rechtwinkligen Dreieck teilt die zur Hypotenuse gehörige Höhe
diese in zwei Abschnitte
und
,
dabei entspricht die Länge der Höhe dem geometrischen
Mittel der Längen der Abschnitte
und
,
das heißt es gilt:
.
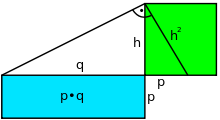
Oft drückt man den Satz auch als Flächen- anstatt als Längenbeziehung aus. In
diesem Fall entspricht dann die Fläche des Höhenquadrats der Fläche des mit den
Hypotenusenabschnitten
und
gebildeten Rechtecks:
.
Letztere Darstellung liefert ein Verfahren zur Quadratur eines
Rechtecks mit Zirkel
und Lineal, das heißt, man kann mit Hilfe des Höhensatzes zu einem gegebenen
Rechteck ein exakt flächengleiches Quadrat nur mit Hilfe von Zirkel und Lineal
konstruieren. Dabei geht man wie folgt vor (siehe dazu auch die Zeichnung
rechts): Zu einem gegebenen Rechteck mit den Seiten
und
bezeichne
einen Eckpunkt. Nun verlängert man in
die Seite
um
,
womit
die neue Strecke
mit der Länge
teilt. Dann zeichnet man einen Halbkreis mit
als Durchmesser und errichtet in
eine Senkrechte zu
,
die den Halbkreis in dem Punkt
schneidet. Nach dem Satz
des Thales formen der Punkt
und der Durchmesser
ein rechtwinkliges Dreieck, dessen Höhenquadrat mit Seitenlänge
flächengleich zum Ausgangsrechteck ist.
Ein weitere Anwendung ist ein geometrischer Beweis der Ungleichung
vom arithmetischen und geometrischen Mittel für zwei Zahlen. Zu den Zahlen
und
konstruiert man einen Halbkreis mit Durchmesser
,
dann entspricht die Höhe dem geometrischen
Mittel und der Radius dem arithmetischen
Mittel. Da nun die Höhe immer kleiner oder gleich dem Radius, hat man somit
die Gültigkeit der Ungleichung gezeigt.
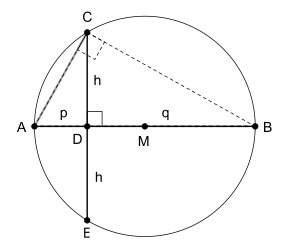
Man kann den Höhensatz auch als einen Spezialfall des Sehnensatzes auffassen. Wenn nämlich die erste Sehne dem Durchmesser des Kreises entspricht und die zweite Sehne senkrecht auf ihr steht, dann entsprechen deren Sehnenabschnitte aufgrund des Satzes von Thales der Höhe in einem rechtwinklingen Dreieck mit der ersten Sehne als Hypotenuse. Zudem sind wegen der Symmetrie des Kreises beide Sehnenabschnitte der zweiten Sehne gleich lang. Damit liefert der Sehnensatz in diesem Fall genau die Gleichung des Höhensatzes.
Es gilt auch die Umkehrung des Höhensatzes. Wenn in einem beliebigen Dreieck
für die Höhe
und die von ihr erzeugten Seitenabschnitte
und
die Beziehung
gilt, so ist das Dreieck rechtwinklig.
Geschichte
Der Höhensatz wird traditionell dem griechischen Mathematiker Euklid zugeschrieben, der ihn in seinen Elementen beschreibt. Dort wird es als Korollar zu Proposition 8 in Buch VI hergeleitet. In Proposition 14 in Buch II gibt Euklid zudem eine Methode zu der Quadrierung eines Rechtecks an, die im Wesentlichen der hier beschriebenen Methode entspricht. Allerdings liefert Euklid dort einen etwas komplizierteren Nachweis für ihre Korrektheit, da er dabei nicht auf den Höhensatz als Beweismittel zurückgreift.
Beweis
Anhand von ähnlichen Dreiecken
Beweis des Satzes:
Die Dreiecke
und
sind ähnlich, da beide ähnlich zum Dreieck
sind. Letzteres ist der Fall, da sie jeweils in zwei Winkeln mit dem Dreieck
übereinstimmen. Die Ähnlichkeit der beiden Dreiecke liefert das folgende
Seitenverhältnis und der Satz ergibt sich einer Äquivalenzumformung der
Verhältnisgleichung:
Beweis der Umkehrung:
Hier ist zu zeigen, dass ein beliebiges Dreieck
mit der Eigenschaft
einen rechten Winkel in
besitzt. Aufgrund der Gleichung für die Höhe gilt auch die folgende
Verhältnisgleichung
.
Damit haben die Dreiecke
and
beiden einen rechten Winkel und stimmen im Seitenverhältnis der an dem rechten
Winkel anliegenden Seiten überein. Also folgt aus Ähnlichkeitssätzen
für Dreiecke (SWS-Satz), dass die beiden Dreiecke ähnlich sind für ähnliche
Dreiecke und es gilt aufgrund der Winkelsumme im Dreieck:
Über Zerlegungen
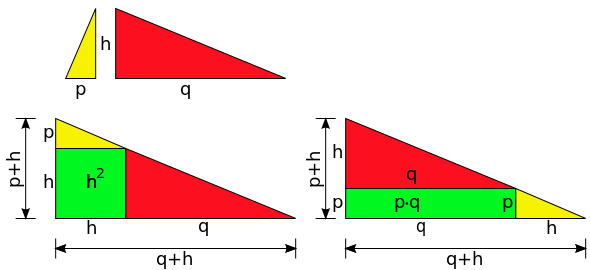
Man schneidet das rechtwinklige Dreieck entlang der Höhe
auf und kann dann die beiden Teildreiecke auf zwei unterschiedliche Arten zu
einem rechtwinkligen Dreieck mit den Katheten
und
arrangieren, bei denen jeweils ein drittes Teilstück fehlt. Im einen Fall hat
das fehlende Teilstück die Fläche
,
im anderen
.
Da beiden fehlenden Stücke die Teildreiecke jeweils zu dem gleichen Dreieck
ergänzen, müssen sie flächengleich sein; das heißt, es gilt
.
Mit dem Satz des Pythagoras
In der Konfiguration des Höhensatzes hat man die drei rechtwinkligen Dreiecke
,
und
,
in denen jeweils der Satz
des Pythagoras gilt. Damit erhält man:
und
und somit auch
.
Division durch zwei liefert dann den Höhensatz.
Über Scherungen
Das Höhenquadrat kann durch drei Scherungen in ein flächengleiches Rechteck mit Seitenlängen p und q überführt werden.



© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2021