Arithmetisches Mittel
Das arithmetische Mittel, auch arithmetischer Mittelwert
genannt (umgangssprachlich auch als Durchschnitt bezeichnet) ist ein
Begriff in der Statistik.
Es ist ein Lageparameter.
Man berechnet diesen Mittelwert,
indem man die Summe der betrachteten Zahlen
durch ihre Anzahl teilt.
Das
arithmetische Mittel einer Stichprobe
wird auch empirischer Mittelwert genannt.
Definition
Die Hälfte der Summe zweier Größen
und
ist gegeben durch:
.
Da die Größen
eine arithmetische
Folge bilden, wird die Merkmalssumme
der Merkmalsausprägungen
dividiert durch die Anzahl der Merkmalsträger
als „arithmetisches Mittel“
(lies:
quer) bezeichnet. Wird das arithmetische Mittel nicht gewichtet (siehe
auch Abschnitt Gewichtetes
arithmetisches Mittel), dann wird es auch als einfaches arithmetisches
Mittel oder ungewichtetes arithmetisches Mittel bezeichnet.
Zum Beispiel ist das arithmetische Mittel der beiden Zahlen
und
:
.
Das arithmetische Mittel beschreibt das Zentrum einer Verteilung durch einen
numerischen Wert und stellt somit einen Lageparameter
dar. Das arithmetische Mittel ist sinnvoll für beliebige metrische Merkmale
definiert. Im Allgemeinen ist es für qualitative Merkmale nicht geeignet, jedoch
liefert es für dichotome Merkmale mit zwei Kategorien
und
eine sinnvolle Interpretation. In diesem Fall ist das arithmetische Mittel
identisch mit der relativen Häufigkeit
.
Gelegentlich wird zur Bezeichnung des arithmetischen Mittels auch das Durchschnittszeichen
ø verwendet. Das arithmetische Mittel ist im Gegensatz zum empirischen Median
sehr anfällig gegenüber Ausreißern (siehe Median).
Das arithmetische Mittel kann als „Mittelpunkt“ der Messwerte interpretiert
werden. Es gibt allerdings keine Auskunft darüber, wie stark die Messwerte um
das arithmetische Mittel streuen. Dieses Problem kann mit der Einführung der
„mittleren quadratischen Abweichung“ vom arithmetischen Mittel, der empirischen Varianz,
behoben werden.
Definition für Häufigkeitsdaten
Für Häufigkeitsdaten
mit den Ausprägungen
und den dazugehörigen relativen
Häufigkeiten
ergibt sich das arithmetische Mittel als
.
Arithmetisches Mittel bei Schichtenbildung
Bei Vorliegen einer geschichteten Stichprobe, deren arithmetischen Mittel in
Schichten bekannt sind, lässt sich das arithmetische Mittel für die
Gesamterhebung berechnen. Es sei eine Erhebungsgesamtheit
mit
Merkmalsträgern in
Schichten
mit der jeweiligen Anzahl an Merkmalsträgern
und arithmetischen Mitteln
eingeteilt. Das arithmetische Mittel
in
ist dann definiert durch
.
Rekursive Darstellung des arithmetischen Mittels
Bei der Betrachtung stationärer
stochastischer Prozesse, bei denen die Daten
in einer zeitlich geordneten Reihenfolge erfasst werden, bietet es sich an, eine
Rekursions-Formel zur
Berechnung des arithmetischen Mittelwertes zu verwenden. Diese lässt sich direkt
anhand der Grundformel des arithmetischen Mittelwertes herleiten. Wie in der
angegebenen Formel ersichtlich werden für kleine
die Daten
stärker gewichtet und für große
der zuvor berechnete arithmetische Mittelwert. Der Vorteil der Rekursions-Formel
ist, dass die Daten
nicht gespeichert werden müssen, was sich z.B. bei Anwendungen auf einem
Microcontroller
anbietet.
Ein erster Schritt, diese rekursive Variante des arithmetischen Mittelwertes
auch für zeitvariable stochastische Prozesse verwendbar zu machen, ist die
Einführung eines sogenannten Vergessens-Faktors .
Zeitvariabel bedeutet hier, dass der tatsächliche Erwartungswert in Abhängigkeit
der Zeit variiert. Typischerweise ist davon auszugehen, dass die Scharmittelwerte den
zeitlichen Mittelwerten entsprechen. Die Einführung des Vergessens-Faktors führt
dazu, dass die Rekursions-Gleichung auf solche Änderungen reagieren kann. Eine
Möglichkeit ist z.B. eine prozentuale Gewichtung des Grenzwertes für
:
Zur Umgehung der rationalen Terme in Abhängigkeit von ,
lässt sich diese Gleichung auch direkt im Grenzwert
wie folgt angeben:
Ob diese Vorgehensweise in einer bestimmten Anwendung praktikabel ist, gilt
es natürlich zu klären. Zu beachten ist, dass sich durch die Verwendung des
Grenzwertes ein anderes "Einschwingverhalten" ergibt. Von systemtheoretischer
(bzw. regelungstechnischer) Warte aus betrachtet, wird eine solche
Rekursionsgleichung auch als zeitdiskretes PT1-Glied
bezeichnet. In der praktischen Umgangssprache würde man den Parameter ,
so wie er hier beschrieben ist, als "Fummel-Faktor" bezeichnen, was zum
Vorschein bringen soll, dass dieser zunächst einmal nicht optimal gewählt ist.
Weiterführend zu diesem Thema sind das Kalman-Filter,
das Wiener-Filter, der rekursive
Least-Square-Algorithmus, das Maximum-Likelihood-Verfahren
und generell Optimalfilter
zu nennen.
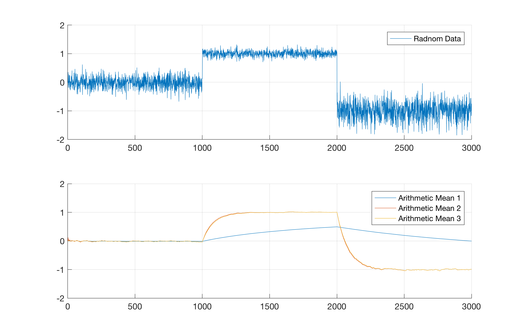
Nebenstehend ist exemplarisch das Verhalten der hier angegebenen
Rekursions-Gleichungen, bei einem einfachen instationären, stochastischen
Prozess (bereichsweise normalverteilt)
zu sehen. Im Verlaufe der Zeit weisen der Erwartungswert sowie die Varianz der
Zufalls-Daten ein sprunghaftes Verhalten auf. Die einfache Rekursionsgleichung
ohne Vergessensfaktor (Arithmetic Mean 1) reagiert nur sehr träge auf das
Verhalten des Datensatzes. Wohingegen die Rekursionsgleichungen mit
Vergessensfaktor (Arithmetic Mean 2 & 3, )
deutlich schneller reagieren. Es fällt weiterhin auf, dass die Algorithmen mit
Vergessensfaktor zu einem etwas größeren Rauschen führen. In diesem Beispiel
sollte jedoch klar sein, dass die schnellere Reaktionszeit Vorrang hat. Die
Ergebnisse "Arithmetic Mean 2" und "Arithmetic Mean 3" unterscheiden sich hier
nur sehr gering voneinander. Je nach Datensatz, vor allem je nach Menge an
Daten, kann dies deutlich anders aussehen.
Eigenschaften
Ersatzwerteigenschaft
Direkt aus der Definition des arithmetischen Mittels folgt, dass
.
Wenn man das arithmetische Mittel mit dem Stichprobenumfang
multipliziert, dann erhält man die Merkmalssumme.
Diese Rechenregel wird als Ersatzwerteigenschaft oder
Hochrechnungseigenschaft bezeichnet und oft bei mathematischen Beweisen
verwendet. Sie kann wie folgt interpretiert werden: Die Summe aller
Einzelwerte kann man sich ersetzt denken durch
gleiche Werte von der Größe des arithmetischen Mittels.
Schwerpunkteigenschaft
Die Abweichungen
der Messwerte
vom Mittelwert
werden auch als „scheinbare Fehler“ bezeichnet. Die Schwerpunkteigenschaft (auch Nulleigenschaft genannt) besagt, dass die Summe der scheinbaren Fehler bzw. die Summe der Abweichungen aller beobachteten Messwerte vom arithmetischen Mittel gleich Null ist, also
beziehungsweise im Häufigkeitsfall
.
Dies lässt sich mithilfe der Ersatzwerteigenschaft wie folgt zeigen:
Die Schwerpunkteigenschaft spielt für das Konzept der Freiheitsgrade
eine große Rolle. Aufgrund der Schwerpunkteigenschaft des arithmetischen Mittels
ist die letzte Abweichung
bereits durch die ersten
bestimmt. Folglich variieren nur
Abweichungen frei und man mittelt deshalb, z.B. bei der empirischen
Varianz, indem man durch die Anzahl
der Freiheitsgrade
dividiert.
Optimalitätseigenschaft
In der Statistik ist man oft daran
interessiert die Summe
der Abweichungsquadrate
von einem Zentrum zu minimieren. Wenn man das Zentrum durch einen Wert
auf der horizontalen Achse festlegen will, der die Summe der quadratischen
Abweichungen
zwischen Daten
und Zentrum
minimiert, dann ist
der minimierende Wert. Dieses Resultat kann durch einfaches Ableiten der
Zielfunktion
nach
gezeigt werden:
.
Dies ist ein Minimum, da die zweite Ableitung von
nach
gleich 2, also größer als 0 ist, was eine hinreichende Bedingung für ein Minimum
ist.
Daraus ergibt sich die folgende Optimalitätseigenschaft (auch Minimierungseigenschaft genannt):
für alle
oder anders ausgedrückt
Lineare Transformationseigenschaft
Je nach Skalenniveau ist das arithmetische Mittel äquivariant gegenüber speziellen Transformationen. Es gilt für die lineare Transformation
,
da
.
Dreiecksungleichungen
Für das arithmetische Mittel gilt die folgende Dreiecksungleichung:
Das arithmetische Mittel von
positiven Merkmalsausprägungen
ist größer oder gleich dem geometrischen
Mittel dieser Merkmalsausprägungen, also
.
Die Gleichheit ist nur gegeben, wenn alle Merkmalsausprägungen gleich sind. Weiterhin gilt für den Absolutbetrag des arithmetischen Mittels mehrerer Merkmalsausprägungen, dass er kleiner oder gleich dem quadratischen Mittel ist
.
Beispiele
Einfache Beispiele
- Das arithmetische Mittel aus 50 und 100 ist
- Das arithmetische Mittel aus 8, 5 und −1 ist
Anwendungsbeispiel
Ein Auto fährt eine Stunde lang 100 km/h und die darauf folgende Stunde 200 km/h. Mit welcher konstanten Geschwindigkeit muss ein anderes Auto fahren, um denselben Weg ebenfalls in zwei Stunden zurückzulegen?
Der Weg ,
den das erste Auto insgesamt zurückgelegt hat, beträgt
und der des zweiten Autos
wobei
die Geschwindigkeit des zweiten Autos ist. Aus
ergibt sich
und damit
Gewichtetes arithmetisches Mittel
Es lässt sich auch ein gewichtetes arithmetisches Mittel definieren (auch als gewogenes arithmetisches Mittel bezeichnet). Es erweitert den Anwendungsbereich des einfachen arithmetischen Mittels auf Werte mit unterschiedlicher Gewichtung. Ein Beispiel ist die Berechnung einer Schulnote, in die mündliche und schriftliche Leistungen unterschiedlich stark einfließen. Bei Anwendung der Richmannsche Mischungsregel zur Bestimmung der Mischtemperatur zweier Körper aus gleichem Material wird ebenfalls ein gewichtetes arithmetisches Mittel berechnet.
Deskriptive Statistik
Das gewichtete Mittel wird beispielsweise verwendet, wenn man Mittelwerte
,
aus
Stichproben der gleichen Grundgesamtheit mit
verschiedenen Stichprobenumfängen
miteinander kombinieren will:
.
Wahrscheinlichkeitsrechnung
Stichprobenmittel
Die konkreten Merkmalausprägungen
lassen sich als Realisierungen
von Zufallsvariablen
auffassen. Jeder
-Wert
stellt somit nach der Ziehung der Stichprobe eine Realisierung der jeweiligen
Zufallsvariablen
dar. Das arithmetische Mittel dieser Zufallsvariablen
wird auch als Stichprobenmittel bezeichnet und ist ebenfalls eine Zufallsvariable.
Inverse Varianzgewichtung
Sind die
unabhängig verteilte Zufallsvariablen (d.h.
ist eine Zufallsvariable mit den Zufallsvariablen
und
ist eine Zufallsvariable mit den Zufallsvariablen
)
mit gemeinsamem Erwartungswert
aber unterschiedlichen Varianzen
,
so hat der gewichtete Mittelwert ebenfalls Erwartungswert
und seine Varianz beträgt
.
Wählt man als Gewicht ,
so vereinfacht sich die Varianz zu
.
Aus der Cauchy-Schwarzschen Ungleichung folgt
.
Die Wahl der Gewichte
oder eine Wahl proportional dazu minimiert also die Varianz
des gewichteten Mittels. Mit dieser Formel lassen sich die Gewichte
abhängig von der Varianz des jeweiligen Wertes, der dementsprechend den
Mittelwert mehr oder weniger stark beeinflusst, zweckmäßig wählen.
Unabhängig und identisch verteilte Zufallsvariablen
Sind
Zufallsvariablen, die
unabhängig
und identisch verteilt mit Erwartungswert
und Varianz
sind, so hat der Stichprobenmittel
ebenfalls den Erwartungswert
,
aber die kleinere Varianz
(siehe Standardfehler).
Hat also eine Zufallsvariable endlichen Erwartungswert und endliche Varianz, so
folgt aus der Tschebyscheff-Ungleichung,
dass das arithmetische Mittel einer Stichprobe gegen den Erwartungswert der
Zufallsvariablen stochastisch
konvergiert. Das arithmetische Mittel ist daher nach vielen Kriterien eine
geeignete Schätzung für den Erwartungswert der Verteilung, aus der die
Stichprobe stammt.
Sind die >
speziell Stichprobenmittelwerte vom Umfang
aus derselben Grundgesamtheit, so hat
die Varianz
,
also ist die Wahl
optimal.
Gewichtetes arithmetisches Mittel als Erwartungswert
Im Falle einer diskreten Zufallsvariable
mit abzählbar endlichem Träger
ergibt sich der Erwartungswert der Zufallsvariable
als
.
Hierbei ist
die Wahrscheinlichkeit,
dass
den Wert
annimmt. Dieser Erwartungswert kann als ein gewichtetes Mittel der Werte
mit den Wahrscheinlichkeiten
interpretiert werden. Bei Gleichverteilung gilt
und somit wird
zum arithmetischen Mittel der Werte
>
.
Beispiele für gewichtete Mittelwerte
Ein Bauer stellt im Nebenerwerb 100 kg Butter her. 10 kg kann er für 10 €/kg verkaufen, weitere 10 kg für 6 €/kg und den Rest muss er für 3 €/kg abgeben. Zu welchem (gewichtetem) Durchschnittspreis hat er seine Butter verkauft? Lösung: (10 kg · 10 €/kg + 10 kg · 6 €/kg + 80 kg · 3 €/kg) / (10 kg + 10 kg + 80 kg) = 400 € / 100 kg = 4 €/kg. Der mit der jeweils verkauften Menge gewichtete Durchschnittspreis entspricht also dem fixen Preis, zu dem die Gesamtmenge verkauft werden müsste, um den gleichen Erlös zu erzielen wie beim Verkauf von Teilmengen zu wechselnden Preisen.
Das arithmetische Mittel
der
Zahlen 1, 2 und 3 beträgt 2, das arithmetische Mittel
der
Zahlen 4 und 5 beträgt 4,5. Das arithmetische Mittel aller 5 Zahlen ergibt sich
als mit dem Stichprobenumfang gewichteter Mittelwert der Teilmittelwerte:
Liegen die Beobachtungen als klassierte Häufigkeit vor, kann man das arithmetische Mittel näherungsweise als gewichtetes Mittel bestimmen, wobei die Klassenmitten als Wert und der Klassenumfang als Gewicht zu wählen sind. Sind beispielsweise in einer Schulklasse ein Kind in der Gewichtsklasse 20 bis 25 kg, 7 Kinder in der Gewichtsklasse 25 bis 30 kg, 8 Kinder in der Gewichtsklasse 30 bis 35 kg und 4 Kinder in der Gewichtsklasse 35 bis 40 kg, so lässt sich das Durchschnittsgewicht als
abschätzen. Um die Güte dieser Schätzung zu ermitteln, muss man dann den minimal / maximal möglichen Mittelwert ermitteln, indem man pro Intervall die kleinsten / größten Werte zugrunde legt. Damit ergibt sich dann, dass der tatsächliche Mittelwert zwischen 28,75 kg und 33,75 kg liegt. Der Fehler der Schätzung 31,25 beträgt also maximal ±2,5 kg oder ±8 %.
Der Mittelwert einer Funktion
Als Mittelwert der Riemann-integrierbaren
Funktion
wird die Zahl
definiert.
Die Bezeichnung Mittelwert ist insofern gerechtfertigt, als für eine
äquidistante Zerlegung
des Intervalls mit der Schrittweite
das arithmetische Mittel
gegen
konvergiert.
Ist
stetig,
so besagt der Mittelwertsatz
der Integralrechnung, dass es ein
gibt mit
,
die Funktion nimmt also an mindestens einer Stelle ihren Mittelwert an.
Der Mittelwert der Funktion
mit dem Gewicht
(wobei
für alle
)
ist
.
Für Lebesgue-Integrale
im Maßraum
mit einem endlichen Maß
lässt sich der Mittelwert einer Lebesgue-integrierbaren Funktion als
definieren. Handelt es sich um einen Wahrscheinlichkeitsraum,
gilt also ,
so nimmt der Mittelwert die Form
an; das entspricht genau dem Erwartungswert
von .
Der Mittelwert einer Funktion hat in Physik und Technik erhebliche Bedeutung insbesondere bei periodischen Funktionen der Zeit, siehe Gleichwert.
Quasi-arithmetischer Mittelwert (f-Mittel)
Sei
eine auf einem reellen Intervall
streng
monotone stetige
(und daher invertierbare) Funktion
und seien
Gewichtsfaktoren. Dann ist für
das mit den Gewichten
gewichtete quasi-arithmetische Mittel definiert als
.
Offensichtlich gilt
Für
erhält man das arithmetische, für
das geometrische
Mittel und für
das
-Potenzmittel.
Dieser Mittelwert lässt sich auf das gewichtete quasi-arithmetische Mittel
einer Funktion
verallgemeinern, wobei
in einem die Bildmenge
von
umfassenden Intervall streng monoton und stetig sei:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.06. 2021