Varianz (Stochastik)

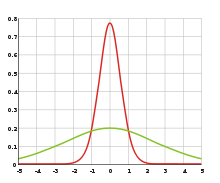
Dichtefunktionen zweier normalverteilter Zufallsvariablen mit gleichem Erwartungswert aber unterschiedlichen Varianzen. Die waagerechte Achse zeigt den Wert, die senkrechte die Häufigkeit.
Die rote Kurve hat eine geringere Varianz (entsprechend der Breite) als die grüne.
Die Quadratwurzel der Varianz, die Standardabweichung, kann bei der Normalverteilung an den Wendepunkten ersehen werden.

In der Stochastik ist die Varianz eine wichtige Kenngröße der Wahrscheinlichkeitsverteilung einer reellen Zufallsvariablen. Sie beschreibt die erwartete quadratische Abweichung der Zufallsvariablen von ihrem Erwartungswert. Damit stellt die Varianz das zweite zentrale Moment der Zufallsvariablen dar. Die Quadratwurzel der Varianz wird Standardabweichung der Zufallsvariablen genannt.

Die Varianz ist translationsinvariant und eine homogene Funktion zweiten Grades. Die Varianz einer Summe unkorrelierter Zufallsvariablen ist gleich der Summe ihrer Varianzen. Ein wichtiges Hilfsmittel zur Berechnung der Varianz stellt der Verschiebungssatz dar. Die Varianz kann mit einem Varianzschätzer, etwa ihrer empirischen Entsprechung, der Stichprobenvarianz, geschätzt werden.

Definition

Es sei eine reelle Zufallsvariable, die integrierbar ist, das heißt, es gilt $\operatorname {E}(|X|)<\infty$ . Dann existiert ihr Erwartungswert $\mu =\operatorname E(X)$ , und man definiert die Varianz von wie folgt:

$\operatorname {Var}(X):=\operatorname {E}\left((X-\mu )^{2}\right).$

Ist quadratisch integrierbar, gilt also $\operatorname {E}(|X|^{2})<\infty$ , so ist die Varianz endlich. Die Varianz wird auch als $\operatorname {V}(X)$ , $\sigma_X^2$ oder einfach als $\sigma ^{2}$ notiert.

Berechnung bei diskreten Zufallsvariablen

Eine reelle Zufallsvariable mit einem endlichen oder abzählbar unendlichen Wertebereich wird diskret genannt. Ihre Varianz berechnet sich dann als

$\operatorname {Var}(X)=\sum _{{x\in A}}(x-\mu )^{2}P(X=x).$

Hierbei ist P(X=x) die Wahrscheinlichkeit, dass den Wert annimmt, und

$\mu =\sum _{{x\in A}}xP(X=x)$

der Erwartungswert von . Die Summen erstrecken sich jeweils über alle Werte, die die Zufallsvariable annehmen kann.

Berechnung bei stetigen Zufallsvariablen

Wenn eine Zufallsvariable eine Wahrscheinlichkeitsdichtefunktion f(x) hat, gilt

$\operatorname {Var}(X)\ =\int _{{-\infty }}^{{\infty }}(x-\mu )^{2}f(x)\,{\mathrm {d}}x,$

wobei

$\mu \ =\int _{{-\infty }}^{{\infty }}xf(x)\,{\mathrm {d}}x.$

Rechenregeln

Verschiebungssatz

Varianzen lassen sich oft einfacher mit Hilfe des Verschiebungssatzes

$\operatorname {Var}(X)=\operatorname {E}\left(\left(X-\operatorname {E}(X)\right)^{2}\right)=\operatorname {E}\left(X^{2}\right)-\left(\operatorname {E}(X)\right)^{2}$

berechnen, da hierzu außer dem Erwartungswert von nur noch der Erwartungswert von $X^{2}$ bestimmt werden muss.
Diskret bedeutet das:

$\operatorname {Var} (X)=\left(\sum _{x\in A}x^{2}P\left(X=x\right)\right)-\left(\sum _{x\in A}xP\left(X=x\right)\right)^{2}$

Am Computer ist diese Art der Berechnung aber zu vermeiden, da es bei der Verwendung von Fließkommazahlen leicht zu katastrophaler Auslöschung kommen kann.

Lineare Transformation

Für reelle Zahlen und gilt

$\operatorname {Var}(aX+b)=a^{2}\operatorname {Var}(X).$

Dies kann mittels des Verschiebungssatzes hergeleitet werden:

${\begin{aligned}\operatorname {Var}(aX+b)&=\operatorname {E}[(aX+b-\operatorname {E}(aX+b))^{2}]\\&=\operatorname {E}[(aX+b-b-a\operatorname {E}(X))^{2}]\\&=\operatorname {E}[a^{2}(X-\operatorname {E}(X))^{2}]\\&=a^{2}\operatorname {E}[(X-\operatorname {E}(X))^{2}]\\&=a^{2}\operatorname {Var}(X)\end{aligned}}$

Insbesondere für a = -1 und b=0 folgt

$\operatorname {Var}(-X)=\operatorname {Var}(X).$

Varianz von Summen von Zufallsvariablen

Für die Varianz einer beliebigen Summe von Zufallsvariablen $X_{1},\dots ,X_{n}$ gilt allgemein

$\operatorname {Var}\left(\sum _{{i=1}}^{n}X_{i}\right)=\sum _{{i,j=1}}^{n}\operatorname {Cov}(X_{i},X_{j})=\sum _{{i=1}}^{n}\operatorname {Var}(X_{i})+\sum _{{i\neq j}}\operatorname {Cov}(X_{i},X_{j})=\sum _{{i=1}}^{n}\operatorname {Var}(X_{i})+2\sum _{{i=1}}^{{n-1}}\sum _{{j=i+1}}^{n}\operatorname {Cov}(X_{i},X_{j}).$

Hierin bezeichnet $\operatorname {Cov}(X_{i},X_{j})$ die Kovarianz der Zufallsvariablen $X_{i}$ und $X_{j}$ und es wurde verwendet, dass $\operatorname {Cov}(X_{i},X_{i})=\operatorname {Var}(X_{i})$ gilt. Speziell für zwei Zufallsvariablen und ergibt sich beispielsweise

$\operatorname {Var}(X+Y)=\operatorname {Var}(X)+\operatorname {Var}(Y)+2\operatorname {Cov}(X,Y).$

Sind die Zufallsvariablen paarweise unkorreliert, das heißt ihre Kovarianzen sind alle gleich Null, dann folgt:

$\operatorname {Var}\left(\sum _{{i=1}}^{n}X_{i}\right)=\sum _{{i=1}}^{n}\operatorname {Var}(X_{i})$

Dieser Satz wird auch als Gleichung von Bienaymé bezeichnet. Er gilt insbesondere dann, wenn die Zufallsvariablen unabhängig sind, denn aus Unabhängigkeit folgt Unkorreliertheit.

Charakteristische Funktion

Die Varianz einer Zufallsvariablen lässt sich auch mit Hilfe ihrer charakteristischen Funktion $\varphi _{{X}}(t)=\operatorname {E}\left(e^{{{\mathrm {i}}tX}}\right)$ darstellen. Wegen $\operatorname {E}(X)={\tfrac {\varphi _{X}'(0)}{{\mathrm {i}}}}$ und $\operatorname {E}(X^{2})=-\varphi _{X}''(0)$ folgt nämlich mit dem Verschiebungssatz

$\operatorname {Var}(X)=\operatorname {E}(X^{2})-(\operatorname {E}(X))^{2}=-\varphi _{X}''(0)-\left({\frac {\varphi _{X}'(0)}{{\mathrm {i}}}}\right)^{{2}}=\left(\varphi _{X}'(0)\right)^{2}-\varphi _{X}''(0).$

Momenterzeugende Funktion

Da für die momenterzeugenden Funktion $M_{X}(t)=\operatorname {E}(e^{{tX}})$ der Zusammenhang

$M_{X}^{{(n)}}(0)=\operatorname {E}(X^{{n}})$

gilt, lässt sich die Varianz damit auf folgende Weise berechnen:

$\operatorname {Var}(X)=\operatorname {E}(X^{2})-(\operatorname {E}(X))^{2}=M_{X}''(0)-\left(M_{X}'(0)\right)^{2}\ .$

Wahrscheinlichkeitserzeugende Funktion

Auch mit der wahrscheinlichkeitserzeugenden Funktion $m_{X}(t)=\operatorname {E}(t^{X})$

lässt sich für diskrete die Varianz berechnen. Es gilt dann

$\operatorname {Var}(X)=\lim _{{t\uparrow 1}}\left(m_{X}''(t)+m_{X}'(t)-m_{X}'(t)^{2}\right)$ ,

falls der linksseitige Grenzwert existiert.

Kumulantenerzeugende Funktion

Die kumulantenerzeugende Funktion einer Zufallsvariable ist definiert als

$g_{X}(t)=\ln \operatorname {E}(e^{{tX}})$ .

Leitet man sie zweimal ab und wertet sie an der Stelle 0 aus, so erhält man die Varianz:

$g''_{X}(t){\bigg |}_{{t=0}}=\operatorname {Var}(X)$ .

Die zweite Kumulante ist also die Varianz.

Varianz einer zusammengesetzten Zufallsvariable

Ist eine zusammengesetzte Zufallsvariable, sprich sind $N,X_{1},X_{2},\dots$ unabhängige Zufallsvariablen und sind die $X_{i}$ identisch verteilt und ist auf $\mathbb{N}_0$ definiert, so lässt sich darstellen als

$Y:=\sum _{{i=1}}^{N}X_{i}$ .

Existieren die zweiten Momente von $N,X_{1},X_{2},\dots$ , so gilt

$\operatorname {Var}(Y)=\operatorname {Var}(N)(\operatorname {E}(X_{1}))^{2}+\operatorname {E}(N)\operatorname {Var}(X_{1})$ .

Diese Aussage ist auch als Blackwell-Girshick-Gleichung bekannt.

Beziehung zur Kovarianz

Die Kovarianz $\operatorname {Cov}(\cdot ,\cdot )$ steht mit der Varianz in folgender Beziehung:

$\operatorname {Cov}(X,X)=\operatorname {Var}(X)$ .

Die folgt direkt aus den Definitionen. Des Weiteren gilt die Cauchy-Schwarzsche Ungleichung

$(\operatorname {Cov}(X,Y))^{2}\leq \operatorname {Var}(X)\operatorname {Var}(Y)$ ,

da die Kovarianz eine positiv semidefinite Bilinearform ist.

Beispiele

Diskrete Zufallsvariable

Gegeben ist eine diskrete Zufallsvariable , welche die Werte , und mit je den Wahrscheinlichkeiten 0{,}5 , 0{,}3 und 0{,}2 annimmt. Der Erwartungswert beträgt

$\operatorname {E}(X)=-1\cdot 0{,}5+1\cdot 0{,}3+2\cdot 0{,}2=0{,}2.$

und die Varianz ist demnach

$\operatorname {Var}(X)=\operatorname {E}{\bigl (}(X-\operatorname {E}(X))^{2}{\bigr )}=(-1-0{,}2)^{2}\cdot 0{,}5+(1-0{,}2)^{2}\cdot 0{,}3+(2-0{,}2)^{2}\cdot 0{,}2=1{,}56.$

Mit dem Verschiebungssatz erhält man ebenfalls

$\operatorname {Var}(X)=\operatorname {E}{\bigl (}X^{2}{\bigr )}-{\bigl (}\operatorname {E}(X){\bigr )}^{2}=(-1)^{2}\cdot 0{,}5+1^{2}\cdot 0{,}3+2^{2}\cdot 0{,}2-0{,}2^{2}=1{,}56.$

Für die Standardabweichung ergibt sich damit

$\sigma _{X}={\sqrt {\operatorname {Var}(X)}}={\sqrt {1{,}56}}\approx 1{,}249.$

Stetige Zufallsvariable

Eine stetige Zufallsvariable habe die Dichtefunktion

$f(x)={\begin{cases}{\frac {1}{x}}&{\text{ falls }}1\leq x\leq e\\0&{\text{ sonst }}\end{cases}}$ .

Mit dem Erwartungswert von

$\operatorname {E}(X)=\int _{1}^{e}x\cdot {\frac {1}{x}}\,dx=e-1$

und dem Erwartungswert von $X^{2}$

$\operatorname {E}{\bigl (}X^{2}{\bigr )}=\int _{{-\infty }}^{\infty }x^{2}\cdot f(x)\,dx=\int _{1}^{e}x^{2}\cdot {\frac {1}{x}}\,dx=\left[{\frac {x^{2}}{2}}\right]_{1}^{e}={\frac {e^{2}}{2}}-{\frac {1}{2}}$

berechnet sich die Varianz mit Hilfe des Verschiebungssatzes als

$\operatorname {Var}(X)=\operatorname {E}{\bigl (}X^{2}{\bigr )}-{\bigl (}\operatorname {E}(X){\bigr )}^{2}={\frac {e^{2}}{2}}-{\frac {1}{2}}-(e-1)^{2}\approx 0{,}242.$

Verallgemeinerungen

Im Falle eines reellen Zufallsvektors $X=(X_{1},\dots ,X_{n})^{T}$ mit quadratisch integrierbaren Komponenten verallgemeinert sich die Varianz zu der Kovarianzmatrix eines Zufallsvektors:

$\operatorname {Cov}(X):=\operatorname E\left((X-\mu )(X-\mu )^{T}\right).$

Dabei ist $\mu =\operatorname {E} (X)=(\operatorname {E} (X_{1}),\dots ,\operatorname {E} (X_{n}))^{T}$ der Vektor der Erwartungswerte. Der Eintrag der -ten Zeile und -ten Spalte der Kovarianzmatrix ist $\operatorname {Cov}(X_{i},X_{j})$ . In der Diagonale stehen also die Varianzen $\operatorname {Var}(X_{i})=\operatorname {Cov}(X_{i},X_{i})$ der einzelnen Komponenten.

Analog zu bedingten Erwartungswerten lassen sich beim Vorliegen von Zusatzinformationen, wie beispielsweise den Werten einer weiteren Zufallsvariablen, bedingte Varianzen betrachten.

Basierend auf einem Artikel in:

Wikipedia.de