Standardabweichung

Die Standardabweichung ist ein um 1860 von Francis Galton eingeführter Begriff der Statistik und der Wahrscheinlichkeitsrechnung und ein Maß für die Streuung der Werte einer Zufallsvariablen um ihren Erwartungswert. Sie ist für eine Zufallsvariable definiert als die Quadratwurzel aus deren Varianz und wird als $\sigma_X = \sqrt{\operatorname{Var}(X)}$ notiert.

Liegt eine Beobachtungsreihe $(x_1, x_2, \dots, x_N)$ der Länge vor, so sind empirischer Mittelwert und empirische Standardabweichung zwei wichtige Maßzahlen in der Statistik zur Beschreibung der Eigenschaften der Beobachtungsreihe.

Die Standardabweichung besitzt die gleiche Dimension wie die Messwerte der Beobachtungsreihe. Die Dimension der Varianz ist dagegen das Quadrat der Dimension der Beobachtungswerte.

Als Abkürzung findet man neben $\sigma$ (sprich: „Sigma“) in Anwendungen insbesondere für die empirische Standardabweichung oft s oder SD (für englisch standard deviation), sowie m. F. für mittlerer Fehler. In der angewandten Statistik findet man häufig die Kurzschreibweise der Art „ø 21 ± 4“, was als „Mittelwert 21 mit einer Standardabweichung von 4“ zu lesen ist. (Das Plusminuszeichen wird auch bei der Angabe von Toleranzen oder von Streuintervallen verwendet.)

Definition

Die Standardabweichung $\sigma _{X}$ einer Zufallsvariablen ist definiert als die Quadratwurzel der Varianz $\operatorname{Var}(X)$ :

$\sigma_X := \sqrt{\operatorname{Var}(X)}.$

Dabei ist die Varianz

$\operatorname{Var}(X) = \operatorname E((X-\operatorname E(X))^2) = \operatorname E(X^2) - (\operatorname{E}(X))^2$

stets größer oder gleich 0. Das Symbol $\operatorname E(\cdot)$ bezeichnet den Erwartungswert.

Beispiele und Faustformeln

Normalverteilung

Eindimensionale Normalverteilungen werden durch Angabe von Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ vollständig beschrieben. Ist also eine $\mu$ - $\sigma ^{2}$ -verteilte Zufallsvariable – in Symbolen $X \sim \mathcal{N}(\mu,\sigma^2)$ –, so ist ihre Standardabweichung einfach $\sigma_X = \sqrt{\sigma^2} = \sigma$ .

Streuintervalle

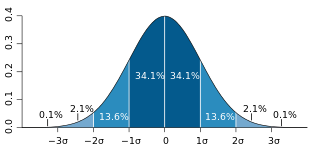
Intervalle um $\mu$ bei der Normalverteilung

Aus der Tabelle der Standardnormalverteilung ist ersichtlich, dass für normalverteilte Zufallsgrößen jeweils ungefähr

68,3 % der Realisierungen im Intervall $\mu\pm\sigma$ ,

95,4 % im Intervall $\mu\pm 2\sigma$ und

99,7 % im Intervall $\mu\pm 3\sigma$

liegen. Da in der Praxis viele Zufallsgrößen annähernd normalverteilt sind, werden diese Werte aus der Normalverteilung oft als Faustformel benutzt. So wird beispielsweise σ oft als die halbe Breite des Intervalls angenommen, welches die mittleren zwei Drittel der Werte in einer Stichprobe umfasst.

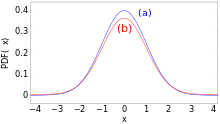
Normalverteilung (a) und kontaminierte Normalverteilung (b)

Diese Praxis ist aber nicht empfehlenswert, denn sie kann zu sehr großen Fehlern führen. Zum Beispiel ist die Verteilung $P=0{,}9\cdot {\mathcal {N}}(\mu ,\sigma ^{2})+0{,}1\cdot {\mathcal {N}}(\mu ,(10\sigma )^{2})$ optisch kaum von der Normalverteilung zu unterscheiden (siehe Bild), aber bei ihr liegen im Intervall $\mu \pm {\bar {\sigma }}$ 92,5 % der Werte, wobei ${\bar \sigma }$ die Standardabweichung von bezeichnet. Solche kontaminierten Normalverteilungen sind in der Praxis sehr häufig; das genannte Beispiel beschreibt die Situation, wenn zehn Präzisionsmaschinen etwas herstellen, aber eine davon schlecht justiert ist und zehnmal weniger präzise als die anderen neun produziert.

Werte außerhalb der zwei- bis dreifachen Standardabweichung werden oft als Ausreißer behandelt. Ausreißer können ein Hinweis auf grobe Fehler der Datenerfassung sein. Es kann den Daten aber auch eine stark schiefe Verteilung zu Grunde liegen. Andererseits liegt bei einer Normalverteilung im Durchschnitt ca. jeder 20. Messwert außerhalb der zweifachen Standardabweichung und ca. jeder 500. Messwert außerhalb der dreifachen Standardabweichung.

Da der Anteil der Werte außerhalb der sechsfachen Standardabweichung mit ca. 2 ppb verschwindend klein wird, gilt ein solches Intervall als gutes Maß für eine nahezu vollständige Abdeckung aller Werte. Das wird im Qualitätsmanagement durch die Methode Six Sigma genutzt, indem die Prozessanforderungen Toleranzgrenzen von mindestens 6σ vorschreiben. Allerdings geht man dort von einer langfristigen Mittelwertverschiebung um 1,5 Standardabweichungen aus, so dass der zulässige Fehleranteil auf 3,4 ppm steigt. Dieser Fehleranteil entspricht einer viereinhalbfachen Standardabweichung (4,5σ). Ein weiteres Problem der 6σ-Methode ist, dass die 6σ-Punkte praktisch nicht bestimmbar sind. Bei unbekannter Verteilung (d.h. wenn es sich nicht ganz sicher um eine Normalverteilung handelt) grenzen zum Beispiel die Extremwerte von 1.400.000.000 Messungen ein 75%-Konfidenzintervall für die 6σ-Punkte ein.

Abhängigkeit der Wahrscheinlichkeit (Prozent innerhalb) von der Größe des Streuintervalls p(z)

Abhängigkeit der Streuintervallgrenze von der eingeschlossenen Wahrscheinlichkeit z(p)

Erwartete Anteile der Werte einer normalverteilten Zufallsvariablen innerhalb bzw. außerhalb der Streuintervalle (μ−zσ, μ+zσ)
zσ	Prozent innerhalb	Prozent außerhalb	ppb außerhalb	Bruchteil außerhalb
0,674 490σ	50%	50%	500.000.000 ppb	1 / 2
0,994 458σ	68%	32%	320.000.000 ppb	1 / 3,125
1σ	68,268 9492%	31,731 0508%	317.310.508 ppb	1 / 3,151 4872
1,281 552σ	80%	20%	200.000.000 ppb	1 / 5
1,644 854σ	90%	10%	100.000.000 ppb	1 / 10
1,959 964σ	95%	5%	50.000.000 ppb	1 / 20
2σ	95,449 9736%	4,550 0264%	45.500.264 ppb	1 / 21,977 895
2,575 829σ	99%	1%	10.000.000 ppb	1 / 100
3σ	99,730 0204%	0,269 9796%	2.699.796 ppb	1 / 370,398
3,290 527σ	99,9%	0,1%	1.000.000 ppb	1 / 1.000
3,890 592σ	99,99%	0,01%	100.000 ppb	1 / 10.000
4σ	99,993 666%	0,006 334%	63.340 ppb	1 / 15.787
4,417 173σ	99,999%	0,001%	10.000 ppb	1 / 100.000
4,891 638σ	99,9999%	0,0001%	1.000 ppb	1 / 1.000.000
5σ	99,999 942 6697%	0,000 057 3303%	573,3303 ppb	1 / 1.744.278
5,326 724σ	99,999 99%	0,000 01%	100 ppb	1 / 10.000.000
5,730 729σ	99,999 999%	0,000 001%	10 ppb	1 / 100.000.000
6σ	99,999 999 8027%	0,000 000 1973%	1,973 ppb	1 / 506.797.346
6,109 410σ	99,999 9999%	0,000 0001%	1 ppb	1 / 1.000.000.000
6,466 951σ	99,999 999 99%	0,000 000 01%	0,1 ppb	1 / 10.000.000.000
6,806 502σ	99,999 999 999%	0,000 000 001%	0,01 ppb	1 / 100.000.000.000
7σ	99,999 999 999 7440%	0,000 000 000 256%	0,002 56 ppb	1 / 390.682.215.445

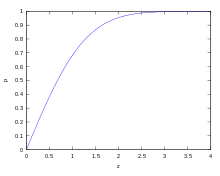
Die Wahrscheinlichkeiten für bestimmte Streuintervalle $[\mu -z\sigma ;\mu +z\sigma ]$ können berechnet werden als

$p=2\Phi (z)-1$ ,

wobei $\Phi (z)={\frac {1}{{\sqrt {2\pi }}}}\int _{{-\infty }}^{z}e^{{-{\frac {x^{2}}{2}}}}\,dx$ die Verteilungsfunktion der Standardnormalverteilung ist.

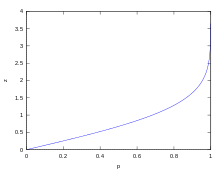
Umgekehrt können für gegebenes $p\in (0,1)$ durch

$z=\Phi ^{{-1}}\left({\frac {p+1}{2}}\right)$

die Grenzen des zugehörigen Streuintervalls $[\mu -z\sigma ;\mu +z\sigma ]$ mit Wahrscheinlichkeit berechnet werden.

Ein Beispiel (mit Schwankungsbreite)

Die Körpergröße des Menschen ist näherungsweise normalverteilt. Bei einer Stichprobe von 1.284 Mädchen und 1.063 Jungen zwischen 14 und 18 Jahren wurde bei den Mädchen eine durchschnittliche Körpergröße von 166,3 cm (Standardabweichung 6,39 cm) und bei den Jungen eine durchschnittliche Körpergröße von 176,8 cm (Standardabweichung 7,46 cm) gemessen.

Demnach lässt obige Schwankungsbreite erwarten, dass 68,3 % der Mädchen eine Körpergröße im Bereich 166,3 cm ± 6,39 cm und 95,4 % im Bereich 166,3 cm ± 12,78 cm haben,

16 % [≈ (100 % − 68,3 %)/2] der Mädchen kleiner als 160 cm (und 16 % entsprechend größer als 173 cm) sind und
2,5 % [≈ (100 % − 95,4 %)/2] der Mädchen kleiner als 154 cm (und 2,5 % entsprechend größer als 179 cm) sind.

Für die Jungen lässt sich erwarten, dass 68 % eine Körpergröße im Bereich 176,8 cm ± 7,46 cm und 95 % im Bereich 176,8 cm ± 14,92 cm haben,

16 % der Jungen kleiner als 169 cm (und 16 % größer als 184 cm) und
2,5 % der Jungen kleiner als 162 cm (und 2,5 % größer als 192 cm) sind.

Diskrete Gleichverteilung, Würfel

Die diskrete Gleichverteilung auf den Zahlen $1,\dots,n$ hat einen Erwartungswert von $m = \tfrac{n+1}{2}$ und eine Standardabweichung von $\sigma = \sqrt{\tfrac{n^2-1}{12}}$ . Das Ergebnis des Wurfes eines fairen sechsseitigen Würfels hat also beispielsweise den Erwartungswert 3,5 und eine Standardabweichung von etwa 1,7.

Binomialverteilung

Ist binomialverteilt mit Parametern (Anzahl der Wiederholungen) und (Erfolgswahrscheinlichkeit), so gilt $\operatorname{E}(X) = np$ und $\operatorname{Var}(X) = n p (1-p)$ , also $\sigma_X = \sqrt{n p (1-p)}.$

Würfelt man beispielsweise 500 Mal mit einem fairen Würfel, so ist die Anzahl der Einser binomialverteilt mit n=500 und $p=\tfrac{1}{6}$ . Der Erwartungswert beträgt

$\mu=np=\frac{500}{6}\approx 83{,}3$

und die Standardabweichung

$\sigma = \sqrt{np(1-p)}= \sqrt{ 500 \cdot \frac{1}{6} \cdot \frac{5}{6}}\approx 8{,}3.$

Weil eine Binomialverteilung mit den obigen Parametern nähernd normalverteilt ist, lassen die Faustformeln also erwarten, dass in 68 % der Fälle die Anzahl der Einser zwischen 75 und 92 liegt und in 95 % der Fälle zwischen 67 und 100.

Schätzung der Standardabweichung der Grundgesamtheit aus einer Stichprobe

Allgemeiner Fall

Berechnungsgrundlagen

Sind die Zufallsvariablen $X_{i}$ unabhängig und identisch verteilt, also beispielsweise eine Stichprobe, so wird die Standardabweichung der Grundgesamtheit der Stichprobe häufig mit der Formel

$S={\sqrt {S^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{{i=1}}^{n}{(X_{i}-{\bar {X}})^{2}}}}$

geschätzt. Dabei ist

die Schätzfunktion für die Standardabweichung $\sigma _{X}$ der Grundgesamtheit
der Stichprobenumfang (Anzahl der Werte)
$X_{i}$ die Merkmalsausprägung am -ten Element der Stichprobe
$\bar{X}= \frac{1}{n} \sum_{i=1}^n{X_i}$ der empirische Mittelwert, also das arithmetische Mittel der Stichprobe.

Diese Formel erklärt sich daraus, dass die korrigierte Stichprobenvarianz $S^{2}$ ein erwartungstreuer Schätzer für die Varianz $\sigma_X^2$ der Grundgesamtheit ist. Im Gegensatz dazu ist aber kein erwartungstreuer Schätzer für die Standardabweichung. Da die Quadratwurzel eine konkave Funktion ist, folgt aus der Jensenschen Ungleichung

$\operatorname{E}(S) = \operatorname{E}\left(\sqrt {S^2}\right) \leq \sqrt{\operatorname{E}\left(S^2 \right)} = \sigma_X$ .

Dieser Schätzer unterschätzt also in den meisten Fällen die Standardabweichung der Grundgesamtheit.

Beispiel

Wählt man eine der Zahlen oder durch Wurf einer fairen Münze, also beide mit Wahrscheinlichkeit jeweils ${\tfrac {1}{2}}$ , so ist das eine Zufallsgröße mit Erwartungswert 0, Varianz $\sigma^2=1$ und Standardabweichung $\sigma =1$ . Berechnet man aus n=2 unabhängigen Würfen $X_{1}$ und $X_{2}$ die korrigierte Stichprobenvarianz

$S^2=\frac 1{2-1}\left(\left(X_1-\bar X\right)^2+\left(X_2-\bar X\right)^2\right),$

wobei

$\bar X=\frac{X_1+X_2}2$

den Stichprobenmittelwert bezeichnet, so gibt es vier mögliche Versuchsausgänge, die alle jeweils Wahrscheinlichkeit 1/4 haben:

${\bar {X}}$	$S^{2}$
	$0$	$0$
$0$		${\sqrt {2}}$
$0$		${\sqrt {2}}$
	$0$	$0$

Der Erwartungswert der korrigierten Stichprobenvarianz beträgt daher

$\operatorname{E}\left(S^2\right) = \frac{0+2+2+0}4 = 1 = \sigma^2$ .

Die korrigierte Stichprobenvarianz ist demnach also tatsächlich erwartungstreu. Der Erwartungswert der korrigierten Stichprobenstandardabweichung beträgt hingegen

$\operatorname{E}(S)= \frac{0 + \sqrt 2 + \sqrt 2 + 0}4 = \frac{\sqrt 2}2 < 1 = \sigma$ .

Die korrigierte Stichprobenstandardabweichung unterschätzt also die Standardabweichung der Grundgesamtheit.

Berechnung für auflaufende Messwerte

In Systemen, die kontinuierlich große Mengen an Messwerten erfassen, ist es oft unpraktisch, alle Messwerte zwischenzuspeichern, um die Standardabweichung zu berechnen.

In diesem Zusammenhang ist es günstiger, eine modifizierte Formel zu verwenden, die den kritischen Term $\textstyle \sum _{{i=1}}^{n}{(x_{i}-{\bar {x}})^{2}}$ umgeht. Dieser kann nicht für jeden Messwert sofort berechnet werden, da der Mittelwert ${\bar {x}}$ nicht konstant ist.

Durch Anwendung des Verschiebungssatzes und der Definition des Mittelwerts $\textstyle {\bar {x}}={\frac {1}{n}}\sum _{{i=1}}^{n}{x_{i}}$ gelangt man zur Darstellung

$\begin{align} s & = {} \sqrt{\frac{1}{n-1} \left[\left(\sum_{i=1}^n x_i^2\right) - \frac{1}{n}\left(\sum_{i=1}^n x_i\right)^2\right]} \end{align}$

die sich für jeden eintreffenden Messwert sofort aktualisieren lässt, wenn die Summe der Messwerte $\textstyle \sum _{{i=1}}^{n}{x_{i}}$ sowie die Summe ihrer Quadrate $\textstyle \sum _{{i=1}}^{n}{x_{i}^{2}}$ mitgeführt und fortlaufend aktualisiert werden. Diese Darstellung ist allerdings numerisch weniger stabil, insbesondere kann der Term unter der Quadratwurzel numerisch durch Rundungsfehler kleiner als 0 werden.

Normalverteilte Zufallsgröße

Berechnungsgrundlagen

Für den Fall normalverteilter Zufallsgrößen lässt sich allerdings ein erwartungstreuer Schätzer angeben:

${\sqrt {\frac {n-1}{2}}}\ {\frac {\Gamma \left({\frac {n-1}{2}}\right)}{\Gamma \left({\frac {n}{2}}\right)}}S$

Dabei ist die Schätzung der Standardabweichung und $\Gamma (x)$ die Gammafunktion. Die Formel folgt indem man beachtet, dass ${\frac {(n-1)S^{2}}{\sigma ^{2}}}$ eine Chi-Quadrat-Verteilung mit n-1 Freiheitsgraden hat.

Korrekturfaktoren für die erwartungstreue Schätzung der Standardabweichung
Stichprobenumfang	Korrekturfaktor
2	1,253314
5	1,063846
10	1,028109
15	1,018002
25	1,010468

Beispiel

Es wurden bei einer Stichprobe aus einer normalverteilten Zufallsgröße die fünf Werte 3, 4, 5, 6, 7 gemessen. Man soll nun die Schätzung für die Standardabweichung errechnen.

Der Stichprobenvarianz ist:

$s_X^2=\tfrac 14(2^2+1^2+0+1^2+2^2)=2{,}5$

Der Korrekturfaktor ist in diesem Fall

$\sqrt{2} \ \frac{\Gamma\left(2\right)}{\Gamma\left(2{,}5\right)} \approx 1{,}063846$

und die erwartungstreue Schätzung für die Standardabweichung ist damit näherungsweise

$\hat{\sigma} =1{,}064 \sqrt{2{,}5}=1{,}68$

Basierend auf einem Artikel in:

Wikipedia.de