Erwartungstreue

Erwartungstreue (selten Unverzerrtheit, englisch unbiasedness) bezeichnet in der mathematischen Statistik eine Eigenschaft einer Schätzfunktion (kurz: eines Schätzers). Ein Schätzer heißt erwartungstreu, wenn sein Erwartungswert gleich dem wahren Wert des zu schätzenden Parameters ist. Ist eine Schätzfunktion nicht erwartungstreu, spricht man davon, dass der Schätzer verzerrt ist. Das Ausmaß der Abweichung seines Erwartungswerts vom wahren Wert nennt man Verzerrung oder Bias. Das Bias drückt den systematischen Fehler des Schätzers aus.

Erwartungstreue zählt neben Konsistenz, Suffizienz und (asymptotischer) Effizienz zu den vier gebräuchlichen Kriterien zur Beurteilung der Qualität von Schätzern. Des Weiteren gehört sie gemeinsam mit der Suffizienz und der Invarianz/Äquivarianz zu den typischen Reduktionsprinzipien der mathematischen Statistik.

Bedeutung

Die Erwartungstreue ist eine wichtige Eigenschaft eines Schätzers, da die Varianz der meisten Schätzer mit steigendem Stichprobenumfang gegen Null konvergiert. D.h. die Verteilung zieht sich um den Erwartungswert des Schätzers, und damit bei erwartungstreuen Schätzern um den gesuchten wahren Parameter der Grundgesamtheit, zusammen. Bei erwartungstreuen Schätzern können wir erwarten, dass die Differenz zwischen dem aus der Stichprobe berechneten Schätzwert und dem wahren Parameter umso kleiner ist, je größer der Stichprobenumfang ist.

Außer zur praktischen Beurteilung der Qualität von Schätzern ist der Begriff der Erwartungstreue auch für die mathematische Schätztheorie von großer Bedeutung. In der Klasse aller erwartungstreuen Schätzer gelingt es – unter geeigneten Voraussetzungen an das zugrundeliegende Verteilungsmodell –, Existenz und Eindeutigkeit bester Schätzer zu beweisen. Das sind erwartungstreue Schätzer, die unter allen möglichen erwartungstreuen Schätzern minimale Varianz haben.

Grundidee und einführende Beispiele

Um einen unbekannten reellen Parameter $\gamma$ einer Grundgesamtheit zu schätzen, berechnet man in der mathematischen Statistik aus einer zufälligen Stichprobe $X_{1},\dotsc ,X_{n}$ mit Hilfe einer geeignet gewählten Funktion eine Schätzung $g(X_{1},\dotsc ,X_{n})$ . Allgemein lassen sich geeignete Schätzfunktionen mit Hilfe von Schätzmethoden, z.B. der Maximum-Likelihood-Methode, gewinnen.

Da die Stichprobenvariablen $X_{1},\dotsc ,X_{n}$ Zufallsvariablen sind, ist auch der Schätzer $g(X_{1},\dotsc ,X_{n})$ selbst eine Zufallsvariable. Er wird erwartungstreu genannt, wenn der Erwartungswert dieser Zufallsvariable stets gleich dem Parameter $\gamma$ ist, egal welchen Wert $\gamma$ in Wirklichkeit hat.

Beispiel Stichprobenmittel

Zur Schätzung des Erwartungswertes $\gamma =\mu$ der Grundgesamtheit wird üblicherweise das Stichprobenmittel

$g(X_{1},\dotsc ,X_{n})=\overline {X}_{n}={\frac {1}{n}}\sum _{{i=1}}^{{n}}X_{i}$

verwendet. Werden alle Stichprobenvariablen $X_{i}$ zufällig aus der Grundgesamtheit gezogen, so haben alle den Erwartungswert $\operatorname {E} (X_{i})=\mu$ . Damit berechnet sich der Erwartungswert des Stichprobenmittels zu

$\operatorname {E} ({\overline {X}}_{n})=\operatorname {E} \left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n}}\sum _{i=1}^{n}\operatorname {E} (X_{i})={\frac {1}{n}}\cdot n\cdot \mu =\mu$ .

Das Stichprobenmittel ist also ein erwartungstreuer Schätzer des unbekannten Verteilungsparameters $\mu$ .

Verteilung des Schätzers $\overline {X}_{n}$ für verschiedene Stichprobenumfänge .

Falls die Grundgesamtheit normalverteilt ist mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ , dann lässt sich die Verteilung von $\overline {X}_{n}$ genau angeben. In diesem Fall gilt

${\overline {X}}_{n}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n),$

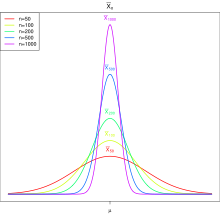
das heißt, das Stichprobenmittel ist ebenfalls normalverteilt mit Erwartungswert $\mu$ und Varianz ${\tfrac {\sigma ^{2}}{n}}$ . Ist der Stichprobenumfang groß, so gilt aufgrund des zentralen Grenzwertsatzes diese Verteilungsaussage zumindest näherungsweise, auch wenn die Grundgesamtheit nicht normalverteilt ist. Die Varianz dieses Schätzers konvergiert also gegen 0, wenn der Stichprobenumfang gegen unendlich geht. Die Grafik rechts zeigt, wie sich für verschiedene Stichprobenumfänge die Verteilung der Stichprobenmittel immer weiter auf einen festen Wert zusammenzieht. Aufgrund der Erwartungstreue ist sichergestellt, dass dieser Wert der gesuchte Parameter $\mu$ ist.

Beispiel relative Häufigkeit

Um zu schätzen, mit welcher Wahrscheinlichkeit ein bestimmtes Merkmal in der Grundgesamtheit auftritt, wird daraus eine Stichprobe von Umfang zufällig ausgewählt und die absolute Häufigkeit > des Merkmals in der Stichprobe ausgezählt. Die Zufallsvariable ist dann binomialverteilt mit den Parametern und , insbesondere gilt für ihren Erwartungswert $\operatorname {E} (X)=np$ . Für die relative Häufigkeit

$h_{n}={\frac {X}{n}}$

folgt dann $\operatorname {E} (h_{n})={\tfrac {1}{n}}\operatorname {E} (X)={\tfrac {np}{n}}=p,$ das heißt, sie ist ein erwartungstreuer Schätzer der unbekannten Wahrscheinlichkeit .

Definition

In der modernen, maßtheoretisch begründeten mathematischen Statistik wird ein statistisches Experiment durch ein statistisches Modell $({\mathcal {X}},{\mathcal {F}},P_{\vartheta }:\vartheta \in \Theta )$ beschrieben. Dieses besteht aus einer Menge ${\mathcal {X}}$ , dem Stichprobenraum, zusammen mit einer σ-Algebra ${\mathcal {F}}$ und einer Familie $(P_{\vartheta })_{\vartheta \in \Theta }$ von Wahrscheinlichkeitsmaßen auf ${\mathcal {X}}$ .

Es sei ein Punktschätzer

$T\colon {\mathcal {X}}\to \mathbb {R}$

sowie eine zu schätzende Funktion

$\gamma \colon \Theta \to \mathbb{R}$

gegeben (im parametrischen Fall die sogenannte Parameterfunktion), die jeder Wahrscheinlichkeitsverteilung $P_{\vartheta }$ die zu schätzende Kennzahl $g(\vartheta )$ (Varianz, Median, Erwartungswert etc.) zuordnet.

Dann heißt der Schätzer erwartungstreu, wenn

$\operatorname {E} _{\vartheta }(T)=\gamma (\vartheta )$

für alle $\vartheta \in \Theta$ ist. Hierbei bezeichnet $\operatorname {E} _{\vartheta }$ den Erwartungswert bezüglich des Wahrscheinlichkeitsmaßes $P_{\vartheta }$ .

In Anwendungen ist $P_{\vartheta }$ oft die Verteilung einer (reellen oder vektorwertigen) Zufallsvariable $X\colon \Omega \to {\mathcal {X}}$ auf einem Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,Q)$ mit einem unbekannten Parameter oder Parametervektor $\vartheta$ . Ein Schätzer für $\gamma (\vartheta )$ ist dann gegeben durch eine Funktion g(X) und diese heißt analog erwartungstreu, wenn gilt

$\operatorname {E} (g(X))=\gamma (\vartheta ),$

wobei der Erwartungswert nun bezüglich gebildet wird.

Eigenschaften

Existenz

Erwartungstreue Schätzer müssen im Allgemeinen nicht existieren. Wesentlich hierfür ist die Wahl der Funktion $g(\vartheta )$ . So kann bei unpassender Wahl der zu schätzenden Funktion die Menge der erwartungstreuen Schätzer klein sein, unsinnige Eigenschaften aufweisen oder leer sein.

Im Binomial-Modell

$X=\{0,1,\dots ,n\},\;{\mathcal {A}}={\mathcal {P}}(X),\;P_{\vartheta }=\operatorname {Bin} _{n,\vartheta }{\text{ für }}\vartheta \in [0,1]$

sind beispielsweise nur Polynome in $\vartheta$ von Grad kleinergleich n erwartungstreu schätzbar. Für zu schätzende Funktionen, die nicht von der Form

$g(\vartheta )=a_{n}\vartheta ^{n}+a_{n-1}\vartheta ^{n-1}+\dots +a_{1}\vartheta +a_{0}$

sind existiert also kein erwartungstreuer Schätzer.

Im Poisson-Modell

$X=\mathbb {N} ,\;{\mathcal {A}}={\mathcal {P}}(\mathbb {N} ),\;P_{\vartheta }=\operatorname {Poi} _{\vartheta }{\text{ für }}\vartheta \in (0,\infty )$

und bei Verwendung der zu schätzenden Funktion

$g(\vartheta )=\exp(-3\vartheta )$

ergibt sich als einziger erwartungstreuer Schätzer

$T(k)=(-2)^{k}{\text{ für }}k\in \mathbb {N}$ .

Dieser Schätzer ist augenscheinlich sinnlos. Zu beachten ist hier, dass die Wahl der zu schätzenden Funktion nicht exotisch ist: Sie schätzt die Wahrscheinlichkeit, dass dreimal in Folge (bei unabhängiger Wiederholung) kein Ereignis eintritt.

Struktur

Gegeben sei ein fixes statistisches Modell. Sei $D_{g}$ die Menge der erwartungstreuen Schätzer für die zu schätzende Funktion und $D_{0}$ die Menge aller Nullschätzer, also

$D_{0}=\{T\,|\,\operatorname {E} _{\vartheta }(T)=0{\text{ für alle }}\vartheta \in \Theta \}$ .

Wählt man nun ein $T\in D_{g}$ aus, so ist

$D_{g}=T+D_{0}$ .

Die Menge aller erwartungstreuen Schätzer für entstehen demnach aus einem erwartungstreuen Schätzer für in Kombination mit den Nullschätzern.

Beziehung zu Verzerrung und MQF

Erwartungstreue Schätzer haben per Definition eine Verzerrung von Null:

$\operatorname {Bias} _{\vartheta }(T):=\operatorname {E} _{\vartheta }(T)-g(\vartheta )=0{\text{ für alle }}\vartheta \in \Theta$ .

Damit reduziert sich der mittlere quadratische Fehler (MQF) zur Varianz des Schätzers:

$\operatorname {MQF} (T,\vartheta ):=\operatorname {Var} _{\vartheta }(T)+\left(\operatorname {Bias} _{\vartheta }(T)\right)^{2}=\operatorname {Var} _{\vartheta }(T)$ .

Optimalität

Erwartungstreue an sich ist bereits ein Qualitätskriterium, da erwartungstreue Schätzer immer eine Verzerrung von Null haben und somit im Mittel den zu schätzenden Wert liefern. Sie haben also keinen systematischen Fehler. In der Menge der erwartungstreuen Schätzer reduziert sich das zentrale Qualitätskriterium für Schätzer, der mittere quadratische Fehler, zu Varianz der Schätzer. Demnach vergleichen die beiden gängigen Optimalitätskriterien die Varianzen von Punktschätzern.

Lokal minimale Schätzer vergleichen die Varianzen von Punktschätzern für ein vorgegebenes $\vartheta _{0}\in \Theta$ . Ein Schätzer heißt dann ein lokal minimaler Schätzer in $\vartheta _{0}$ , wenn

$\operatorname {Var} _{\vartheta _{0}}(S)\leq \operatorname {Var} _{\vartheta _{0}}(T)$

für alle weiteren erwartungstreuen Schätzer gilt.

Gleichmäßig bester erwartungstreue Schätzer verschärfen diese Forderung dahingehend, dass ein Schätzer für alle $\vartheta \in \Theta$ eine kleinere Varianz als jeder weitere erwartungstreue Schätzer haben soll. Es gilt dann also

$\operatorname {Var} _{\vartheta }(S)\leq \operatorname {Var} _{\vartheta }(T){\text{ für alle }}\vartheta \in \Theta$

und alle erwartungstreuen Schätzer .

Erwartungstreue vs. mittlerer quadratischer Fehler

Erwartungstreue Schätzer sind auf zwei Arten als „gut“ anzusehen:

Einerseits ist ihre Verzerrung immer gleich null; sie haben demnach die wünschenswerte Eigenschaft, keinen systematischen Fehler aufzuweisen.
Andererseits ist aufgrund der Zerlegung des mittleren quadratischen Fehlers in Verzerrung und Varianz der mittlere quadratische Fehler eines erwartungstreuen Schätzers immer automatisch klein, da die Verzerrung wegfällt.

Allerdings können nicht immer beide Ziele (Erwartungstreue und minimaler quadratischer Fehler) gleichzeitig erfüllt werden. So ist im Binomialmodell $X=\{0,\dots ,n\},{\mathcal {A}}={\mathcal {P}}(X),P_{\vartheta }=\operatorname {Bin} _{n,\vartheta }$ mit $\vartheta \in [0,1]$ ein gleichmäßig bester erwartungstreuer Schätzer gegeben durch

$T_{1}(x)={\frac {x}{n}}$ .

Der Schätzer

$T_{2}={\frac {x+1}{n+2}}$

ist nicht erwartungstreu und folglich verzerrt, besitzt aber für Werte von $\vartheta$ nahe an $0{,}5$ einen geringeren mittleren quadratischen Fehler.

Es können also nicht immer Verzerrung und mittlerer quadratischer Fehler gleichzeitig minimiert werden.

Schätzer mit Verzerrung

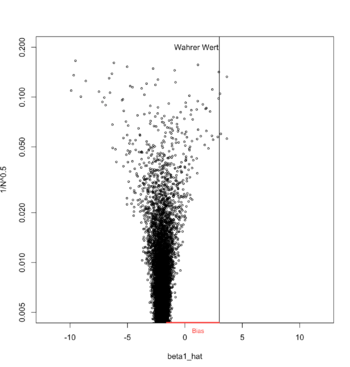
Diese Graphik zeigt eine Verletzung der Unverzerrtheits- und Konsistenzeigenschaft. Es wird im Mittel nicht der wahre Wert 3 geschätzt, sondern -2. Somit ergibt sich eine Verzerrung von 5: $\mathrm {Bias} ({\hat {\beta }}_{1})=\operatorname {E} ({\hat {\beta }}_{1})-\beta _{1}=3-(-2)=5$

Es ergibt sich aus der Definition, dass „gute“ Schätzer zumindest näherungsweise erwartungstreu sein, sich also dadurch auszeichnen sollen, dass sie im Mittel nah am zu schätzenden Wert liegen. Üblicherweise ist Erwartungstreue jedoch nicht das einzige wichtige Kriterium für die Qualität eines Schätzers; so sollte er beispielsweise auch eine kleine Varianz haben, also möglichst gering um den zu schätzenden Wert schwanken. Zusammengefasst ergibt sich das klassische Kriterium einer minimalen mittleren quadratischen Abweichung für optimale Schätzer.

Die Verzerrung ${\mathrm {Bias}}_{{\vartheta }}(T)$ eines Schätzers ist definiert als Differenz zwischen seinem Erwartungswert und der zu schätzenden Größe:

$\mathrm {Bias} _{\vartheta }(T):=\operatorname {E} _{\vartheta }(T)-\gamma (\vartheta )=\operatorname {E} _{\vartheta }(T-\gamma (\vartheta )).$

Sein mittlerer quadratischer Fehler ${\mathrm {MSE}}_{{\vartheta }}(T)$ ist

$\mathrm {MSE} _{\vartheta }(T):=\operatorname {E} _{\vartheta }{\bigl (}(T-\gamma (\vartheta ))^{2}{\bigr )}.$

Der mittlere quadratische Fehler ist gleich der Summe des Quadrats der Verzerrung und der Varianz des Schätzers:

${\mathrm {MSE}}_{{\vartheta }}(T)={\bigl (}{\mathrm {Bias}}_{{\vartheta }}(T){\bigr )}^{2}+\operatorname {Var}_{{\vartheta }}(T).$

In der Praxis kann eine Verzerrung zwei Ursachen haben:

einen systematischen Fehler, beispielsweise ein nicht-zufälliger Messfehler in der Apparatur, oder
einen zufälligen Fehler, dessen Erwartungswert ungleich 0 ist.

Zufällige Fehler können tolerabel sein, wenn sie dazu beitragen, dass der Schätzer eine kleinere minimale quadratische Abweichung als ein unverzerrter besitzt.

Asymptotische Erwartungstreue

→ Hauptartikel: Asymptotische Erwartungstreue

In der Regel ist es nicht von Bedeutung, dass ein Schätzer erwartungstreu ist. Die meisten Resultate der mathematischen Statistik gelten erst asymptotisch, also wenn der Stichprobenumfang ins Unendliche wächst. Daher ist es in der Regel ausreichend, wenn Erwartungstreue im Grenzwert gilt, d. h. für eine Folge von Schätzern T_n die Konvergenzaussage $\textstyle \lim _{n\rightarrow \infty }\operatorname {E} _{\vartheta }(T_{n})=\gamma (\vartheta )$ gilt.

Weiteres Beispiel: Stichprobenvarianz im Normalverteilungsmodell

Ein typisches Beispiel sind Schätzer für die Parameter von Normalverteilungen. Man betrachtet in diesem Fall die parametrische Familie

$P_{{\vartheta }},\;\vartheta \in \Theta$ mit $\vartheta =(\mu ,\sigma ^{2})$ und $\Theta ={\mathbb R}\times {\mathbb R}^{{+}}$ ,

wobei $P_{\vartheta }$ die Normalverteilung mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ ist. Üblicherweise sind Beobachtungen $X_1, \dotsc, X_n$ gegeben, die stochastisch unabhängig sind und jeweils die Verteilung $P_{\vartheta }$ besitzen.

Wie bereits gesehen, ist das Stichprobenmittel $\overline {X}_{n}$ ein erwartungstreuer Schätzer von $\gamma _{1}(\vartheta )=\mu$ .

Für die Varianz $\gamma _{2}(\vartheta )=\sigma ^{2}$ erhält man als Maximum-Likelihood-Schätzer $\textstyle s_{n}^{2}={\frac 1n}\sum _{{i=1}}^{n}(X_{i}-\overline {X}_{n})^{2}$ . Dieser Schätzer ist allerdings nicht erwartungstreu, da sich $\textstyle \operatorname {E} (s_{n}^{2})={\frac {n-1}{n}}\sigma ^{2}$ zeigen lässt (siehe Stichprobenvarianz (Schätzfunktion)#Erwartungstreue). Die Verzerrung beträgt also $\textstyle \operatorname {E} (s_{n}^{2})-\sigma ^{2}=-{\frac {1}{n}}\sigma ^{2}$ . Da diese asymptotisch, also für $n\rightarrow \infty$ , verschwindet, ist der Schätzer allerdings asymptotisch erwartungstreu.

Darüber hinaus kann man in diesem Fall den Erwartungswert der Verzerrung genau angeben und folglich die Verzerrung korrigieren, indem man mit $\tfrac{n}{n-1}$ multipliziert (sog. Bessel-Korrektur), und erhält so einen Schätzer für die Varianz, der auch für kleine Stichproben erwartungstreu ist.

Im Allgemeinen ist es jedoch nicht möglich, die erwartete Verzerrung exakt zu bestimmen und somit vollständig zu korrigieren. Es gibt aber Verfahren, um die Verzerrung eines asymptotisch erwartungstreuen Schätzers für endliche Stichproben zumindest zu verringern, zum Beispiel das sogenannte Jackknife.

Aufbauende Begriffe

Ein erwartungstreuer Schätzer heißt ein regulärer erwartungstreuer Schätzer, wenn

${\frac {\partial }{\partial \vartheta }}\int T(x)\cdot f_{{\vartheta }}(x)\,dx=\int T(x)\cdot {\frac {\partial }{\partial \vartheta }}f_{{\vartheta }}(x)\,dx$

gilt. $f_{\vartheta }$ bezeichnet hier die Dichtefunktion zum Parameter $\vartheta$ . Differentiation und Integration sollen also vertauschbar sein. Reguläre erwartungstreue Schätzer spielen eine wichtige Rolle in der Cramér-Rao-Ungleichung.

Verallgemeinerungen

Eine Verallgemeinerung der Erwartungstreue ist die L-Unverfälschtheit, sie verallgemeinert die Erwartungstreue mittels allgemeinerer Verlustfunktionen. Bei Verwendung des Gauß-Verlustes erhält man die Erwartungstreue als Spezialfall, bei Verwendung des Laplace-Verlustes die Median-Unverfälschtheit.

Basierend auf einem Artikel in:

Wikipedia.de