
Verlustfunktion (Statistik)
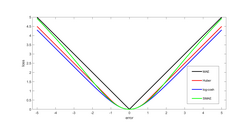
Eine Verlustfunktion (engl. loss function) ist eine spezielle Funktion in der mathematischen Statistik und Teil eines statistischen Entscheidungsproblemes. Sie ordnet jeder Entscheidung in Form einer Punktschätzung, einer Bereichsschätzung oder eines Tests den Schaden zu, der durch eine vom wahren Parameter abweichende Entscheidung entsteht. Gemeinsam mit der Entscheidungsfunktion wird die Verlustfunktion zur Risikofunktion kombiniert, die den potentiellen Schaden bei Verwendung einer Entscheidungsfunktion angibt.
Definition
Gegeben sei ein statistisches Modell
und ein
Entscheidungsraum
. Dann heißt eine Funktion
eine Verlustfunktion, wenn für jedes fixierte
die Funktion
-messbar ist. Das L steht dabei für loss, englisch für Verlust.
Die Verlustfunktion gibt den Verlust bei Vorliegen des Parameters
an, wenn man sich für
entscheidet.
Klassische Verlustfunktionen
Gegeben sei die Parameterfunktion
von der Parametermenge
in die Entscheidungsmenge
,
also
und eine
Norm
auf der Entscheidungsmenge. Meist ist
.
Eine typische Verlustfunktion ist dann
für ein .
Im Rahmen der Probabilistischen Klassifikation können Scoring rules als Verlustfunktion eingesetzt werden.
Laplace-Verlust
Ist , also
,
so spricht man vom Laplace-Verlust.
Bei Wahl des Laplace-Verlusts die L-Unverfälschtheit zur Median-Unverfälschtheit und die Risikofunktion zum Mittleren betraglichen Fehler.
Gauß-Verlust
Ist , also
,
so spricht man vom Gauß-Verlust.
Wählt man in der Schätztheorie den Gauß-Verlust, so vereinfacht sich die L-Unverfälschtheit zur Erwartungstreue und die Risikofunktion zum mittleren quadratischen Fehler.
0-1-Verlust
Eine weitere wichtige Verlustfunktion ist der sogenannte 0-1-Verlust. Er ist definiert als
für ein .
Er bestraft alle Entscheidungen, die nahe genug an der „richtigen“ Entscheidung liegen, überhaupt nicht und alle, die einen gewissen Abstand zu ihr überschreiten, gleich stark. Im Rahmen von den
mengenwertigen Bereichsschätzern wird der 0-1-Verlust dann auch definiert als
,
da die Entscheidungen dann Mengen und keine einzelnen Werte mehr sind.
Neyman-Pearson-Verlustfunktion
Für statistische Tests verwendet man eine Abwandlung des 0-1-Verlustes, die sogenannten Neyman-Pearson-Verlustfunktion. Ist
eine Zerlegung des Parameterraumes in Hypothese
und Alternative
sowie
die Entscheidung für die Hypothese und
die Entscheidung für die Alternative, so wird die Verlustfunktion definiert durch
.
Dabei ist .
entspricht dann dem Verlust bei einem
Fehler 1. Art,
bei einem Fehler 2. Art.
Literatur
- Ludger Rüschendorf: Mathematische Statistik. Springer Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-41996-6,
doi:
 10.1007/978-3-642-41997-3.
10.1007/978-3-642-41997-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.11. 2025