Normalverteilung
| Normalverteilung | |
Dichtefunktion 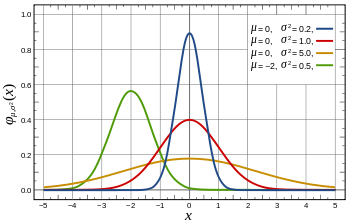 Dichtefunktionen der Normalverteilung Dichtefunktionen der Normalverteilung | |
Verteilungsfunktion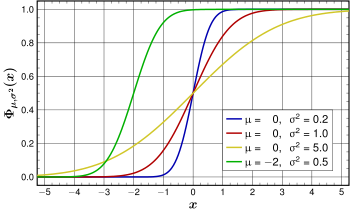 Verteilungsfunktionen der
Normalverteilungen: Verteilungsfunktionen der
Normalverteilungen: | |
| Parameter | |
|---|---|
| Träger | |
| Dichtefunktion | |
| Verteilungsfunktion | – mit Fehlerfunktion |
| Erwartungswert | |
| Median | |
| Modus | |
| Varianz | |
| Schiefe | |
| Wölbung | |
| Entropie | |
| Momenterzeugende Funktion | |
| Charakteristische Funktion | |
| Fisher-Information | |
Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist in der Stochastik ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichtefunktion wird auch Gauß-Funktion, Gaußsche Normalverteilung, Gaußsche Verteilungskurve, Gauß-Kurve, Gaußsche Glockenkurve, Gaußsche Glockenfunktion, Gauß-Glocke oder schlicht Glockenkurve genannt.
Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch additive Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind. Die Familie der Normalverteilungen bildet eine Lage- und Skalenfamilie.
Die Abweichungen der Messwerte vieler natur-, wirtschafts- und ingenieurwissenschaftlicher Vorgänge vom Erwartungswert lassen sich durch die Normalverteilung (bei biologischen Prozessen oft logarithmische Normalverteilung) entweder exakt oder wenigstens in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).
Zufallsvariablen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie:
- zufällige Streuung von Messwerten,
- zufällige Abweichungen vom Sollmaß bei der Fertigung von Werkstücken,
- Beschreibung der brownschen Molekularbewegung.
In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen.
In der Messtechnik wird häufig eine Normalverteilung angesetzt, die die Streuung der Messfehler beschreibt. Hierbei ist von Bedeutung, wie viele Messpunkte innerhalb einer gewissen Streubreite liegen.
Die Standardabweichung
beschreibt die Breite der Normalverteilung. Die Halbwertsbreite
einer Normalverteilung ist das ungefähr
-Fache
(genau
)
der Standardabweichung. Es gilt näherungsweise:
- Im Intervall der Abweichung
vom Erwartungswert sind 68,27 % aller Messwerte zu finden,
- Im Intervall der Abweichung
vom Erwartungswert sind 95,45 % aller Messwerte zu finden,
- Im Intervall der Abweichung
vom Erwartungswert sind 99,73 % aller Messwerte zu finden.
Und ebenso lassen sich umgekehrt für gegebene Wahrscheinlichkeiten die maximalen Abweichungen vom Erwartungswert finden:
- 50 % aller Messwerte haben eine Abweichung von höchstens
vom Erwartungswert,
- 90 % aller Messwerte haben eine Abweichung von höchstens
vom Erwartungswert,
- 95 % aller Messwerte haben eine Abweichung von höchstens
vom Erwartungswert,
- 99 % aller Messwerte haben eine Abweichung von höchstens
vom Erwartungswert.
Somit kann neben dem Erwartungswert, der als Schwerpunkt der Verteilung interpretiert werden kann, auch der Standardabweichung eine einfache Bedeutung im Hinblick auf die Größenordnungen der auftretenden Wahrscheinlichkeiten bzw. Häufigkeiten zugeordnet werden.
Geschichte

Im Jahre 1733 zeigte Abraham de Moivre in seiner Schrift The Doctrine of Chances im Zusammenhang mit seinen Arbeiten am Grenzwertsatz für Binomialverteilungen eine Abschätzung des Binomialkoeffizienten, die als Vorform der Normalverteilung gedeutet werden kann. Die für die Normierung der Normalverteilungsdichte zur Wahrscheinlichkeitsdichte notwendige Berechnung des nichtelementaren Integrals
gelang Pierre-Simon Laplace im Jahr 1782 (nach anderen Quellen Poisson). Im Jahr 1809 publizierte Gauß sein Werk Theoria motus corporum coelestium in sectionibus conicis solem ambientium (deutsch Theorie der Bewegung der in Kegelschnitten sich um die Sonne bewegenden Himmelskörper), das neben der Methode der kleinsten Quadrate und der Maximum-Likelihood-Schätzung die Normalverteilung definiert. Ebenfalls Laplace war es, der 1810 den Satz vom zentralen Grenzwert bewies, der die Grundlage der theoretischen Bedeutung der Normalverteilung darstellt und de Moivres Arbeit am Grenzwertsatz für Binomialverteilungen abschloss. Adolphe Quetelet erkannte schließlich bei Untersuchungen des Brustumfangs von mehreren tausend Soldaten im Jahr 1844 eine verblüffende Übereinstimmung mit der Normalverteilung und brachte die Normalverteilung in die angewandte Statistik. Er hat vermutlich die Bezeichnung „Normalverteilung“ geprägt.
Definition
Eine stetige
Zufallsvariable
hat eine (Gauß- oder) Normalverteilung mit Erwartungswert
und Varianz
(
),
oft geschrieben als
,
wenn
die folgende Wahrscheinlichkeitsdichte
hat:[1]
.
Der Graph dieser Dichtefunktion hat eine „glockenförmige
Gestalt“ und ist symmetrisch
mit dem Parameter
als Symmetriezentrum, der auch den Erwartungswert,
den Median
und den Modus
der Verteilung darstellt. Die Varianz von
ist der Parameter
.
Weiterhin hat die Wahrscheinlichkeitsdichte Wendepunkte
bei
.
Die Wahrscheinlichkeitsdichte einer normalverteilten Zufallsvariable hat kein
definites Integral, das in geschlossener Form lösbar ist, sodass
Wahrscheinlichkeiten numerisch berechnet werden müssen. Die Wahrscheinlichkeiten
können mithilfe einer Standardnormalverteilungstabelle
berechnet werden, die eine Standardform
verwendet. Um das zu sehen, benutzt man die Tatsache, dass eine lineare Funktion einer
normalverteilten Zufallsvariablen selbst wieder normalverteilt ist. Konkret
heißt das, wenn
und
,
wobei
und
Konstanten sind mit
,
dann gilt
.
Als Folgerung daraus ergibt sich die Zufallsvariable
,
die auch standardnormalverteilte Zufallsvariable
genannt wird. Die Standardnormalverteilung ist also die Normalverteilung
mit Parametern
und
.
Die Dichtefunktion der Standardnormalverteilung ist gegeben durch
.
Ihr Verlauf ist nebenstehend graphisch dargestellt.
Die mehrdimensionale Verallgemeinerung ist im Artikel mehrdimensionale Normalverteilung zu finden.
Eigenschaften
Verteilungsfunktion
Die Verteilungsfunktion der Normalverteilung ist durch
gegeben. Wenn man durch die Substitution
statt
eine neue Integrationsvariable
einführt, ergibt sich
Dabei ist
die Verteilungsfunktion der Standardnormalverteilung
Mit der Fehlerfunktion
lässt sich
darstellen als
.
Symmetrie
Der Graph
der Wahrscheinlichkeitsdichte
ist eine Gaußsche Glockenkurve, deren Höhe und Breite von
abhängt. Sie ist achsensymmetrisch
zur Geraden mit der Gleichung
und somit eine symmetrische
Wahrscheinlichkeitsverteilung um ihren Erwartungswert. Der Graph der
Verteilungsfunktion
ist punktsymmetrisch
zum Punkt
Für
gilt insbesondere
und
für alle
.
Maximalwert und Wendepunkte der Dichtefunktion
Mit Hilfe der ersten und zweiten Ableitung lassen sich der Maximalwert und die Wendepunkte bestimmen. Die erste Ableitung ist
Das Maximum der Dichtefunktion der Normalverteilung liegt demnach bei
und beträgt dort
.
Die zweite Ableitung lautet
.
Somit liegen die Wendestellen
der Dichtefunktion bei .
Die Dichtefunktion hat an den Wendestellen den Wert
.
Normierung
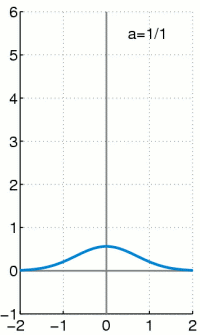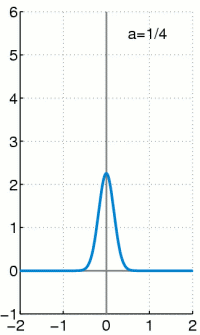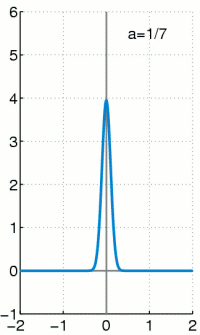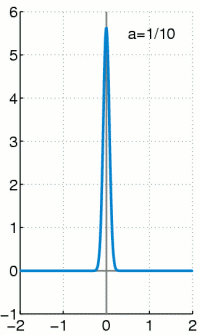
Für
Wichtig ist, dass die gesamte Fläche
unter der Kurve gleich ,
also gleich der Wahrscheinlichkeit des sicheren Ereignisses,
ist. Somit folgt, dass, wenn zwei Gaußsche Glockenkurven dasselbe
,
aber unterschiedliches
haben, die Kurve mit dem größeren
breiter und niedriger ist (da ja beide zugehörigen Flächen jeweils den Wert
haben und nur die Standardabweichung größer ist). Zwei Glockenkurven mit
gleichem
aber unterschiedlichem
haben kongruente Graphen, die um die Differenz der
-Werte
parallel zur
-Achse
gegeneinander verschoben sind.
Jede Normalverteilung ist tatsächlich normiert, denn mit Hilfe der linearen
Substitution
erhalten wir
.
Für die Normiertheit des letzteren Integrals siehe Fehlerintegral.
Berechnung
Da sich
nicht auf eine elementare Stammfunktion
zurückführen lässt, wurde für die Berechnung früher meist auf Tabellen
zurückgegriffen .
Heutzutage sind in statistischen Programmiersprachen wie zum Beispiel R Funktionen
verfügbar, die auch die Transformation auf beliebige
und
beherrschen.
Erwartungswert
Der Erwartungswert
der Standardnormalverteilung ist .
Es sei
,
so gilt
da der Integrand integrierbar und punktsymmetrisch ist.
Ist nun ,
so gilt
ist standardnormalverteilt, und somit
Varianz und weitere Streumaße
Die Varianz
der -normalverteilten
Zufallsvariablen entspricht dem Parameter
.
Ein elementarer Beweis wird Poisson zugeschrieben.
Die mittlere
absolute Abweichung ist
und der Interquartilsabstand
.
Standardabweichung der Normalverteilung
Eindimensionale Normalverteilungen werden durch Angabe von Erwartungswert
und Varianz
vollständig beschrieben. Ist also
eine
-
-verteilte
Zufallsvariable – in Symbolen
–, so ist ihre Standardabweichung einfach
.
Streuintervalle
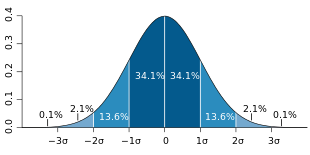
Aus der Standardnormalverteilungstabelle ist ersichtlich, dass für normalverteilte Zufallsvariablen jeweils ungefähr
- 68,3 % der Realisierungen
im Intervall
,
- 95,4 % im Intervall
und
- 99,7 % im Intervall
liegen. Da in der Praxis viele Zufallsvariablen annähernd normalverteilt
sind, werden diese Werte aus der Normalverteilung oft als Faustformel benutzt.
So wird beispielsweise
oft als die halbe Breite des Intervalls angenommen, das die mittleren zwei
Drittel der Werte in einer Stichprobe umfasst, siehe Quantil.
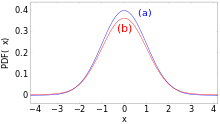
Diese Praxis ist aber nicht empfehlenswert, denn sie kann zu sehr großen
Fehlern führen. Zum Beispiel ist die Verteilung
optisch kaum von der Normalverteilung zu unterscheiden (siehe Bild), aber bei
ihr liegen im Intervall
92,5 % der Werte, wobei
die Standardabweichung von
bezeichnet. Solche kontaminierten
Normalverteilungen sind in der Praxis sehr häufig; das genannte Beispiel
beschreibt die Situation, wenn zehn Präzisionsmaschinen etwas herstellen, aber
eine davon schlecht justiert ist und mit zehnmal so hohen Abweichungen wie die
anderen neun produziert.
Werte außerhalb der zwei- bis dreifachen Standardabweichung werden oft als Ausreißer behandelt. Ausreißer können ein Hinweis auf grobe Fehler der Datenerfassung sein. Es kann den Daten aber auch eine stark schiefe Verteilung zugrunde liegen. Andererseits liegt bei einer Normalverteilung im Durchschnitt ca. jeder 20. Messwert außerhalb der zweifachen Standardabweichung und ca. jeder 500. Messwert außerhalb der dreifachen Standardabweichung.
Da der Anteil der Werte außerhalb der sechsfachen Standardabweichung mit ca.
2 ppb
verschwindend klein wird, gilt ein solches Intervall als gutes Maß für eine
nahezu vollständige Abdeckung aller Werte. Das wird im Qualitätsmanagement durch
die Methode Six Sigma genutzt, indem die
Prozessanforderungen Toleranzgrenzen von mindestens
vorschreiben. Allerdings geht man dort von einer langfristigen
Erwartungswertverschiebung um 1,5 Standardabweichungen aus, sodass der zulässige
Fehleranteil auf 3,4 ppm
steigt. Dieser Fehleranteil entspricht einer viereinhalbfachen
Standardabweichung (
).
Ein weiteres Problem der
-Methode
ist, dass die
-Punkte
praktisch nicht bestimmbar sind. Bei unbekannter Verteilung (d.h., wenn es
sich nicht ganz sicher um eine Normalverteilung handelt) grenzen zum
Beispiel die Extremwerte von 1.400.000.000 Messungen ein 75-%-Konfidenzintervall
für die
-Punkte
ein.
| Prozent innerhalb | Prozent außerhalb | ppb außerhalb | Bruchteil außerhalb | |
|---|---|---|---|---|
| 0,674490 |
50 % | 50 % | 500.000.000 | 1 / 2 |
| 0,994458 |
68 % | 32 % | 320.000.000 | 1 / 3,125 |
| 1 |
68,268 9492 % | 31,731 0508 % | 317.310.508 | 1 / 3,151 4872 |
| 1,281552 |
80 % | 20 % | 200.000.000 | 1 / 5 |
| 1,644854 |
90 % | 10 % | 100.000.000 | 1 / 10 |
| 1,959964 |
95 % | 5 % | 50.000.000 | 1 / 20 |
| 2 |
95,449 9736 % | 4,550 0264 % | 45.500.264 | 1 / 21,977 895 |
| 2,354820 |
98,146 8322 % | 1,853 1678 % | 18.531.678 | 1 / 54 |
| 2,575829 |
99 % | 1 % | 10.000.000 | 1 / 100 |
| 3 |
99,730 0204 % | 0,269 9796 % | 2.699.796 | 1 / 370,398 |
| 3,290527 |
99,9 % | 0,1 % | 1.000.000 | 1 / 1.000 |
| 3,890592 |
99,99 % | 0,01 % | 100.000 | 1 / 10.000 |
| 4 |
99,993 666 % | 0,006 334 % | 63.340 | 1 / 15.787 |
| 4,417173 |
99,999 % | 0,001 % | 10.000 | 1 / 100.000 |
| 4,891638 |
99,9999 % | 0,0001 % | 1.000 | 1 / 1.000.000 |
| 5 |
99,999 942 6697 % | 0,000 057 3303 % | 573,3303 | 1 / 1.744.278 |
| 5,326724 |
99,999 99 % | 0,000 01 % | 100 | 1 / 10.000.000 |
| 5,730729 |
99,999 999 % | 0,000 001 % | 10 | 1 / 100.000.000 |
| 6 |
99,999 999 8027 % | 0,000 000 1973 % | 1,973 | 1 / 506.797.346 |
| 6,109410 |
99,999 9999 % | 0,000 0001 % | 1 | 1 / 1.000.000.000 |
| 6,466951 |
99,999 999 99 % | 0,000 000 01 % | 0,1 | 1 / 10.000.000.000 |
| 6,806502 |
99,999 999 999 % | 0,000 000 001 % | 0,01 | 1 / 100.000.000.000 |
| 7 |
99,999 999 999 7440 % | 0,000 000 000 256 % | 0,002 56 | 1 / 390.682.215.445 |
Die Wahrscheinlichkeiten
für bestimmte Streuintervalle
können berechnet werden als
,
wobei
die Verteilungsfunktion
der Standardnormalverteilung ist.
Umgekehrt können für gegebenes
durch
die Grenzen des zugehörigen Streuintervalls
mit Wahrscheinlichkeit
berechnet werden.
Ein Beispiel (mit Schwankungsbreite)
Die Körpergröße des Menschen ist näherungsweise normalverteilt. Bei einer Stichprobe von 1.284 Mädchen und 1.063 Jungen zwischen 14 und 18 Jahren wurde bei den Mädchen eine durchschnittliche Körpergröße von 166,3 cm (Standardabweichung 6,39 cm) und bei den Jungen eine durchschnittliche Körpergröße von 176,8 cm (Standardabweichung 7,46 cm) gemessen.
Demnach lässt obige Schwankungsbreite erwarten, dass 68,3 % der Mädchen eine Körpergröße im Bereich 166,3 cm ± 6,39 cm und 95,4 % im Bereich 166,3 cm ± 12,8 cm haben,
- 16 % [≈ (100 % − 68,3 %)/2] der Mädchen kleiner als 160 cm (und 16 % entsprechend größer als 173 cm) sind und
- 2,5 % [≈ (100 % − 95,4 %)/2] der Mädchen kleiner als 154 cm (und 2,5 % entsprechend größer als 179 cm) sind.
Für die Jungen lässt sich erwarten, dass 68 % eine Körpergröße im Bereich 176,8 cm ± 7,46 cm und 95 % im Bereich 176,8 cm ± 14,92 cm haben,
- 16 % der Jungen kleiner als 169 cm (und 16 % größer als 184 cm) und
- 2,5 % der Jungen kleiner als 162 cm (und 2,5 % größer als 192 cm) sind.
Variationskoeffizient
Aus Erwartungswert
und Standardabweichung
der
-Verteilung
erhält man unmittelbar den Variationskoeffizienten
Schiefe
Die Schiefe
besitzt unabhängig von den Parametern
und
immer den Wert
.
Wölbung
Die Wölbung
ist ebenfalls von
und
unabhängig und ist gleich
.
Um die Wölbungen anderer Verteilungen besser einschätzen zu können, werden sie
oft mit der Wölbung der Normalverteilung verglichen. Dabei wird die Wölbung der
Normalverteilung auf
normiert (Subtraktion von 3); diese Größe wird als Exzess
bezeichnet.
Kumulanten
Die kumulantenerzeugende Funktion ist
Damit ist die erste Kumulante
,
die zweite ist
und alle weiteren Kumulanten verschwinden.
Charakteristische Funktion
Die charakteristische
Funktion für eine standardnormalverteilte Zufallsvariable
ist
.
Für eine Zufallsvariable
erhält man daraus mit
:
.
Momenterzeugende Funktion
Die momenterzeugende Funktion der Normalverteilung lautet
.
Momente
Die Zufallsvariable
sei
-verteilt.
Dann sind ihre ersten Momente wie folgt:
| Ordnung | Moment | zentrales Moment |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Alle zentralen Momente
lassen sich durch die Standardabweichung
darstellen:
dabei wurde die Doppelfakultät verwendet:
Auch für
kann eine Formel für nicht-zentrale Momente angegeben werden. Dafür
transformiert man
und wendet den binomischen Lehrsatz an.
Invarianz gegenüber Faltung
Die Normalverteilung ist invariant gegenüber der Faltung,
d.h., die Summe unabhängiger normalverteilter Zufallsvariablen ist wieder
normalverteilt (siehe dazu auch unter stabile
Verteilungen bzw. unter unendliche
teilbare Verteilungen). Somit bildet die Normalverteilung eine
Faltungshalbgruppe
in ihren beiden Parametern. Eine veranschaulichende Formulierung dieses
Sachverhaltes lautet: Die Faltung einer Gaußkurve der Halbwertsbreite
mit einer Gaußkurve der Halbwertsbreite
ergibt wieder eine Gaußkurve mit der Halbwertsbreite
.
Sind also
zwei unabhängige Zufallsvariablen mit
so ist deren Summe ebenfalls normalverteilt:
.
Das kann beispielsweise mit Hilfe von charakteristischen Funktionen gezeigt werden, indem man verwendet, dass die charakteristische Funktion der Summe das Produkt der charakteristischen Funktionen der Summanden ist (vgl. Faltungssatz der Fouriertransformation).
Gegeben seien allgemeiner
unabhängige und normalverteilte Zufallsvariablen
.
Dann ist jede Linearkombination
wieder normalverteilt
insbesondere ist die Summe der Zufallsvariablen wieder normalverteilt
und das arithmetische Mittel ebenfalls
Nach dem Satz von Cramér gilt sogar die Umkehrung: Ist eine normalverteilte Zufallsvariable die Summe von unabhängigen Zufallsvariablen, dann sind die Summanden ebenfalls normalverteilt.
Die Dichtefunktion der Normalverteilung ist ein Fixpunkt der Fourier-Transformation, d.h., die Fourier-Transformierte einer Gaußkurve ist wieder eine Gaußkurve. Das Produkt der Standardabweichungen dieser korrespondierenden Gaußkurven ist konstant; es gilt die Heisenbergsche Unschärferelation.
Entropie
Die Normalverteilung hat die Entropie:
.
Da sie für gegebenen Erwartungswert und gegebene Varianz die größte Entropie unter allen Verteilungen hat, wird sie in der Maximum-Entropie-Methode oft als A-priori-Wahrscheinlichkeit verwendet.
Beziehungen zu anderen Verteilungsfunktionen
Transformation zur Standardnormalverteilung
Eine Normalverteilung mit beliebigen
und
und der Verteilungsfunktion
hat, wie oben erwähnt, die nachfolgende Beziehung zur >
-Verteilung:
.
Darin ist
die Verteilungsfunktion der Standardnormalverteilung.
Wenn ,
dann führt die Standardisierung
zu einer standardnormalverteilten Zufallsvariablen ,
denn
.
Geometrisch betrachtet entspricht die durchgeführte Substitution einer
flächentreuen Transformation der Glockenkurve von
zur Glockenkurve von
.
Approximation der Binomialverteilung durch die Normalverteilung
Die Normalverteilung kann zur Approximation der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und in der Grundgesamtheit der Anteil der gesuchten Eigenschaft weder zu groß noch zu klein ist (Satz von Moivre-Laplace, zentraler Grenzwertsatz.
Ist ein Bernoulli-Versuch mit
voneinander unabhängigen Stufen (bzw. Zufallsexperimenten)
mit einer Erfolgswahrscheinlichkeit
gegeben, so lässt sich die Wahrscheinlichkeit für
Erfolge allgemein durch
berechnen (Binomialverteilung).
Diese Binomialverteilung kann durch eine Normalverteilung approximiert
werden, wenn
hinreichend groß und
weder zu groß noch zu klein ist. Als Faustregel dafür gilt
.
Für den Erwartungswert
und die Standardabweichung
gilt dann:
und
.
Damit gilt für die Standardabweichung .
Falls diese Bedingung nicht erfüllt sein sollte, ist die Ungenauigkeit der
Näherung immer noch vertretbar, wenn gilt:
und zugleich
.
Folgende Näherung ist dann brauchbar:
Bei der Normalverteilung wird die untere Grenze um 0,5 verkleinert und die
obere Grenze um 0,5 vergrößert, um eine bessere Approximation gewährleisten zu
können. Dies nennt man auch „Stetigkeitskorrektur“. Nur wenn
einen sehr hohen Wert besitzt, kann auf sie verzichtet werden.
Da die Binomialverteilung diskret ist, muss auf einige Punkte geachtet werden:
- Der Unterschied zwischen
oder
(sowie zwischen größer und größer gleich) muss beachtet werden (was ja bei der Normalverteilung nicht der Fall ist). Deshalb muss bei
die nächstkleinere natürliche Zahl gewählt werden, d.h.
-
bzw.
,
- damit mit der Normalverteilung weitergerechnet werden kann.
- Zum Beispiel:
- Außerdem ist
-
(unbedingt mit Stetigkeitskorrektur)
- und lässt sich somit durch die oben angegebene Formel berechnen.
Der große Vorteil der Approximation liegt darin, dass sehr viele Stufen einer Binomialverteilung sehr schnell und einfach bestimmt werden können.
Beziehung zur Cauchy-Verteilung
Der Quotient von zwei stochastisch
unabhängigen -standardnormalverteilten
Zufallsvariablen ist Cauchy-verteilt.
Beziehung zur Chi-Quadrat-Verteilung
Das Quadrat
einer normalverteilten Zufallsvariablen hat eine Chi-Quadrat-Verteilung
mit einem Freiheitsgrad.
Also: Wenn ,
dann
.
Weiterhin gilt: Wenn
gemeinsam stochastisch
unabhängige Chi-Quadrat-verteilte Zufallsvariablen sind, dann gilt
.
Daraus folgt mit unabhängig und standardnormalverteilten Zufallsvariablen
:
Weitere Beziehungen sind:
- Die Summe
mit
und
unabhängigen normalverteilten Zufallsvariablen
genügt einer Chi-Quadrat-Verteilung
mit
Freiheitsgraden.
- Mit steigender Anzahl an Freiheitsgraden (df ≫ 100) nähert sich die Chi-Quadrat-Verteilung der Normalverteilung an.
- Die Chi-Quadrat-Verteilung wird zur Konfidenzschätzung für die Varianz einer normalverteilten Grundgesamtheit verwendet.
Beziehung zur Rayleigh-Verteilung
Der Betrag
zweier unabhängiger normalverteilter Zufallsvariablen
,
jeweils mit Mittelwert
und gleichen Varianzen
,
ist Rayleigh-verteilt
mit Parameter
.
Beziehung zur logarithmischen Normalverteilung
Ist die Zufallsvariable
normalverteilt mit
,
dann ist die Zufallsvariable
logarithmisch-normalverteilt,
also
.
Die Entstehung einer logarithmischen Normalverteilung ist auf multiplikatives, die einer Normalverteilung auf additives Zusammenwirken vieler Zufallsvariablen zurückführen.
Beziehung zur F-Verteilung
Wenn die stochastisch unabhängigen und identisch-normalverteilten
Zufallsvariablen
und
die Parameter
besitzen, dann unterliegt die Zufallsvariable
einer F-Verteilung
mit
Freiheitsgraden. Dabei sind
.
Beziehung zur studentschen t-Verteilung
Wenn die unabhängigen Zufallsvariablen
identisch normalverteilt sind mit den Parametern
und
,
dann unterliegt die stetige Zufallsvariable
mit dem Stichprobenmittel
und der Stichprobenvarianz
einer studentschen
t-Verteilung mit
Freiheitsgraden.
Für eine zunehmende Anzahl an Freiheitsgraden nähert sich die studentsche
t-Verteilung der Normalverteilung immer näher an. Als Faustregel gilt, dass man
ab ca.
die studentsche t-Verteilung bei Bedarf durch die Normalverteilung approximieren
kann.
Die studentsche t-Verteilung wird zur Konfidenzschätzung für den Erwartungswert einer normalverteilten Zufallsvariable bei unbekannter Varianz verwendet.
Rechnen mit der Standardnormalverteilung
Bei Aufgabenstellungen, bei denen die Wahrscheinlichkeit für -
-normalverteilte
Zufallsvariablen durch die Standardnormalverteilung ermittelt werden soll, ist
es nicht nötig, die oben angegebene Transformation jedes Mal durchzurechnen.
Stattdessen wird einfach die Transformation
verwendet, um eine -verteilte
Zufallsvariable
zu erzeugen.
Die Wahrscheinlichkeit für das Ereignis, dass z.B.
im Intervall
liegt, ist durch folgende Umrechnung gleich einer Wahrscheinlichkeit der
Standardnormalverteilung:
.
Grundlegende Fragestellungen
Allgemein gibt die Verteilungsfunktion die Fläche unter
der Glockenkurve bis zum Wert
an, d.h., es wird das bestimmte Integral
von
bis
berechnet.
Dies entspricht in Aufgabenstellungen einer gesuchten Wahrscheinlichkeit,
bei der die Zufallsvariable
kleiner oder nicht größer als eine bestimmte Zahl
ist. Wegen der Stetigkeit
der Normalverteilung macht es keinen Unterschied, ob nun
oder
verlangt ist, weil z.B.
und somit
.
Analoges gilt für „größer“ und „nicht kleiner“.
Dadurch, dass
nur kleiner oder größer als eine Grenze sein (oder innerhalb oder außerhalb
zweier Grenzen liegen) kann, ergeben sich für Aufgaben bei
Wahrscheinlichkeitsberechnungen zu Normalverteilungen zwei grundlegende
Fragestellungen:
- Wie groß ist die Wahrscheinlichkeit, dass bei einem Zufallsexperiment die
standardnormalverteilte Zufallsvariable
höchstens den Wert
annimmt?
- In der Schulmathematik
wird für diese Aussage gelegentlich auch die Bezeichnung linker Spitz
verwendet, da die Fläche
unter der Gaußkurve von links bis zur Grenze verläuft. Für
sind auch negative Werte erlaubt. Allerdings haben viele Tabellen der Standardnormalverteilung nur positive Einträge – wegen der Symmetrie der Kurve und der Negativitätsregel
- des „linken Spitzes“ stellt dies aber keine Einschränkung dar.
- Wie groß ist die Wahrscheinlichkeit, dass bei einem Zufallsexperiment die
standardnormalverteilte Zufallsvariable
mindestens den Wert
annimmt?
-
- Hier wird gelegentlich die Bezeichnung rechter Spitz verwendet, mit
- gibt es auch hier eine Negativitätsregel.
Da jede Zufallsvariable
mit der allgemeinen Normalverteilung sich in die Zufallsvariable
mit der Standardnormalverteilung umwandeln lässt, gelten die Fragestellungen für
beide Größen gleichbedeutend.
Streubereich und Antistreubereich
Häufig ist die Wahrscheinlichkeit für einen Streubereich von
Interesse, d.h. die Wahrscheinlichkeit, dass die standardnormalverteilte
Zufallsvariable
Werte zwischen
und
annimmt:
Beim Sonderfall des symmetrischen Streubereiches (,
mit
)
gilt
Für den entsprechenden Antistreubereich ergibt sich die
Wahrscheinlichkeit, dass die standardnormalverteilte Zufallsvariable
Werte außerhalb des Bereichs zwischen
und
annimmt, zu:
Somit folgt bei einem symmetrischen Antistreubereich
Streubereiche am Beispiel der Qualitätssicherung
Besondere Bedeutung haben beide Streubereiche z.B. bei der Qualitätssicherung
von technischen oder wirtschaftlichen Produktionsprozessen.
Hier gibt es einzuhaltende Toleranzgrenzen
und
,
wobei es meist einen größten noch akzeptablen Abstand
vom Erwartungswert
(= dem optimalen Sollwert) gibt. Die Standardabweichung
kann hingegen empirisch
aus dem Produktionsprozess gewonnen werden.
Wurde
als einzuhaltendes Toleranzintervall angegeben, so liegt (je nach Fragestellung)
ein symmetrischer Streu- oder Antistreubereich vor.
Im Falle des Streubereiches gilt:
.
Der Antistreubereich ergibt sich dann aus
oder wenn kein Streubereich berechnet wurde durch
Das Ergebnis
ist also die Wahrscheinlichkeit für verkaufbare Produkte, während
die Wahrscheinlichkeit für Ausschuss bedeutet, wobei beides von den Vorgaben von
,
und
abhängig ist.
Ist bekannt, dass die maximale Abweichung
symmetrisch um den Erwartungswert liegt, so sind auch Fragestellungen möglich,
bei denen die Wahrscheinlichkeit vorgegeben und eine der anderen Größen zu
berechnen ist.
Testen auf Normalverteilung
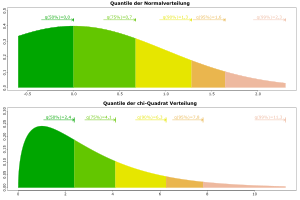
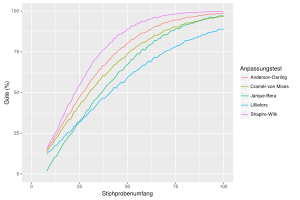
Um zu überprüfen, ob vorliegende Daten normalverteilt sind, können unter anderen folgende Methoden und Tests angewandt werden:
- Chi-Quadrat-Test
- Kolmogorow-Smirnow-Test
- Anderson-Darling-Test (Modifikation des Kolmogorow-Smirnow-Tests)
- Lilliefors-Test (Modifikation des Kolmogorow-Smirnow-Tests)
- Cramér-von-Mises-Test
- Shapiro-Wilk-Test
- Jarque-Bera-Test
- Q-Q-Plot (deskriptive Überprüfung)
- Maximum-Likelihood-Methode (deskriptive Überprüfung)
Die Tests haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. So erkennt der Kolmogorov-Smirnov-Test Abweichungen in der Mitte der Verteilung eher als Abweichungen an den Rändern, während der Jarque-Bera-Test ziemlich sensibel auf stark abweichende Einzelwerte an den Rändern („schwere Ränder“) reagiert.
Beim Lilliefors-Test muss im Gegensatz zum Kolmogorov-Smirnov-Test nicht
standardisiert werden, d.h.,
und
der angenommenen Normalverteilung dürfen unbekannt sein.
Mit Hilfe von Quantil-Quantil-Diagrammen
bzw. Normal-Quantil-Diagrammen ist eine einfache grafische Überprüfung auf
Normalverteilung möglich.
Mit der Maximum-Likelihood-Methode können die
Parameter
und
der Normalverteilung geschätzt und die empirischen Daten mit der angepassten
Normalverteilung grafisch verglichen werden.
Parameterschätzung, Konfidenzintervalle und Tests
Viele der statistischen Fragestellungen, in denen die Normalverteilung
vorkommt, sind gut untersucht. Wichtigster Fall ist das sogenannte
Normalverteilungsmodell, in dem man von der Durchführung von
unabhängigen und normalverteilten Versuchen ausgeht. Dabei treten drei Fälle
auf:
- der Erwartungswert ist unbekannt und die Varianz bekannt
- die Varianz ist unbekannt und der Erwartungswert ist bekannt
- Erwartungswert und Varianz sind unbekannt.
Je nachdem, welcher dieser Fälle auftritt, ergeben sich verschiedene Schätzfunktionen, Konfidenzbereiche oder Tests.
Dabei kommt den folgenden Schätzfunktionen eine besondere Bedeutung zu:
-
- ist ein erwartungstreuer Schätzer für den unbekannten Erwartungswert sowohl für den Fall einer bekannten als auch einer unbekannten Varianz. Er ist sogar der beste erwartungstreue Schätzer, d.h. der Schätzer mit der kleinsten Varianz. Sowohl die Maximum-Likelihood-Methode als auch die Momentenmethode liefern das Stichprobenmittel als Schätzfunktion.
- Die unkorrigierte Stichprobenvarianz
-
.
- ist ein erwartungstreuer Schätzer für die unbekannte Varianz bei gegebenem
Erwartungswert
. Auch sie kann sowohl aus der Maximum-Likelihood-Methode als auch aus der Momentenmethode gewonnen werden.
-
.
- ist ein erwartungstreuer Schätzer für die unbekannte Varianz bei unbekanntem Erwartungswert.
Erzeugung normalverteilter Zufallszahlen
Alle folgenden Verfahren erzeugen standardnormalverteilte Zufallszahlen.
Durch lineare Transformation lassen sich hieraus beliebige normalverteilte
Zufallszahlen erzeugen: Ist die Zufallsvariable -verteilt,
so ist
schließlich
-verteilt.
Box-Muller-Methode
Nach der Box-Muller-Methode
lassen sich zwei unabhängige, standardnormalverteilte Zufallsvariablen
und
aus zwei unabhängigen, gleichverteilten
Zufallsvariablen
,
sogenannten Standardzufallszahlen,
simulieren:
und
Polar-Methode
Die Polar-Methode von George Marsaglia ist auf einem Computer noch schneller, da sie keine Auswertungen von trigonometrischen Funktionen benötigt:
- Erzeuge zwei voneinander unabhängige, im Intervall
gleichverteilte Zufallszahlen
und
- Berechne
. Falls
oder
, gehe zurück zu Schritt 1.
- Berechne
.
für
liefert zwei voneinander unabhängige, standardnormalverteilte Zufallszahlen
und
.
Zwölferregel
Der zentrale Grenzwertsatz besagt, dass sich unter bestimmten Voraussetzungen die Verteilung der Summe unabhängig und identisch verteilter Zufallszahlen einer Normalverteilung nähert.
Ein Spezialfall ist die Zwölferregel, die sich auf die Summe von zwölf Zufallszahlen aus einer Gleichverteilung auf dem Intervall [0,1] beschränkt und bereits zu passablen Verteilungen führt.
Allerdings ist die geforderte Unabhängigkeit der zwölf Zufallsvariablen
bei den immer noch häufig verwendeten Linearen
Kongruenzgeneratoren (LKG) nicht garantiert. Im Gegenteil wird vom Spektraltest für LKG meist
nur die Unabhängigkeit von maximal vier bis sieben der
garantiert. Für numerische Simulationen ist die Zwölferregel daher sehr
bedenklich und sollte, wenn überhaupt, dann ausschließlich mit aufwändigeren,
aber besseren Pseudo-Zufallsgeneratoren wie z.B. dem Mersenne-Twister
(Standard in Python,
GNU R) oder WELL
genutzt werden. Andere, sogar leichter zu programmierende Verfahren, sind daher
i.d.R. der Zwölferregel vorzuziehen.
Verwerfungsmethode
Normalverteilungen lassen sich mit der Verwerfungsmethode (siehe dort) simulieren.
Inversionsmethode
Die Normalverteilung lässt sich auch mit der Inversionsmethode berechnen.
Da das Fehlerintegral
nicht explizit mit elementaren Funktionen integrierbar ist, kann man auf
Reihenentwicklungen der inversen Funktion für einen Startwert und anschließende
Korrektur mit dem Newtonverfahren zurückgreifen. Dazu werden
und
benötigt, die ihrerseits mit Reihenentwicklungen und Kettenbruchentwicklungen
berechnet werden können – insgesamt ein relativ hoher Aufwand. Die notwendigen
Entwicklungen sind in der Literatur zu finden.
Entwicklung des inversen Fehlerintegrals (wegen des Pols nur als Startwert für das Newtonverfahren verwendbar):
mit den Koeffizienten
Anwendungen außerhalb der Wahrscheinlichkeitsrechnung
Die Normalverteilung lässt sich auch zur Beschreibung nicht direkt stochastischer Sachverhalte verwenden, etwa in der Physik für das Amplitudenprofil der Gauß-Strahlen und andere Verteilungsprofile.
Zudem findet sie Verwendung in der Gabor-Transformation.
Siehe auch
Literatur
- Stephen M. Stigler: The history of statistics: the measurement of uncertainty before 1900. Belknap Series. Harvard University Press, 1986. ISBN 9780674403413.
Fußnoten
- ↑
Bei
 handelt es sich um die Exponentialfunktion
mit der Basis
handelt es sich um die Exponentialfunktion
mit der Basis 


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.11. 2024