Gauß-Strahl

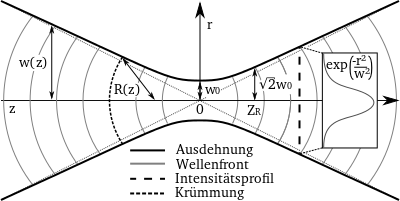
Der Gauß-Strahl (auch gaußsches Bündel) ist ein Konzept der paraxialen Optik zur Beschreibung der Lichtausbreitung, in dem sich Methoden der Strahlen- und der Wellenoptik verbinden. Im Querschnitt zeigt der Gauß-Strahl ein Profil gemäß einer Gauß-Kurve mit einer längs der Ausbreitungsachse variierenden Breite. Der Strahl verjüngt sich näherungsweise linear bis zum Erreichen der schmalsten Stelle, die als Fokus oder Taille bezeichnet wird, und wächst danach ebenso wieder an. Längs der Ausbreitungsachse zeigt die räumliche Intensität des Strahls ein Lorentzprofil, das Maximum liegt an der Stelle der Taille. Das elektromagnetische Feld des Gauß-Strahls ergibt sich aus den Maxwell-Gleichungen für konstante Frequenz ω, also aus der Helmholtz-Gleichung, nach paraxialer Näherung. Bei gegebener Ausbreitungsrichtung und Wellenlänge ist der Gauß-Strahl vollständig durch die Angabe des Orts und des Strahldurchmessers der Taille bestimmt.

Gauß-Strahlen beschreiben besonders gut die Lichtemission vieler Laser (siehe Beugungsmaßzahl), aber sie lassen sich auch in vielen anderen Situationen elektromagnetischer Strahlung einsetzen. Besonders interessant sind sie, weil sie einerseits den einfachen Rechenmethoden der Strahlenoptik gehorchen, andererseits aber auch Phasenbetrachtungen wie in der Wellenoptik erlauben.

Mathematische Beschreibung

Gauß-Strahl (schematisch) mit Abmessungen, Strahlbegrenzung, Wellenfronten und Intensitätsprofil

Zur mathematischen Beschreibung eines Gauß-Strahls werden vorzugsweise Zylinderkoordinaten verwendet. Das Koordinatensystem wird so gewählt, dass die Ausbreitungsrichtung die z-Achse ist und die Strahltaille im Koordinatenursprung bei z=0 liegt. Die komplexe Amplitude des elektrischen Feldes unter Berücksichtigung der Phase in Abhängigkeit vom Abstand zur z-Achse und der Entfernung zur Taille wird beschrieben durch die Funktion:

$E(r,z)=E_{0}\;{\frac {w_{0}}{w(z)}}\cdot \mathrm {e} ^{-\left({\frac {r}{w(z)}}\right)^{2}}\cdot \mathrm {e} ^{-ik{\frac {r^{2}}{2R(z)}}}\cdot \mathrm {e} ^{-i(kz-\zeta (z))}$

Die Phasenfläche nähert sich in großem Abstand von der Taille der einer sphärischen Welle. Mit den Näherungen der unten angegebenen Funktionen R(z) und $\zeta (z)$ für große $|z|\gg z_{R}$ wird der Phasenfaktor:

$\mathrm {e} ^{-i[k(z+{\frac {r^{2}}{2z}})\mp {\frac {\pi }{2}}]}$

Dieses Ergebnis wird nämlich ebenfalls nach Entwicklung des Quellabstands $\textstyle \rho$ im Phasenfaktor ${\mathrm {e}}^{{-ik\rho }}$ einer Kugelwelle erhalten: $\textstyle \rho ={\sqrt {r^{2}+z^{2}}}\approx z+r^{2}/(2z)$ . – Jedoch zeigt die für den Gaußstrahl charakteristische Phasenreduktion von $\pi$ nach vollständigem Durchgang durch die Taille der rotationssymmetrischen Grundmode den bedeutenden Unterschied zwischen der punktsymmetrisch strahlendenen Kugelwelle und dem gerichteten, axialsymmetrischen Strahlenbündel, siehe unten Gouy-Phase.

Die zur Feldstärke gehörende Intensität ist:

$I(r,z)={\frac {1}{2}}c_{0}\varepsilon _{0}\left|E(r,z)\right|^{2}=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}\mathrm {e} ^{-{\frac {2r^{2}}{w(z)^{2}}}}$

Dabei sind die imaginäre Einheit, $k={\tfrac {2\pi }{\lambda }}$ die Kreiswellenzahl und $E_{0}$ bzw. $I_{0}$ die Werte an der Stelle (r=0,z=0) . Die Parameterfunktionen w(z) , R(z) und $\zeta (z)$ beschreiben die Geometrie des Gauß-Strahls und werden im Folgenden erläutert.

Transversales Profil

Wie bereits erwähnt hat der Gauß-Strahl ein transversales Profil gemäß einer Gauß-Kurve. Als Strahlradius definiert man bei einem bestimmten Wert den Abstand zur -Achse, an dem die Amplitude auf 1/e (ca. 37 %), die Intensität also auf 1/e² (ca. 13,5 %), gefallen ist. Der minimale Strahlradius, der an der Taille des Strahls (also bei z=0 ) vorliegt, wird mit w_0 bezeichnet. In Abhängigkeit vom Abstand entlang der Achse verhält sich der Strahlradius dann im Nahfeld gemäß

$w(z)=w_{0}\,{\sqrt {1+{\left({\frac {z}{z_{R}}}\right)}^{2}}}$

mit der Rayleigh-Länge

$z_{R}={\frac {\pi \cdot w_{0}^{2}}{\lambda }}$ .

Axiales Profil

Im Abstand der Rayleighlänge von der Strahltaille ist der Strahl auf

$w(\pm z_{R})=w_{0}{\sqrt {2}}$

verbreitert. Die Rayleighlänge ist folglich der Abstand, bei dem sich die Strahlfläche in Bezug auf die kleinste Taille verdoppelt hat.

Der Abstand zwischen dem linken und rechten Punkt mit $|z|=z_{R}$ wird bi- oder konfokaler Parameter genannt:

$b=2z_{R}={\frac {2\pi w_{0}^{2}}{\lambda }}$

Damit ist die Amplitude $|E(0,z_{R})|=E_{0}{\tfrac {w_{0}}{w(z_{R})}}={\tfrac {1}{\sqrt {2}}}\,E_{0}$ also an einer bestimmten z-Koordinate auf das ${\tfrac {1}{{\sqrt {2}}}}$ -fache abgefallen. Dies entspricht einem Lorentz-Profil.

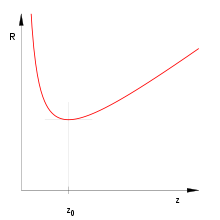
Krümmung

Radius der Wellenfronten über der Ausbreitungsrichtung. Für $z\rightarrow 0$ wird der Krümmungsradius unendlich, für großes z ergibt sich eine proportionale Abhängigkeit. Der kleinste Krümmungsradius liegt bei $z_{R}$ .

Die Exponentialfunktionen mit imaginären Exponenten bestimmen die Phasenlage der Welle bei (r,z) . Dabei bestimmt der Parameter R(z) anschaulich, wie stark die Phase an achsfernen Punkten verzögert ist, also, wie stark die Wellenfronten gekrümmt sind, und heißt deshalb Krümmungsradius. Er berechnet sich zu

$R(z)=z\,\left(1+{\left({\frac {z_{R}}{z}}\right)}^{2}\right)$ .

Direkt in der Strahltaille für z=0 ist der Krümmungsradius unendlich und es liegen ebene Wellenfronten vor. Im Vergleich zur ebenen homogenen Welle ist jedoch das Intensitätsprofil senkrecht zur Ausbreitungsrichtung nicht konstant, weshalb der Strahl außerhalb der Taille divergiert und die Wellenfronten sich krümmen.

Divergenz

Betrachtet man den Verlauf von w(z) für $z\gg z_{R}$ , nähert er sich einer Geraden – dies zeigt die Verbindung zur Strahlenoptik auf. Wie stark der Gauß-Strahl verläuft, sich also transversal ausdehnt, lässt sich dann durch den Winkel (genauer: 'Steigung', da wegen Strahlparameterprodukt $w_{0}\theta _{\mathrm {div} }={\tfrac {\lambda }{\pi }}M^{2}$ auch ${\mathrm {Winkel}}>\pi /2$ für kleine Strahltaillen w_0 möglich $\rightarrow \tan({\mathrm {Winkel}})$ ) zwischen dieser Geraden und der z-Achse angeben, dies nennt man die Divergenz:

$\theta _{\mathrm {div} }=\lim \limits _{z\rightarrow \infty }\arctan \left({\frac {w(z)}{z}}\right)\ \ =\ \ {\frac {w_{0}}{z_{R}}}$

Diese Beziehung führt zu dem Effekt, dass die Divergenz bei starker Fokussierung größer wird: Ist die Strahltaille schmal, verläuft der Strahl in großen Entfernungen stark auseinander. Man muss also einen Kompromiss aus Fokussierung und Reichweite finden.

Gouy-Phase

Ein Term der Wellenphase des Gauß-Strahls wird Gouy-Phase genannt:

$\zeta (z)=\arctan \left({\frac {z}{z_{R}}}\right)$

Der Phasenunterschied von $\pi$ der Grundmode beim Übergang von $z\ll 0$ zu $z\gg 0$ entspricht dem Umklappen im Fokus nach der klassischen Strahlenoptik.

Beim vollständigen Durchgang des Gauß-Bündels durch seine Taille erfährt der paraxiale Strahl im Vergleich zur ebenen Welle $e^{-ikz}$ die entsprechend einer halben Wellenlänge geringere Phasenverschiebung im Fall der rotationssymmetrischen Grundmode.

Zuerst beobachtete Louis Georges Gouy experimentell im Jahre 1890 den zunächst überraschenden Effekt. Gauß-Bündel sind gemäß dem Fourier-Theorem eine Superposition von Neigungsmoden ebener Wellen. Die zur Bündelachse geneigten Spektralkomponenten propagieren – in z-Richtung gemessen – offenbar mit einer kleineren Phasenschiebung verglichen mit einer achsparallelen Welle. Das stetige Neigungsspektrum ergibt überlagert die beobachtete endliche Phasenreduktion.

Matrizenoptik

Wenn ein Gaußstrahl auf parabolische Linsen oder Spiegel fällt, ist der resultierende Strahl wieder ein Gaußstrahl. Damit lassen sich die Regeln der Matrizenoptik aus der geometrischen Optik vollständig übertragen. Definiert man den Parameter $q(z)=z+iz_{R}$ , so wirkt die ABCD-Matrix eines optischen Elementes auf ihn gemäß

$q_{1}(z)={\frac {Aq_{0}+B}{Cq_{0}+D}}$

Komplizierte Kombinationen von optischen Elementen lassen sich zu einer Matrix zusammenfassen. Dies vereinfacht die Berechnung der Strahlprofile bei Strahlengängen, beispielsweise beim Berechnen von Resonanzen optischer Resonatoren.

Herleitung

Als Ausgangspunkt dienen die Maxwell-Gleichungen, aus denen eine Wellengleichung für elektromagnetische Wellen hergeleitet werden kann:

$c^{2}\Delta {\vec E}({\vec x},t)={\ddot {{\vec E}}}({\vec x},t)$

Ein allgemeiner Ansatz zur Lösung dieser Gleichung lautet

${\vec E}({\vec x},t)={\vec e}E({\vec x})e^{{i\omega t}}$

mit der Polarisation ${\vec {e}}$ . Einsetzen des Ansatzes in die Wellengleichung liefert die Helmholtzgleichung für die skalare Amplitude der Welle

$\Delta E({\vec x})=-k^{2}E({\vec x})$

mit der Kreiswellenzahl $k = \omega / c$ . Eine Lösung dieser Gleichung wären bspw. die ebenen Wellen, diese haben aber das Problem, dass sie im gesamten Raum die gleiche Amplitude haben, während Laserstrahlen räumlich stark begrenzt sind. Es ist deswegen sinnvoll für die Feldstärke den Ansatz

$E({\vec x})=E_{0}X(x,z)Y(y,z)e^{{-ikz}}$

zu wählen. Dieser gibt in Ausbreitungsrichtung eine harmonische, räumliche Oszillation vor sowie zwei (bisher noch) beliebige Formen in transversaler Ebene (senkrecht zur Ausbreitungsrichtung). Dieser Ansatz gilt weiterhin für den gesamten Raum, es wird deswegen noch eine weitere Annahme getroffen, die sogenannte Paraxialnäherung (engl. slowly varying envelope approximation) der Helmholtzgleichung, bei der gilt

$k{\frac {\partial }{\partial z}}\gg {\frac {\partial ^{2}}{\partial z^{2}}},{\frac {\partial X}{\partial z}}{\frac {\partial Y}{\partial z}}$

mit der Bedeutung, dass sich das Profil des Strahls entlang der Ausbreitungsrichtung nur langsam ändert. Einsetzen des Ansatzes in die Helmholtzgleichung, Ausführen der Ableitung so weit wie möglich, Anwenden der Näherung (Terme mit mehr als einer z-Ableitung gleich null setzen) führt zu der Differentialgleichung

$Y{\frac {\partial ^{2}X}{\partial x^{2}}}+X{\frac {\partial ^{2}Y}{\partial y^{2}}}-2ikY{\frac {\partial X}{\partial z}}-2ikX{\frac {\partial Y}{\partial z}}=0$

die in zwei unabhängige Gleichungen separiert werden kann:

${\begin{aligned}\left({\frac {\partial ^{2}}{\partial x^{2}}}-2ik{\frac {\partial }{\partial z}}\right)X(x,z)&=0\\\left({\frac {\partial ^{2}}{\partial y^{2}}}-2ik{\frac {\partial }{\partial z}}\right)Y(y,z)&=0\end{aligned}}$

Lösungen dieser Gleichungen lauten

${\begin{aligned}X_{m}(x,z)&={\sqrt {{\frac {w_{0}}{w(z)}}}}H_{m}\left({\frac {{\sqrt {2}}x}{w(z)}}\right)\exp \left(-{\frac {x^{2}}{w^{2}(z)}}-i{\frac {kx^{2}}{2R(z)}}+i{\frac {2m+1}{2}}\zeta (z)\right)\\Y_{n}(y,z)&={\sqrt {{\frac {w_{0}}{w(z)}}}}H_{n}\left({\frac {{\sqrt {2}}y}{w(z)}}\right)\exp \left(-{\frac {y^{2}}{w^{2}(z)}}-i{\frac {ky^{2}}{2R(z)}}+i{\frac {2n+1}{2}}\zeta (z)\right)\end{aligned}}$

wobei $H_{m}$ und $H_{n}$ die Hermite-Polynome sind. Diese Lösungen stellen die verschiedenen transversalen Moden eines Laserstrahls dar. Der Gauß-Strahl ist die Lösung für m=n=0 , für die die Hermite-Polynome Eins sind. Verwenden von Zylinderkoordinaten und Einsetzen der Lösungen in den Ansatz liefert die eingangs angeführte Feldverteilung: die TEM₀₀-Mode oder Gauß-Strahl.

Literatur

Dieter Meschede: Optik, Licht und Laser. 2. Auflage. B. G. Teubner, München 2005, ISBN 3-519-13248-6.
Eugene Hecht: Optik. 4. Auflage. Oldenbourg Wissenschaftsverlag, München 2005, ISBN 3-486-27359-0.

Basierend auf einem Artikel in:

Wikipedia.de