Cauchy-Verteilung

Die Cauchy-Verteilung (nach Augustin Louis Cauchy) ist eine stetige, leptokurtische (supergaußförmige) Wahrscheinlichkeitsverteilung.

Sie tritt in der Physik in der genäherten Beschreibung von Resonanzen auf, und wird dort Resonanzkurve oder Lorentzkurve (nach Hendrik Antoon Lorentz) genannt. Daher gibt es auch die Bezeichnungen Lorentz-Verteilung und Cauchy-Lorentz-Verteilung.

Definition

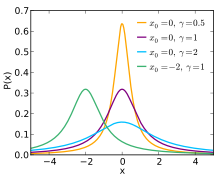
Dichtefunktion der Cauchy-Verteilung für verschiedene Werte der beiden Parameter. Dabei gilt: $\gamma$ im Bild entspricht s in der nebenstehenden Gleichung und $x_{0}$ entspricht t.

Die Cauchy-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeitsdichte

$f(x)={\frac {1}{\pi }}\cdot {\frac {s}{s^{2}+(x-t)^{2}}}\quad {\text{für}}-\infty <x<\infty$

mit s>0 und Lageparameter $-\infty <t<\infty$ besitzt.

Die Verteilungsfunktion der Cauchy-Verteilung ist

$F(x)=P(X\leq x)={\frac {1}{2}}+{\frac {1}{\pi }}\cdot \arctan \left({\frac {x-t}{s}}\right)$ .

Mit dem Zentrum t=0 und dem Breitenparameter s=1 ergibt sich die Standard-Cauchy-Verteilung (oder auch t-Verteilung mit einem Freiheitsgrad) mit

$f(x)={\frac {1}{\pi (1+x^{2})}}$

als Wahrscheinlichkeitsdichte und

$F(x)={\frac {1}{2}}+{\frac {1}{\pi }}\cdot \arctan(x)$

als Verteilungsfunktion.

Ist Cauchy-verteilt mit den Parametern und , dann ist ${\frac {X-t}{s}}$ standard-Cauchy-verteilt.

Eigenschaften

Erwartungswert, Varianz, Standardabweichung, Momente

Die Cauchy-Verteilung ist eine Verteilung, die weder Erwartungswert noch Varianz oder Standardabweichung besitzt, da die entsprechenden Integrale nicht endlich sind. Dementsprechend besitzt sie auch keine endlichen Momente und keine momenterzeugende Funktion.

Median, Modus, Quartilabstand

Die Cauchy-Verteilung besitzt den Median bei , den Modus ebenfalls bei , und den Quartilsabstand $2s$ .

Symmetrie

Die Cauchy-Verteilung ist symmetrisch zum Parameter .

Entropie

Die Entropie beträgt $\log(4\,\pi \,s)$ .

Charakteristische Funktion

Die charakteristische Funktion der Cauchy-Verteilung ist $y\mapsto \exp(ity-s|y|)$ .

Reproduktivität

Die Cauchy-Verteilung gehört zu den reproduktiven Wahrscheinlichkeitsverteilungen: der Mittelwert $(X_{1}+X_{2}+\dotsb +X_{n})/n$ aus standard-Cauchy-verteilten Zufallsvariablen ist selbst standard-Cauchy-verteilt. Insbesondere gehorcht die Cauchy-Verteilung also nicht dem Gesetz der großen Zahlen, das für alle Verteilungen mit existierendem Erwartungswert (siehe Satz von Etemadi) gilt.

Invarianz gegenüber Faltung

Die Cauchy-Verteilung ist invariant gegenüber Faltung, das heißt, die Faltung einer Lorentz-Kurve der Halbwertsbreite $\Gamma _{{a}}$ und einem Maximum bei $t_{a}$ mit einer Lorentz-Kurve der Halbwertsbreite $\Gamma _{{b}}$ und einem Maximum bei $t_{b}$ ergibt wieder eine Lorentz-Kurve mit der Halbwertsbreite $\Gamma _{{c}}=\Gamma _{{a}}+\Gamma _{{b}}$ und einem Maximum bei $t_{c}=t_{a}+t_{b}$ . Somit bildet die Cauchy-Verteilung eine Faltungshalbgruppe.

Beziehungen zu anderen Verteilungen

Beziehung zu stetigen Gleichverteilung

Ist auf dem Intervall $(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}})$ stetig gleichverteilt, dann ist $X=\tan(U)$ standard-Cauchy-verteilt.

Beziehung zur Normalverteilung

Der Quotient aus zwei unabhängigen standardnormalverteilten Zufallsvariablen ist standard-Cauchy-verteilt.

Beziehung zu studentschen t-Verteilung

Die Standard-Cauchy-Verteilung ist der Spezialfall der studentschen t-Verteilung mit einem Freiheitsgrad.

Beziehung zur Lévy-Verteilung

Die Cauchy-Verteilung ist eine spezielle α-stabile Verteilung mit dem Exponentenparameter $\alpha =1$ .

Anwendungsbeispiel

Bei der Cauchy-Verteilung als Vertreter der Heavy-tailed-Verteilungen ist die Wahrscheinlichkeit für extreme Ausprägungen sehr groß. Sind die 1 mindestens 2,326, so beträgt bei einer standard-Cauchy-verteilten Zufallsvariablen die entsprechende Untergrenze 31,82. Möchte man die Auswirkung von Ausreißern in Daten auf statistische Verfahren untersuchen, verwendet man häufig Cauchy-verteilte Zufallszahlen in Simulationen.

Zufallszahlen

Zur Erzeugung Cauchy-verteilter Zufallszahlen bietet sich die Inversionsmethode an. Die nach dem Simulationslemma zu bildende Pseudoinverse der Verteilungsfunktion F(x) lautet hierbei $F^{{-1}}(y)=-\cot(\pi y)$ (siehe Kotangens). Zu einer Folge von Standardzufallszahlen $u_{i}$ lässt sich daher durch $x_{i}:=-\cot(\pi u_{i})$ , oder wegen der Symmetrie auch durch $x_{i}:=\cot(\pi u_{i})$ , eine Folge standard-Cauchy-verteilter Zufallszahlen berechnen.

Basierend auf einem Artikel in:

Wikipedia.de