Median (Stochastik)

Der Median, auch Zentralwert genannt, ist in der Stochastik ein Lagemaß für Wahrscheinlichkeitsverteilungen und Verteilungen von Zufallsvariablen. Somit ist er wie auch der Erwartungswert und der Modus eine Kennzahl dafür, wo sich die "Mitte" einer Wahrscheinlichkeitsverteilung befindet. Anschaulich ist der Median die Zahl, bei der

die Wahrscheinlichkeit, einen Wert kleiner oder gleich dem Median zu erhalten und
die Wahrscheinlichkeit, einen Wert größer oder gleich dem Median zu erhalten

gleich ist. Es existieren mehrere Formalisierungen dieser intuitiven Vorstellung, die sich bezüglich der Existenz und Eindeutigkeit des Medians unterscheiden.

In der deskriptiven Statistik wird der Median für Stichproben definiert. Die beiden Begriffe unterscheiden sich insofern, als der eine Kennzahl einer Stichprobe ist (ähnlich dem arithmetischen Mittel), der andere eine Kennzahl einer Wahrscheinlichkeitsverteilung ist (ähnlich dem Erwartungswert). Die beiden sind per se verschieden, lassen aber über die empirische Verteilung verknüpfen.

Erste Definition

Für Wahrscheinlichkeitsverteilungen

Gegeben sei eine Wahrscheinlichkeitsverteilung auf $(\mathbb{R} ,{\mathcal B}(\mathbb{R} ))$ , also den reellen Zahlen, versehen mit der Borelschen σ-Algebra.

Dann heißt eine reelle Zahl ein Median (von ), wenn gilt:

$P((-\infty ,m])\geq {\tfrac {1}{2}}$ und $P([m,+\infty ))\geq {\tfrac {1}{2}}$ .

Für Zufallsvariablen

Gegeben sei eine reelle Zufallsvariable .

Dann heißt eine reelle Zahl ein Median (von ), wenn gilt:

$P(X\leq m)\geq {\tfrac {1}{2}}$ und $P(m\leq X)\geq {\tfrac {1}{2}}$ .

Damit ist der Median der Zufallsvariable genau der Median ihrer Verteilung $P_{X}$ .

Definition über Verteilungsfunktionen

Ebenso lässt sich der Median auch über Verteilungsfunktionen definieren. Ist die Verteilungsfunktion von oder von , so heißt ein Median (von oder von ), wenn

$F(m)\geq {\tfrac {1}{2}}\quad$ und $\quad \lim _{t\uparrow m}F(t)\leq {\tfrac {1}{2}}$ .

Hierbei bezeichnet $\lim _{t\uparrow m}F(t)$ den linksseitigen Grenzwert.

Bestimmung und Beispiele

Bei stetiger Verteilungsfunktion

Ist die Verteilungsfunktion stetig, so ist der Median eine Lösung der Gleichung

$F(m)={\tfrac {1}{2}}$

Dies beruht auf der Tatsache, dass der linksseitige Grenzwert dann mit dem Funktionswert übereinstimmt.

Beispiele

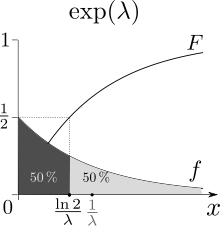
Median der Exponentialverteilung

Betrachtet man als Beispiel die Exponentialverteilung, so besitzt diese die Verteilungsfunktion

$F(x)={\begin{cases}1-\mathrm {e} ^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

für einen Parameter $\lambda >0$ . Gleichsetzen mit ${\tfrac {1}{2}}$ führt auf die Gleichung

${\tfrac {1}{2}}=\mathrm {e} ^{-\lambda m}$ ,

welche die Lösung

$m={\frac {\ln 2}{\lambda }}$

besitzt. In diesem Fall ist der Median eindeutig.

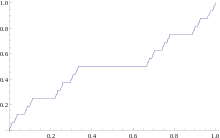
Plot der Cantorfunktion (10 Iterationen)

Aber auch bei stetiger Verteilungsfunktion kann der Median mehrdeutig sein. Betrachtet man beispielsweise die Cantor-Verteilung, deren Verteilungsfunktion rechts abgebildet ist, so nimmt diese aufgrund ihrer Konstruktion auf dem gesamten Intervall $[{\tfrac {1}{3}},{\tfrac {2}{3}})$ der Wert ${\tfrac {1}{2}}$ an. Jeder Punkt in diesem Intervall ist somit ein Median. Eindeutig ist der Median bei stetiger Verteilungsfunktion beispielsweise dann, wenn die Verteilungsfunktion streng monoton wachsend ist. Spezieller gilt die Eindeutigkeit bereits dann, wenn die Verteilungsfunktion in der einer Umgebung, in der sie den Wert ${\tfrac {1}{2}}$ annimmt, streng monoton wachsend ist.

Bei Wahrscheinlichkeitsdichten

Besitzt die Zufallsvariable beziehungsweise die Wahrscheinlichkeitsverteilung eine Wahrscheinlichkeitsdichtefunktion , (sie ist demnach eine Absolutstetige Verteilung), so ist der Median Lösung der Gleichung

$\int _{-\infty }^{m}f(x)\mathrm {d} x={\tfrac {1}{2}}$ .

Dies folgt direkt aus der Tatsache, dass absolutstetige Verteilungen immer eine stetige Verteilungsfunktion besitzen, diese sich über das Integral bestimmen lässt und der Aussage im obigen Abschnitt.

Mehrere Mediane treten hier beispielsweise auf, wenn die Wahrscheinlichkeitsdichtefunktion auf einem Interval konstant null ist.

Beispiel

Betrachtet man die Wahrscheinlichkeitsfunktion

$f(x)={\begin{cases}0&{\text{ falls }}\quad x\leq -1{\text{ oder }}x>1\\{\tfrac {1}{2}}&{\text{ falls }}\quad x\in (-1,-{\tfrac {1}{2}}]{\text{ oder }}x\in ({\tfrac {1}{2}},1]\\0&{\text{ falls }}\quad x\in (-{\tfrac {1}{2}},{\tfrac {1}{2}}]\\\end{cases}}$ ,

so ist diese im Interval $(-{\tfrac {1}{2}},{\tfrac {1}{2}})$ konstant Null. Über die elementaren Integrationsregeln folgt dann, dass jeder Wert in $[-{\tfrac {1}{2}},{\tfrac {1}{2}})$ ein Median ist. Das Lösen der Integralgleichung entspricht meist der Bestimmung der entsprechenden Verteilungsfunktion und kann damit als Spezialfall des Vorgehens im oberen Abschnitt angesehen werden.

Eindeutige Definition

Gegeben sei eine Wahrscheinlichkeitsverteilung oder eine reelle Zufallsvariable . Sei die Verteilungsfunktion von bzw. . Dann heißt

$m=\inf\{x\in \mathbb {R} \mid F(x)\geq {\tfrac {1}{2}}\}$

der Median von bzw. . Dies entspricht der folgenden Definition: Ist die Quantilfunktion zu , so ist der Median definiert als

$m:=Q({\tfrac {1}{2}})$ .

Wegen der Rechtsstetigkeit der Verteilungsfunktion kann bei der oberen der beiden Definitionen das Infumum auch durch ein Minimum ersetzt werden.

Eigenschaften

Bei dem Median handelt es sich um ein Quantil, genauer um das 50%-Quantil.

Ist die Verteilung symmetrisch, gilt also $P_{-X}=P_{X}$ , so ist Null ein Median. Allgemeiner ist bei jeder symmetrischen Verteilung die Symmetrieachse ein Median.

Jeder Median minimiert die absolute Abweichung, sprich ist eine Zufallsvariable mit $\operatorname {E} (|X|)<\infty$ , so gilt stets

$\operatorname {E} (|X-a|)\geq \operatorname {E} (|X-m|)$ für alle $a\in \mathbb {R}$

und Gleichheit gilt genau dann, wenn auch ein Median ist.

Beziehung zum Median der deskriptiven Statistik

Der Median in der deskriptiven Statistik (als Kennzahl einer Stichprobe) lässt sich über die empirische Verteilung mit dem Median einer Wahrscheinlichkeitsverteilung in Beziehung setzen: Ist eine Stichprobe $x=(x_{1},x_{2},\dots ,x_{n})$ gegeben, und ist $E_{x}$ die empirische Verteilung auf so ist ein Median (im Sinne der Wahrscheinlichkeitstheorie) von $E_{x}$ ein Median (im Sinne der deskriptiven Statistik) von . Aufgrund der verschiedenen Definitionen kann es jedoch auch zu leichten Abweichungen kommen.

Weitere Definitionen

Am direktesten wird der Median als derjenige Wert, für den

$P(X\leq m)={\frac {1}{2}}=P(X\geq m)$

gilt oder als $F^{-1}({\tfrac {1}{2}})$ definiert. In beiden Definitionen ist die Existenz des Medians aber nicht garantiert. So ist für

$P(X=0)=0{,}2=1-P(X=1)$

immer $F^{-1}({\tfrac {1}{2}})=\emptyset$ , da die Verteilungsfunktion nie den Wert ${\tfrac {1}{2}}$ annimmt. Ebenso existiert kein , so dass die obige Gleichungskette erfüllt ist: für alle $m<1$ ist $P(X\leq m)<{\tfrac {1}{2}}$ , ebenso wie für alle $m\geq 1$ immer $P(X\geq m)=1$ gilt.

Außerdem ist zu beachten, dass die Verteilungsfunktionen im älterer russischsprachiger Literatur als linksstetig und nicht wie im deutschen Sprachraum als rechtsstetig definiert werden. So ist dann zum Beispiel im Falle des fairen Münzwurfes einmal $F^{-1}({\tfrac {1}{2}})=(0,1]$ anstelle von $F^{-1}({\tfrac {1}{2}})=[0,1)$ .

Basierend auf einem Artikel in:

Wikipedia.de