Wahrscheinlichkeitsfunktion

Eine Wahrscheinlichkeitsfunktion, auch Zähldichte genannt, ist eine spezielle reellwertige Funktion in der Stochastik. Wahrscheinlichkeitsfunktionen werden zur Konstruktion und Untersuchung von Wahrscheinlichkeitsverteilungen, genauer diskreten Wahrscheinlichkeitsverteilungen verwendet. Dabei kann jeder diskreten Wahrscheinlichkeitsverteilung eine eindeutige Wahrscheinlichkeitsfunktion zugeordnet werden. Umgekehrt definiert jede Wahrscheinlichkeitsfunktion eine eindeutig bestimmte diskrete Wahrscheinlichkeitsverteilung.
In den meisten Fällen werden Wahrscheinlichkeitsfunktionen auf den natürlichen Zahlen
definiert. Sie ordnen dann jeder Zahl die Wahrscheinlichkeit
zu, dass diese Zahl auftritt. So würde bei der Modellierung eines fairen Würfels
die Wahrscheinlichkeitsfunktion den Zahlen von eins bis sechs jeweils den Wert
zuordnen und allen anderen die null.
Aus der Sicht der Maßtheorie handelt es sich bei Wahrscheinlichkeitsfunktionen um spezielle Dichtefunktionen (im Sinne der Maßtheorie) bezüglich des Zählmaßes. Diese werden im allgemeineren Kontext auch Gewichtsfunktionen genannt.
Definition
Definition Wahrscheinlichkeitsfunktion: Für eine diskrete Zufallsvariable
ist die Wahrscheinlichkeitsfunktion
für
definiert durch
Zur Konstruktion von Wahrscheinlichkeitsverteilungen
Gegeben sei eine Funktion
,
für die gilt
- Es ist
für alle
.
ordnet also jeder natürlichen Zahl eine reelle Zahl zwischen null und eins zu.
ist normiert in dem Sinne, dass sich die Funktionswerte zu eins aufsummieren. Es gilt also
-
.
Dann heißt
eine Wahrscheinlichkeitsfunktion und definiert durch
für alle
eine eindeutig bestimmte Wahrscheinlichkeitsverteilung
auf den natürlichen Zahlen
,
versehen mit der Potenzmenge
als Ereignissystem.
Aus Wahrscheinlichkeitsverteilungen abgeleitet
Gegeben sei eine Wahrscheinlichkeitsverteilung
auf den natürlichen Zahlen
,
versehen mit
,
und sei
eine Zufallsvariable
mit Werten in
.
Dann heißt
definiert durch
die Wahrscheinlichkeitsfunktion von .
Analog heißt
definiert durch
die Wahrscheinlichkeitsfunktion von
Beispiele
Eine typische Wahrscheinlichkeitsfunktion ist
für eine natürliche Zahl
und eine reelle Zahl
.
Die Normiertheit folgt hier direkt aus dem binomischen
Lehrsatz, denn es ist
.
Die so erzeugte Wahrscheinlichkeitsverteilung ist die Binomialverteilung.
Eine weitere klassische Wahrscheinlichkeitsfunktion ist
für
und ein .
Hier folgt die Normiertheit aus der geometrischen
Reihe, denn es ist
.
Die so erzeugte Wahrscheinlichkeitsverteilung ist die Geometrische Verteilung.
Allgemeine Definition
Die Definition lässt sich von den natürlichen Zahlen auf beliebige höchstens
abzählbare Mengen ausweiten. Ist
solch eine Menge und ist
mit
,
so definiert
durch
für alle
eine eindeutig bestimmte Wahrscheinlichkeitsverteilung auf .
Ist umgekehrt
eine Wahrscheinlichkeitsverteilung auf
und
eine Zufallsvariable mit Werten in
,
so heißen
definiert durch
und
definiert durch
die Wahrscheinlichkeitsfunktion von
beziehungsweise
.
Alternative Definition
Manche Autoren definieren zuerst reelle Folgen
mit
für alle
und
und nennen diese Folgen Wahrscheinlichkeitsvektoren oder stochastische Folgen.
Eine Wahrscheinlichkeitsfunktion wird dann definiert als
gegeben durch
für alle
Umgekehrt definiert dann jede Wahrscheinlichkeitsverteilung oder
Zufallsvariable auf
auch eine stochastische Folge/Wahrscheinlichkeitsvektor über
beziehungsweise
Andere Autoren nennen bereits die Folge
eine Zähldichte.
Weitere Beispiele
Typisches Beispiel für Wahrscheinlichkeitsfunktionen auf beliebigen Mengen
ist die diskrete
Gleichverteilung auf einer endlichen Menge .
Sie besitzt dann per Definition die Wahrscheinlichkeitsfunktion
für alle
.
Der Zugang über die stochastischen Folgen erlaubt die folgende Konstruktion
von Wahrscheinlichkeitsfunktionen: Ist eine beliebige (höchstens abzählbare)
Folge von positiven reellen Zahlen
mit Indexmenge
gegeben, für die
gilt, so definiert man
.
Dann ist
eine stochastische Folge und definiert damit auch eine
Wahrscheinlichkeitsfunktion. Betrachtet man zum Beispiel die Folge
für
,
so ist
.
Somit ist die Normierungskonstante
und als Wahrscheinlichkeitsfunktion ergibt sich
.
Dies ist die Wahrscheinlichkeitsfunktion der Poisson-Verteilung.
Bestimmung von Kennzahlen durch Wahrscheinlichkeitsfunktionen
Viele der wichtigen Kennzahlen von Zufallsvariablen und Wahrscheinlichkeitsverteilungen lassen sich bei Existenz der Wahrscheinlichkeitsfunktion direkt aus dieser herleiten.
Erwartungswert
Ist
eine Zufallsvariable mit Werten in
und Wahrscheinlichkeitsfunktion
,
so ist der Erwartungswert
gegeben durch
.
Er existiert immer, kann aber auch unendlich sein. Ist allgemeiner
eine höchstens abzählbare Teilmenge der reellen Zahlen und
eine Zufallsvariable mit Werten in
und Wahrscheinlichkeitsfunktion
so ist der Erwartungswert gegeben durch
falls die Summe existiert.
Varianz
Analog zum Erwartungswert lässt sich auch die Varianz direkt aus der Wahrscheinlichkeitsfunktion herleiten. Sei dazu
der Erwartungswert. Ist dann
eine Zufallsvariable mit Werten in
und Wahrscheinlichkeitsfunktion
,
so ist die Varianz gegeben durch
oder aufgrund des Verschiebungssatzes äquivalent dazu
Entsprechend gilt im allgemeineren Fall einer Zufallsvariable mit Werten in
(vgl. oben), dass
Auch hier gelten alle Aussagen nur, wenn die entsprechenden Summen existieren.
Modus
Für diskrete Wahrscheinlichkeitsverteilungen
wird der Modus direkt über
die Wahrscheinlichkeitsfunktion definiert: Ist
eine Zufallsvariable mit Werten in
und Wahrscheinlichkeitsfunktion
oder ist
eine Wahrscheinlichkeitsverteilung auf
mit Wahrscheinlichkeitsfunktion
,
so heißt
ein Modus oder Modalwert von
oder
,
wenn
ist. Ist etwas allgemeiner eine höchstens
abzählbare Menge
gegeben, deren Elemente
in aufsteigender Ordnung sortiert sind, das heißt
,
so heißt ein
ein Modus oder Modalwert, wenn
gilt.
Eigenschaften und aufbauende Begriffe
Verteilungsfunktionen und Wahrscheinlichkeitsfunktionen
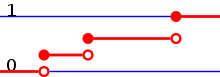
Ist
eine Wahrscheinlichkeitsfunktion auf
,
so ist die Verteilungsfunktion
des entsprechenden Wahrscheinlichkeitsmaßes gegeben als
.
Dabei bezeichnet
die Abrundungsfunktion,
das heißt
ist größte ganze Zahl, die kleiner oder gleich
ist.
Ist
auf einer höchstens abzählbaren Teilmenge der reellen Zahlen definiert, also auf
,
so ist die Verteilungsfunktion des Wahrscheinlichkeitsmaßes definiert durch
.
Beispiel hierfür ist .
Faltung und Summe von Zufallsvariablen
Für Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsfunktionen kann
die Faltung
(von Wahrscheinlichkeitsverteilungen) auf die Faltung (von
Funktionen) der entsprechenden Wahrscheinlichkeitsfunktionen zurückgeführt
werden. Sind
Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsfunktionen
und
,
so ist
.
Hierbei bezeichnet
die Faltung von
und
und
die Faltung der Funktionen
und
.
Die Wahrscheinlichkeitsfunktion der Faltung zweier
Wahrscheinlichkeitsverteilungen ist somit genau die Faltung der
Wahrscheinlichkeitsfunktionen der Wahrscheinlichkeitsverteilungen.
Diese Eigenschaft überträgt sich direkt auf die Summe von stochastisch
unabhängigen Zufallsvariablen. Sind zwei stochastisch unabhängige
Zufallsvariablen
mit Wahrscheinlichkeitsfunktionen
und
gegeben, so ist
.
Die Wahrscheinlichkeitsfunktion der Summe ist somit die Faltung der Wahrscheinlichkeitsfunktionen der einzelnen Zufallsvariablen.
Wahrscheinlichkeitserzeugende Funktion
Auf
lässt sich jeder Wahrscheinlichkeitsverteilung eine
wahrscheinlichkeitserzeugende Funktion zuordnen. Dies ist ein Polynom oder eine Potenzreihe mit der
Wahrscheinlichkeitsfunktion als Koeffizienten. Sie ist somit definiert als
für die Wahrscheinlichkeitsfunktion
einer Wahrscheinlichkeitsverteilung
.
Die wahrscheinlichkeitserzeugende Funktion einer Zufallsvariable wird analog
definiert.
Wahrscheinlichkeitserzeugende Funktionen erleichtern die Untersuchung von und das Rechnen mit Wahrscheinlichkeitsverteilungen. So ist beispielsweise die wahrscheinlichkeitserzeugende Funktion der Faltung zweier Wahrscheinlichkeitsverteilungen genau das Produkt der wahrscheinlichkeitserzeugenden Funktionen der einzelnen Wahrscheinlichkeitsverteilungen. Ebenso finden sich wichtige Kennzahlen wie der Erwartungswert und die Varianz in den Ableitungen der wahrscheinlichkeitserzeugenden Funktionen wieder.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.03. 2021