
Poisson-Verteilung
Die Poisson-Verteilung (benannt nach dem Mathematiker Siméon Denis Poisson) ist eine Wahrscheinlichkeitsverteilung, mit der die Anzahl von Ereignissen modelliert werden kann, die bei konstanter mittlerer Rate unabhängig voneinander in einem festen Zeitintervall oder räumlichen Gebiet eintreten. Sie ist eine univariate diskrete Wahrscheinlichkeitsverteilung, die einen häufig vorkommenden Grenzwert der Binomialverteilung für unendlich viele Versuche darstellt. Sie lässt sich aber auch aus grundlegenden Prozesseigenschaften axiomatisch herleiten.
Die Zuwächse eines Poisson-Prozesses sind Poisson-verteilte Zufallsvariablen. Erweiterungen der Poisson-Verteilung wie die Verallgemeinerte Poisson-Verteilung und die Gemischte Poisson-Verteilung werden vor allem im Bereich der Versicherungsmathematik angewendet.
Definition
Die Poisson-Verteilung
ist eine diskrete Wahrscheinlichkeitsverteilung. Sie wird durch einen reellen Parameter
bestimmt, der den Erwartungswert
und gleichzeitig die Varianz
der Verteilung beschreibt. Sie ordnet den natürlichen
Zahlen
die Wahrscheinlichkeiten
zu, wobei
die eulersche
Zahl und
die Fakultät
von
bezeichnet. Der Parameter
beschreibt anschaulich die bei einer Beobachtung erwartete Ereignishäufigkeit.
Die Poisson-Verteilung gibt dann die Wahrscheinlichkeit einer bestimmten
Ereignisanzahl
im Einzelfall an, wenn die mittlere
Ereignisrate
bekannt ist.
Eigenschaften
Verteilungsfunktion
Die Verteilungsfunktion
der Poisson-Verteilung ist
und gibt die Wahrscheinlichkeit
dafür an, höchstens
Ereignisse zu finden, wo man
im Mittel erwartet. Dabei bezeichnet
die regularisierte
Gammafunktion der unteren Grenze.
Erwartungswert, Varianz, Moment
Ist die Zufallsvariable
Poisson-verteilt, also
,
so ist
zugleich Erwartungswert
und Varianz,
denn es gilt
sowie
Nach der Verschiebungsformel folgt nun:
Auch für das dritte zentrierte Moment gilt .
Median
Es liegt die Vermutung nahe, dass der Median
nahe bei
liegt. Eine exakte Formel existiert jedoch nicht, die genauest mögliche
Abschätzung ist
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man sofort den Variationskoeffizienten
.
Schiefe und Wölbung
Die Schiefe ergibt sich zu
.
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
.
Höhere Momente
Das k-te Moment
lässt sich als Polynom von Grad k in
angeben und ist das k-te vollständige
Bell-Polynom
ausgewertet an den k Stellen
:
.
Kumulanten
Die kumulantenerzeugende Funktion der Poisson-Verteilung ist
.
Damit sind alle Kumulanten
gleich
Charakteristische Funktion
Die charakteristische Funktion hat die Form
.
Wahrscheinlichkeitserzeugende Funktion
Für die wahrscheinlichkeitserzeugende Funktion erhält man
.
Momenterzeugende Funktion
Die momenterzeugende Funktion der Poisson-Verteilung ist
>Reproduktivität
Die Poisson-Verteilung ist reproduktiv,
d.h., die Summe
stochastisch
unabhängiger Poisson-verteilter Zufallsvariabler
mit den Parametern
ist wieder Poisson-verteilt mit dem Parameter
.
Für die Faltung
gilt also
Somit bilden die Poisson-Verteilungen eine Faltungshalbgruppe. Dieses Ergebnis folgt unmittelbar aus der charakteristischen Funktion der Poisson-Verteilung und der Tatsache, dass die charakteristische Funktion einer Summe unabhängiger Zufallsvariablen das Produkt der charakteristischen Funktionen ist.
Die Poisson-Verteilung ist also auch unendlich
teilbar. Nach einem Satz des sowjetischen
Mathematikers D. A. Raikow gilt auch die Umkehrung: Ist eine
Poisson-verteilte Zufallsvariable
die Summe von zwei unabhängigen Zufallsvariablen
und
,
dann sind die Summanden
und
ebenfalls Poisson-verteilt. Eine Poisson-verteilte Zufallsvariable lässt sich
also nur in Poisson-verteilte unabhängige Summanden zerlegen. Dieser Satz ist
ein Analogon zu dem Satz
von Cramér für die Normalverteilung.
Ausdünnung
Häufig kommen stochastische Experimente vor, bei denen die Ereignisse
eigentlich Poisson-verteilt sind, aber die Zählung nur erfolgt, wenn noch eine
zusätzliche Bedingung erfüllt ist. Beispielsweise könnte die Anzahl der Eier,
die ein Insekt legt, Poisson-verteilt sein, aber aus jedem Ei schlüpft nur mit
einer bestimmten Wahrscheinlichkeit eine Larve. Ein Beobachter dieser
Poisson-verteilten Zufallsvariable mit Parameter
zählt jedes Ereignis also nur mit einer Wahrscheinlichkeit
(unabhängig voneinander).
Alternativ könnte aber auch ein Fehler bei der Zählung dazu führen, dass das
Ereignis nicht registriert wird. Wenn also ursprünglich
Ereignisse vorliegen, werden entsprechend der Binomial-Verteilung
nur
Ereignisse gezählt. In diesem Fall ist der wahre Wert
unbekannt und variiert zwischen dem gemessenen Wert
(alle vorhandenen Ereignisse gesehen) und unendlich (es gab mehr Ereignisse, als
gesehen wurden). Die Wahrscheinlichkeit eines Messwertes
findet man dann mittels des Produktes der Wahrscheinlichkeit einer erfolgreichen
Messung
und der ursprünglichen Poisson-Verteilung
,
summiert über alle möglichen Werte
:
.
Die gefundenen Werte
bei Nachweiswahrscheinlichkeit
sind also wieder Poisson-verteilt. Die Nachweiswahrscheinlichkeit
reduziert den Parameter
der ursprünglichen Poisson-Verteilung zu
.
Dies bezeichnet man auch als Ausdünnung der Poisson-Verteilung.
Berechnung
Die Berechnung von
kann folgendermaßen rekursiv erfolgen. Zuerst bestimmt man
,
dann ergeben sich nacheinander
.
Mit wachsendem
werden dabei die Wahrscheinlichkeiten größer, solange
ist. Wird
,
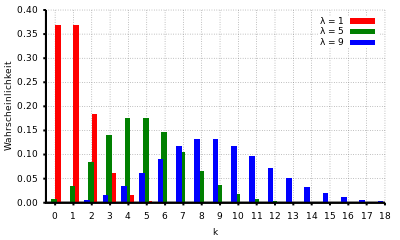
schrumpfen sie. Der Modus,
also der Wert mit der größten Wahrscheinlichkeit, beträgt
,
wenn
nicht ganzzahlig ist, anderenfalls gibt es zwei benachbarte
(siehe Diagramm rechts oben).
Falls die Berechnung von
wegen zu großer Werte von
und
Probleme bereitet, dann kann folgende mit der Stirlingformel
erhaltene Näherung weiterhelfen:
Poisson-verteilte Zufallszahlen werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.
Parameterschätzung
Maximum-Likelihood-Schätzer
Aus einer Stichprobe von
Beobachtungen
für
soll der Parameter
der Poisson-verteilten Grundgesamtheit geschätzt werden. Der Maximum-Likelihood-Schätzer
ist gegeben durch das arithmetische
Mittel
.
Der Maximum-Likelihood-Schätzer ist ein unverzerrter, effizienter und
suffizienter Schätzer für den Parameter .
Konfidenzintervall
Das Konfidenzintervall
für
erhält man aus der Beziehung zwischen Poisson- und Chi-Quadrat-Verteilung.
Liegt ein Stichprobenwert
vor, dann ist ein Konfidenzintervall für
zum Konfidenzniveau
gegeben durch
,
wobei
die Quantilfunktion
der Chi-Quadrat-Verteilung mit
Freiheitsgraden bezeichnet.
Prognoseintervall
Das Prognoseintervall
hat die Aufgabe, vor dem Ziehen einer Stichprobe einen Bereich vorherzusagen, in
dem man die Realisierung einer Schätzfunktion mit hoher Wahrscheinlichkeit
findet. Die Anzahl
Poisson-verteilter Ereignisse, die mit vorgegebener Wahrscheinlichkeit
nicht überschritten wird, lässt sich aus der Inversion
der Verteilungsfunktion
berechnen:
Dabei lässt sich wieder
durch die regularisierte Gammafunktion
ausdrücken. Eine elementare Form der Inversion der Verteilungsfunktion
oder der Gammafunktion ist nicht bekannt. Gute Dienste leistet in diesem Fall
eine zweispaltige
Wertetabelle, die leicht mit der oben im Abschnitt Verteilungsfunktion
angegebenen Summe berechenbar ist und zeigt, welche Wahrscheinlichkeiten
bestimmten Werten von
zugeordnet sind.
Beziehung zu anderen Verteilungen
Beziehung zur Binomialverteilung
Ebenso wie die Binomialverteilung
sagt die Poisson-Verteilung das zu erwartende Ergebnis einer Serie von Bernoulli-Experimenten
voraus. Letzteres sind Zufallsexperimente,
die nur zwei mögliche Ergebnisse kennen (zum Beispiel „Erfolg“ und
„Misserfolg“), also einen dichotomen
Ereignisraum
besitzen. Wird das zeitliche oder räumliche Beobachtungsintervall immer weiter
unterteilt, erhöht sich damit die Zahl der Versuche.
Die fortschreitende Unterteilung bedingt eine Abnahme der
Erfolgswahrscheinlichkeit
derart, dass das Produkt
gegen einen endlichen Grenzwert
konvergiert.
Dementsprechend nähert sich die binomiale Wahrscheinlichkeitsverteilung der
mathematisch etwas einfacheren Poisson-Verteilung an.
Die Poisson-Verteilung lässt sich aus der Binomialverteilung herleiten. Sie
ist die Grenzverteilung der Binomialverteilung bei sehr kleinen Anteilen der
interessierenden Merkmale und sehr großem Stichprobenumfang:
und
unter der Nebenbedingung, dass das Produkt
einen Wert annimmt, der weder null noch unendlich ist.
ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie
auch für die resultierende Poisson-Verteilung der Erwartungswert.
Sowohl die Poisson-Verteilung, als auch die Binomialverteilung sind Spezialfälle der Panjer-Verteilung.
Beziehung zur verallgemeinerten Binomialverteilung
Auch die verallgemeinerte Binomialverteilung kann für große Stichproben und kleine Erfolgswahrscheinlichkeiten mittels der Poisson-Approximation angenähert werden.
Beziehung zur Normalverteilung
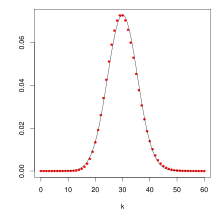
Die Poisson-Verteilung
hat für kleine Werte von
eine stark asymmetrische Gestalt. Für größer werdendes
wird
symmetrischer und ähnelt ab etwa
einer gaußschen Normalverteilung
mit
und
:
Beziehung zur Erlang-Verteilung
- In einem Poisson-Prozess
genügt die zufällige Anzahl der Ereignisse in einem festgelegten Intervall der
Poisson-Verteilung
. Der zufällige Abstand (Strecke oder Zeit) bis zum Eintreffen des
-ten Ereignisses sowie der Abstand zwischen den Ereignissen
und
sind hingegen
Erlang-verteilt. Man sagt auch, dass die Poisson-Verteilung und die Erlang-Verteilung zueinander konjugierte Verteilungen sind. Im Fall
geht diese Erlang-Verteilung in eine Exponentialverteilung über
. Dabei bezeichnet
die Zahl der erwarteten Ereignisse pro Einheitsintervall.
ist dann die Verteilungsdichte des Abstands
, der bis zum Eintreffen des nächsten Ereignisses vergehen wird, wie auch des Abstandes zwischen zwei aufeinanderfolgen Ereignissen.
- Für die Verteilungsfunktionen der Erlang-Verteilung und der Poisson-Verteilung gilt
.
Beziehung zur Chi-Quadrat-Verteilung
Die Verteilungsfunktionen der Poisson-Verteilung
und der Chi-Quadrat-Verteilung
mit
Freiheitsgraden
hängen auf folgende Weise zusammen:
Die Wahrscheinlichkeit,
oder mehr Ereignisse in einem Intervall zu finden, innerhalb dessen man im
Mittel
Ereignisse erwartet, ist gleich der Wahrscheinlichkeit, dass der Wert von
ist. Es gilt also
.
Dies folgt aus
mit
und
als regularisierte Gammafunktionen.
Beziehung zur Skellam-Verteilung
Dagegen ist die Differenz
zweier stochastisch
unabhängiger Poisson-verteilter Zufallsvariablen
und
mit den Parametern
und
nicht wieder Poisson-verteilt, sondern Skellam-verteilt.
Es gilt:
,
wobei
die modifizierte
Bessel-Funktion bezeichnet.
Weitere Poisson-Verteilungen
Einige weitere Verteilungen tragen teilweise den Namen „Poisson“ und sind Verallgemeinerungen der hier beschriebenen Poisson-Verteilung:
- Die verallgemeinerte Poisson-Verteilung ist eine diskrete Verteilung mit zwei Formparametern. Setzt man einen von ihnen gleich Null, ergibt sich wieder die gewöhnliche Poisson-Verteilung.
- Die gemischte Poisson-Verteilung kombiniert die Poisson-Verteilung mit einer weiteren Wahrscheinlichkeitsdichte.
- Die Poisson-Gamma-Verteilung entsteht bei Kombination mit der Gamma-Verteilung. Sie entspricht der negativen Binomialverteilung.
- Eine weitere Verallgemeinerung ist die zusammengesetzte Poisson-Verteilung. Sie entsteht, wenn man eine Summe unabhängig identisch verteilter Zufallsvariablen bildet und die Anzahl der Summanden Poisson-verteilt ist. Im Gegensatz zu den meisten Verteilungen ist bei dieser Verteilung nicht festgelegt, ob sie stetig oder diskret ist. Sind die aufsummierten Zufallsvariablen logarithmisch verteilt, so erhält man die negative Binomialverteilung und als einen Spezialfall davon auch die geometrische Verteilung.
Freie Poisson-Verteilung
In der freien
Wahrscheinlichkeitstheorie gibt es ein freies Analogon zur
Poisson-Verteilung, die freie
Poisson-Verteilung. Sie wird in Analogie zu einem
entsprechenden Grenzwertsatz
für die Poisson-Verteilung als der Grenzwert
der iterierten freien Faltung
für
definiert.
Bivariate Poisson-Verteilung
Die bivariate Poisson-Verteilung wird definiert durch
Die Randverteilungen sind Poisson-verteilt mit den Parametern
und
und es gilt
.
Die Differenz ist Skellam-verteilt mit den Parametern
und
.
Dies bedeutet, dass man relativ einfach Abhängigkeiten zwischen
Poisson-verteilten Zufallsvariablen einführen kann, wenn man die Mittelwerte der
Randverteilungen sowie die Kovarianz kennt oder schätzen kann. Man kann dann die
bivariate Poisson-Verteilung
einfach erzeugen, indem man drei unabhängige Poisson-verteilte Zufallsvariablen
definiert mit Parametern
und dann
setzt.
Analog kann die multivariate Poisson-Verteilung definiert werden.
Anwendungsbeispiele
„Seltene“ Ereignisse
Das klassische Beispiel stammt von Ladislaus von Bortkewitsch, der bei der Untersuchung der Anzahlen der Todesfälle durch Hufschlag in den einzelnen Kavallerie-Einheiten der preußischen Armee pro Jahr belegen konnte, dass diese Anzahlen gut durch eine Poisson-Verteilung beschrieben werden können.
Allgemein müssen für die einzelnen Zählereignisse (im Beispiel die einzelnen Todesfälle durch Hufschläge) die folgenden Bedingungen gelten, damit die Anzahl Poisson-verteilt ist:
- Einzelereignisse: Die Wahrscheinlichkeit, dass zwei Ereignisse in einem kurzen Zeitraum auftreten, ist vernachlässigbar.
- Proportionalität: Die Wahrscheinlichkeit, ein Ereignis in einem kurzen Zeitraum zu beobachten, ist proportional zur Länge des Zeitraums.
- Homogenität: Die Wahrscheinlichkeit, ein Ereignis in einem kurzen Zeitraum zu beobachten, ist unabhängig von der Lage des Zeitraums.
- Unabhängigkeit: Die Wahrscheinlichkeit, ein Ereignis in einem kurzen Zeitraum zu beobachten, ist unabhängig von der Wahrscheinlichkeit eines Ereignisses in anderen nicht-überlappenden Zeiträumen.
Alternativ kann man diese Bedingungen auch damit erklären, dass die Wartezeit zwischen zwei Ereignissen exponentialverteilt ist. Da diese gedächtnislos ist, treten die Ereignisse quasi zufällig und unabhängig voneinander ein.
Es ist in jedem Einzelfall zu prüfen, ob die Bedingungen vorliegen, aber typische Beispiele sind:
- Anzahl der Druckfehler auf einer Buchseite
- Anzahl der ankommenden Gespräche pro Stunde in einer Telefonzentrale
- Anzahl der radioaktiven Zerfälle einer Substanz in einem gegebenen Zeitintervall (vorausgesetzt, dass die Zerfallsrate nicht merklich abnimmt, die Messdauer also klein im Vergleich zur Halbwertszeit ist)
- Anzahl der Blitzeinschläge pro ha und Jahr
- Anzahl der aufgetretenen Impfschäden pro Jahr
- die Bombardierung von London
Nach dem Satz von Palm-Chintschin konvergieren sogar allgemeine Erneuerungsprozesse unter relativ milden Bedingungen gegen einen Poisson-Prozess, d.h., auch hier ergibt sich für die Anzahl der Ereignisse wieder die Poisson-Verteilung. Das bedeutet, dass die oben angegebenen Bedingungen noch erheblich abgeschwächt werden können.
Ankünfte von Kunden
In Warteschlangensystemen kommen Kunden oder Aufträge im System an, um bedient zu werden. In der Warteschlangentheorie werden die unterschiedlichen Modelle in der Kendall-Notation beschrieben. Dabei werden häufig insb. die Anzahl der Kunden, die in einem gewissen Zeitintervall ankommen, mit einer Poisson-Verteilung modelliert (abgekürzt durch M für exponentialverteilte Zwischenankunftszeiten). Diese Modellbildung ist sehr attraktiv, da sich unter dieser Annahme oft einfache analytische Lösungen ergeben.
Häufig kann diese Annahme auch näherungsweise gerechtfertigt werden, hier
soll an einem Beispiel illustriert werden, was diese Annahme bedeutet: Ein
Kaufhaus wird beispielsweise an einem Samstag durchschnittlich alle 10 Sekunden
von einem Kunden betreten. Werden nun im Takt von einer Minute die Personen
gezählt, die neu dazu kamen, so würde man im Mittel 6 Personen erwarten, die das
Kaufhaus pro Minute betreten. Die Wahl der Länge des Intervalls liegt beim
Beobachter. Würde man eine Stunde als Beobachtungsintervall wählen, ergäbe sich
,
bei einem Intervall von 1 Sekunde wäre
.
Die relative Schwankung der Kundenanzahl (
)
nimmt mit größer werdendem Intervall und folglich größer werdendem
ab. Das längere Intervall erlaubt also über die längere Mittelung eine im
Prinzip präzisere Beobachtung, ist aber mit mehr Aufwand verbunden und kann
innerhalb des Intervalls auftretende Veränderung der Bedingungen (z.B.
Ankunft eines Busses mit einkaufswilligen Touristen) nicht erfassen.
Unter folgenden Randbedingungen könnte eine Poissonverteilung vorliegen:
- Die Kunden müssen einzeln ankommen. In der Realität kommen aber häufig Personengruppen gemeinsam an.
- Die Wahrscheinlichkeit, dass ein Kunde ankommt, könnte proportional zur Länge des Beobachtungszeitraums sein.
- Es gibt sicherlich über den Tag verteilt Stoßzeiten mit erhöhtem Kundenaufkommen, und Flauten.
- Die Kundenankünfte in verschiedenen Zeiträumen sind nicht notwendigerweise unabhängig. Z.B. bei Überfüllung des Kaufhauses könnten Kunden abgeschreckt werden.
In diesem Beispiel ist die Annahme der Poisson-Verteilung nur schwer zu rechtfertigen, daher gibt es Warteschlangenmodelle z.B. mit Gruppenankünften, endlichen Warteschlangen oder anderen Ankunftsverteilungen, um diesen Ankunftsprozess realistischer zu modellieren. Glücklicherweise sind einige wichtige Kennzahlen, wie z.B. nach Littles Gesetz die durchschnittliche Anzahl von Kunden im System, nicht von der konkreten Verteilung abhängig, d.h., auch wenn Annahmen verletzt sind, gilt dasselbe Ergebnis.
Ball-Fächer-Modell
Im Gebiet Abzählende
Kombinatorik besteht eine Standard-Aufgabe darin, Bälle oder Kugeln auf
Fächer zu verteilen und abzuzählen, wie viele Möglichkeiten es gibt. Ordnet man
die
Bälle den
Fächern zufällig zu, so erhält man für die Anzahl der Bälle in einem festen Fach
eine Binomialverteilung
mit
.
Eine Anwendung ist z.B. die Verteilung von Rosinen auf einem Kuchen, mit
dem Ziel, dass jedes Stück eine Mindestanzahl von Rosinen enthält.

Das Bild rechts zeigt einen Ausschnitt eines Fußbodens mit quadratischen
Fliesen, auf dem Reiskörner zufällig verstreut wurden. Die
Felder enthalten je
Reiskörner und insgesamt befinden sich
Reiskörner im betrachteten Ausschnitt. Man kann die Wahrscheinlichkeiten jetzt
direkt über die Binomialverteilung
bestimmen, aber es sind auch die Voraussetzungen der Poisson-Approximation
erfüllt.
Der Vergleich zwischen Experiment und berechneter Poisson-Verteilung ,
wobei
Reiskörner/Quadrate ist, zeigt intuitiv eine gute Übereinstimmung. Statistisch
könnte man die Güte mit einem Anpassungstest
überprüfen.
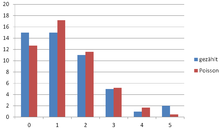
| gezählt | ||
|
0 |
15 |
12,7 |
|
1 |
15 |
17,2 |
|
2 |
11 |
11,6 |
|
3 |
5 |
5,2 |
|
4 |
1 |
1,7 |
|
5 |
2 |
0,5 |
Die Wahrscheinlichkeit, dass ein bestimmtes Feld leer bleibt, ist etwa 26 %:
Sportergebnisse
In vielen Sportarten geht es in einem Wettbewerb darum, innerhalb eines bestimmten Zeitraums mehr zählende Ereignisse zu erwirken als der Gegner. Der Physiker Metin Tolan hat in seinem Buch zum Fußballspiel die Anwendbarkeit der Poisson-Verteilung im Sport ausführlich untersucht.
Die (zeitliche) Konstanz der Ereigniswahrscheinlichkeit – eine hinreichende Voraussetzung für die Anwendung der Poisson-Statistik (siehe oben unter Poissonsche Annahmen) – ist bei Sportergebnissen in der Regel höchstens näherungsweise gegeben. Aber ist man nur an dem reinen Zählwert, z.B. der Torzahl einer Mannschaft, interessiert, so ergibt sich auch bei zeitabhängiger Torrate eine Poisson-Verteilung. Schwieriger zu rechtfertigen ist die oft getroffene Annahme, dass die Tor- oder Punktzahlen zweier Mannschaften unabhängig sind. Kann man diese Annahme nicht statistisch ausreichend begründen, z.B. durch Hypothesen- oder Anpassungstest auf Übereinstimmung der Daten mit der Poisson-Verteilung, so kann man beispielsweise zur bivariaten Poisson-Verteilung übergehen und durch Schätzung der Kovarianz eine Abhängigkeit einführen.
Metin Tolan begründet, dass man die Torzahl einer Mannschaft in einem Fußballspiel in guter Näherung als Poisson-verteilt annehmen darf. In seinem Ansatz berücksichtigt er zur Schätzung allerdings nur die durchschnittliche Anzahl von Toren pro Spiel und Mannschaft, d.h., er betrachtet beispielsweise nicht die Spielstärke der gegnerischen Mannschaft. Er hat auch nachgewiesen, dass über 70 % der Varianz der Punkteverteilung in der Fußball-Bundesliga durch Zufall erklärt werden können. Dies belegt auch aus stochastischer Sicht, warum Fußball spannend ist.
Für das Pokalendspiel 2015 hätte Tolan z.B. auf Grundlage der abgelaufenen Bundesliga-Saison für den VfL Wolfsburg 2,12 Tore und für Borussia Dortmund 1,38 Tore geschätzt. Andreas Heuer geht einen Schritt weiter und definiert die Spielstärke einer Mannschaft als die mittlere Tordifferenz einer Mannschaft beim Spiel gegen einen durchschnittlichen Gegner auf neutralem Platz. Ebenfalls mit den Daten aus der abgelaufenen Bundesliga-Saison hätte man für den VfL Wolfsburg eine mittlere Tordifferenz von 1 und für Borussia Dortmund von 0,15 geschätzt. Um zu einer Spielprognose zu kommen, muss man nach Heuer noch die mittlere Anzahl der Tore pro Spiel berücksichtigen. Für diese beiden Mannschaften wäre das 2,92 und Heuer würde für den VfL Wolfsburg 1,885 Tore und für Borussia Dortmund 1,035 Tore schätzen. Für Saisonprognosen berücksichtigt Heuer in seinem kompletten Modell noch weitere Parameter wie die Heimstärke, den Marktwert oder das Abschneiden der Mannschaften in den Vorsaisons. Das Endspiel endete in der Praxis dann mit 3 Toren für Wolfsburg und einem Tor für Dortmund.
2/3-Gesetz beim Roulette
Die Poisson-Verteilung ergibt eine gute Schätzung, wie viele verschiedene Nummern bei 37 Roulette-Spielen getroffen werden.


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 13.11. 2025