Poisson-Prozess
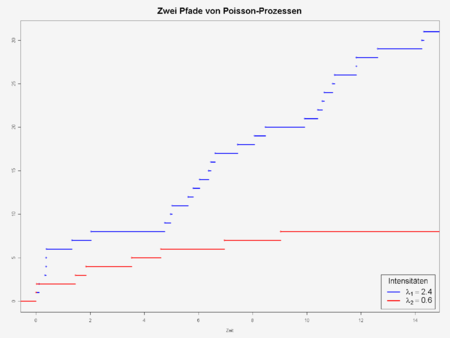
Ein Poisson-Prozess ist ein nach Siméon Denis Poisson benannter stochastischer Prozess. Er ist ein Erneuerungsprozess, dessen Zuwächse Poisson-verteilt sind.
Die mit einem Poisson-Prozess beschriebenen seltenen Ereignisse besitzen aber typischerweise ein großes Risiko (als Produkt aus Kosten und Wahrscheinlichkeit). Daher werden damit oft im Versicherungswesen zum Beispiel Störfälle an komplexen Industrieanlagen, Flutkatastrophen, Flugzeugabstürze usw. modelliert.
Parameter
Die Verteilung der Zuwächse hat einen Parameter λ, dieser wird als Intensität des Prozesses bezeichnet, da pro Zeiteinheit genau λ Sprünge erwartet werden (Erwartungswert der Poisson-Verteilung ist ebenfalls λ). Die Höhe jedes Sprunges ist eins, die Zeiten zwischen den Sprüngen sind exponentialverteilt. Der Poisson-Prozess ist also ein diskreter Prozess in stetiger (d.h. kontinuierlicher) Zeit.
Definition
Ein Poisson-Punktprozess
ist ein zufälliges
Maß, genauer gesagt ein Punktprozess,
mit einem s-endlichen
Intensitätsmaß
auf einem beliebigen Maßraum
,
der folgende beiden Bedingungen erfüllt:
- Für jede messbare Menge
ist die Zufallsvariable
Poisson-verteilt mit Parameter
. Das heißt, es gilt
für alle
.
- Für jede beliebige Anzahl an paarweise disjunkten Mengen
sind die Zufallsvariablen
unabhängig.
Für einen Poisson-Punktprozess wird auch die Kurzschreibweise
verwendet. Handelt es sich um einen homogenen (d.h. auch
stationären) Poisson Punktprozess, so schreibt man auch
,
wobei damit das
-fache
Lebesgue-Maß gemeint
ist. Für das Intensitätsmaß gilt
.
Poisson-Punktprozesse können auf beliebigen Räumen betrachtet werden. Häufig
interessiert man sich für den Raum
oder für die positive reelle Achse
.
Insbesondere wenn man von einem Poisson-Punktprozess auf der reellen Achse
spricht, nennt man die zweite Eigenschaft auch unabhängige Inkremente.
Die Terminologie ist leider nicht einheitlich. Manche Autoren sprechen vom
Poisson-Prozess und meinen damit den Poisson-Punktprozess, andere
wiederum meinen mit Poisson-Prozess den Poisson-Zählprozess,
also .
Letzteres zählt die Anzahl der Punkte des Poisson-Punktprozesses bis zum
Zeitpunkt
.
Definition auf 
Ein stochastischer
Prozess mit càdlàg-Pfaden
über einem Wahrscheinlichkeitsraum
heißt (homogener) Poisson-Prozess
mit Intensität
und
,
falls folgende drei Bedingungen erfüllt sind:
(Siehe Fast sichere Eigenschaften).
. Dabei bezeichnet
die Poisson-Verteilung mit Parameter
.
- Sei für
eine Folge
gegeben. Dann ist die Familie
von Zufallsvariablen stochastisch unabhängig.
Für die Definition des inhomogenen Poisson-Prozesses siehe Inhomogener Poisson-Prozess.
Eigenschaften
- Ein Poisson-Prozess ist gemäß Definition ein stochastischer Prozess mit unabhängigen Zuwächsen.
- Ein homogener Poisson-Prozess ist ein Markow-Prozess
in stetiger Zeit mit diskretem Zustandsraum. Die Q-Matrix ist
.
- Der Zeitraum zwischen zwei Zuwächsen, also
ist exponentialverteilt mit dem Parameter
. Die Wartezeit auf den nächsten Sprung ist also gedächtnislos, d.h. die Restwartezeit auf den nächsten Sprung ist unabhängig von der bisherigen Wartezeit. Daraus folgt, dass auch hier das Wartezeitparadoxon gilt.
- Demnach ist die Wartezeit bis zum
-ten Sprung
gammaverteilt mit Parametern
und
. Man sieht das deutlich, wenn man
als
schreibt.
- Ist
ein Poisson-Prozess und
, so ist
für
wieder ein Poisson-Prozess, d.h. die Zuwächse homogener Poisson-Prozesse sind stationär. Ein homogener Poisson-Prozess ist also ein spezieller Lévy-Prozess.
- Für den Erwartungswert
und die Varianz
gilt
.
- Für die quadratische
Variation gilt
, da der stetige Martingalanteil
verschwindet und alle Sprünge die Höhe 1 haben.
- Da der Pfad des Prozesses monoton steigt, ist
ein Submartingal bezüglich seiner natürlichen Filtrierung.
- Falls man einen stochastischen Prozess hat, der die drei definierenden Eigenschaften erfüllt, so existiert eine Version des Prozesses mit càdlàg-Pfaden, also ein Poisson-Prozess.
heißt kompensierter Poisson-Prozess und ist ein Martingal bezüglich seiner natürlichen Filtrierung.
- Unter relativ allgemeinen Annahmen konvergiert die Überlagerung von allgemeinen Erneuerungsprozessen asymptotisch gegen einen Poisson-Prozess (Satz von Palm-Chintschin).
- Es gilt der Abbildungsatz, das heißt ein Poisson-Punktprozess mit
Intensität
in einer messbaren Abbildung
, bildet wieder einen Poisson-Punktprozess mit der Intensität
ist.
Alternative Definition
In der obigen Definition wird die Poisson-Verteilung vorausgesetzt, sie lässt sich aber auch aus grundlegenden Eigenschaften eines stochastischen Prozesses (Poissonsche Annahmen) ableiten. Wenn diese Eigenschaften einem Geschehen in guter Näherung zugeordnet werden können, wird die Ereignishäufigkeit Poisson-verteilt sein. Poisson veröffentlichte 1837 seine Gedanken zu dieser Verteilung zusammen mit seiner Wahrscheinlichkeitstheorie in dem Werk „Recherches sur la probabilité des jugements en matières criminelles et en matière civile“ („Untersuchungen zur Wahrscheinlichkeit von Urteilen in Straf- und Zivilsachen“).
Man betrachtet ein Raum- oder Zeitkontinuum ,
in dem zählbare Ereignisse mit konstanter mittlerer Anzahl
pro Einheitsintervall
stattfinden (ein Bernoulli-Experiment
wird sehr oft, sozusagen an jedem Punkt des Kontinuums durchgeführt). Nun
richtet man den Blick auf ein genügend kleines Kontinuumsintervall
,
das je nach Experiment einen Bereich, ein Zeitintervall, eine abgegrenzte
Strecke, Fläche oder Volumen darstellen kann. Was sich dort ereignet, bestimmt
die globale Verteilung auf dem Kontinuum.
Die drei Poissonschen Annahmen lauten:
- Innerhalb des Intervalls
gibt es höchstens ein Ereignis (Seltenheit).
- Die Wahrscheinlichkeit, ein Ereignis im Intervall zu finden, ist
proportional zur Länge des Intervalls
. Da
konstant ist, ist es damit auch unabhängig von
.
- Das Eintreten eines Ereignisses im Intervall
wird nicht beeinflusst von Ereignissen, die in der Vorgeschichte stattgefunden haben (Geschichtslosigkeit).
Mit Annahme 1 und 2 ist die Wahrscheinlichkeit, ein Ereignis im Intervall
zu finden, gegeben als
sowie die Wahrscheinlichkeit eines leeren Intervalls durch
Nach Annahme 3 ist die Wahrscheinlichkeit eines leeren Intervalls
unabhängig vom Auftreten irgendwelcher Ereignisse im Bereich
davor. So berechnet man die Wahrscheinlichkeit für kein Ereignis bis zum Punkt
zu
Das ergibt näherungsweise die gewöhnliche
Differentialgleichung
mit der Lösung
unter der Anfangsbedingung
.
Ebenso findet man die Wahrscheinlichkeit für
Ereignisse bis zum Punkt
Jedes angehängte Intervall
darf nach Annahme 1 nur entweder kein oder ein Ereignis enthalten. Die
entsprechende Differentialgleichung
hat die Lösung
Identifiziert man nun in diesem Ausdruck, der die Wahrscheinlichkeit des
Eintretens von
Ereignissen im Kontinuumsbereich
beschreibt, die Parameter
mit
und
mit
,
stimmt er mit der Formel der Poisson-Verteilung überein. Die Zahl
ergibt sich in vielen Aufgabenstellungen als Produkt einer Rate (Anzahl
von Ereignissen pro Einheitsintervall) und einem Vielfachen des
Einheitsintervalls.
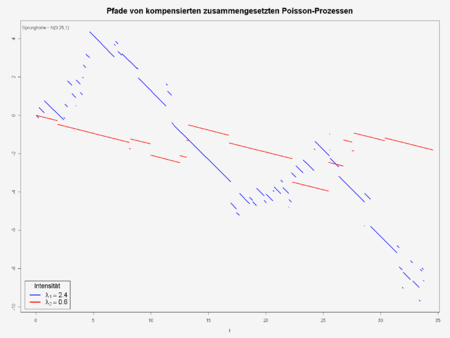
Zusammengesetzte Poisson-Prozesse
Ist
ein Poisson-Prozess mit Intensität
sowie
unabhängig
und identisch verteilte Zufallsvariablen unabhängig von
,
so wird der stochastische Prozess
als zusammengesetzter Poisson-Prozess bezeichnet.
ist dann zusammengesetzt
Poisson-Verteilt. Wie der ursprüngliche Poisson-Prozess ist auch X
ein Sprungprozess
unabhängiger Zuwächse und exponential(µ)-verteilter Abstände zwischen den
Sprüngen, mit Sprunghöhen, die nach Y verteilt sind. Gilt
f.s., so erhält man wieder einen Poisson-Prozess.
Für den Erwartungswert gilt die Formel von Wald (nach dem Mathematiker Abraham Wald),
.
Für die Varianz gilt die Blackwell-Girshick-Gleichung:
.
Zusammengesetzte Poisson-Prozesse sind Lévy-Prozesse.
Inhomogener Poisson-Prozess
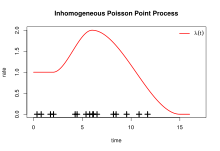
In manchen Fällen kann es sinnvoll sein,
nicht als Konstante, sondern als Funktion
der Zeit aufzufassen.
muss dabei die beiden Bedingungen
für alle
und
für
erfüllen.
Für einen inhomogenen Poisson-Prozess
gilt abweichend von einem homogenen Poisson-Prozess:
, wobei
wieder die Poisson-Verteilung mit dem Parameter
bezeichnet.
- Für den Erwartungswert gilt
.
- Für die Varianz
gilt ebenfalls
.
- Sind
und
zwei Sprungstellen des inhomogenen Poisson-Prozesses, dann ist
exponentialverteilt mit dem Parameter 1.
Cox-Prozess
Ein inhomogener Poisson-Prozess mit stochastischer Intensitätsfunktion
heißt doppelt stochastischer Poisson-Prozess oder nach dem englischen
Mathematiker David
Cox auch Cox-Prozess. Betrachtet man eine bestimmte Realisierung von
,
verhält sich ein Cox-Prozess wie ein inhomogener Poisson-Prozess. Für den
Erwartungswert von
gilt
-
.
Anwendungsbeispiele
- Allgemein:
- Zählung von gleichverteilten Ereignissen pro Flächen-, Raum- oder Zeitmaß (z.B. Anzahl der Regentropfen auf einer Straße; Anzahl der Sterne in einem Volumen V ist ein dreidimensionaler Poisson-Prozess)
- Bestimmung der Häufigkeit seltener Ereignisse wie Versicherungsfälle, Zerfallsprozesse, Reparaturaufträge oder der Zahl der Tore in einem Fußballspiel
- Bediensysteme:
- die zufällige Anzahl von Telefonanrufen pro Zeiteinheit
- die zufällige Anzahl der Kunden an einem Schalter pro Zeiteinheit
- die Zeitpunkte, in denen Anforderungen (Personen, Jobs, Telefonanrufe, Heap, …) bei einem Bediener (Bank, Server, Telefonzentrale, Speicherverwaltung, …) eingehen
- Fehler, Ausfälle, Qualitätskontrolle:
- die zufällige Anzahl von nichtkeimenden Samenkörnern aus einer Packung
- die Orte, an denen ein Faden Noppen hat
- Anzahl der Pixelfehler auf einem LCD
- Anzahl der Schlaglöcher auf einer Landstraße
- Anzahl der Druckfehler in einem Buch
- Anzahl der Unfälle pro Zeiteinheit an einer Kreuzung
- Physik:
- die Zeitpunkte, in denen eine radioaktive Substanz ein
-Teilchen emittiert
- zufällige Anzahl der
-Teilchen, die von einer radioaktiven Substanz in einem bestimmten Zeitraum emittiert werden
- die Zeitpunkte, in denen eine radioaktive Substanz ein
- Versicherungsmathematik:
- die Zeitpunkte von Großschäden einer Versicherung. In der Finanz- und Schadensversicherungsmathematik wird das Auftreten von zu deckenden Schäden üblicherweise durch einen zusammengesetzten Poisson-Prozess beschrieben, bei dem die einzelnen, unabhängig voneinander auftretenden Schäden nach Y verteilt sind. Versieht man diesen Schadensprozess dann noch mit einem deterministischen, negativen Drift (Versicherungsbeiträge), so erhält man den Vermögensprozess des Versicherungsunternehmens, auch Risikoprozess genannt. Dem schließen sich Fragestellungen an wie: Wie wahrscheinlich ist es, dass der Vermögensprozess einen gewissen Schwellwert x, das heißt die Rücklagen der Versicherung, überschreitet und damit einen Konkurs erleidet (sogenanntes Ruin-Problem)? Wie stark muss der negative Drift beziehungsweise der Beitragssatz sein, um die Wahrscheinlichkeit eines Konkurses (sog. Ruinwahrscheinlichkeit) unter eine vorgegebene Schwelle zu drücken?
- Finanzmathematik:
- Modelle für Kurse von Aktien, wobei auch Sprünge erlaubt sind. Hierfür werden zwar oft Lévy-Prozesse verwendet, aber da unendliche Aktivität oft schwer zu messen ist, werden auch zusammengesetzte Poissonprozesse verwendet.
- Kreditrisikomodelle helfen CDS, -Spreads und andere Kreditderivate zu bewerten und modellieren.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.05. 2021