
Martingal
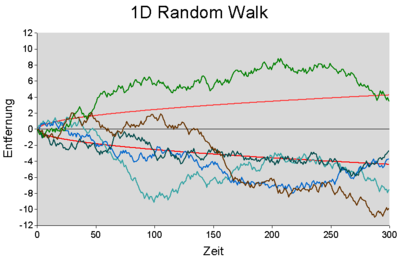
Als Martingal bezeichnet man in der Wahrscheinlichkeitstheorie einen stochastischen Prozess, der über den bedingten Erwartungswert definiert wird und sich dadurch auszeichnet, dass er im Mittel fair ist. Martingale entstehen auf natürliche Weise aus der Modellierung von fairen Glücksspielen. Sie wurden von Paul Lévy in die Mathematik eingeführt.
Eng verwandt mit den Martingalen sind die Supermartingale, dies sind stochastische Prozesse, bei denen im Mittel ein Verlust auftritt, und Submartingale, dies sind stochastische Prozesse, bei denen im Mittel ein Gewinn auftritt.
Definition
Diskreter Fall
Gegeben seien ein Wahrscheinlichkeitsraum
sowie eine Filtrierung
.
Gegeben sei ein stochastischer
Prozess
auf
,
für den gilt:
- Der Prozess ist ein integrierbarer
Prozess, das heißt, es ist
für alle
.
- Der Prozess ist adaptiert
an
, das heißt,
ist
-messbar für alle
.
Dann heißt
ein Martingal (bezüglich
),
wenn
gilt.
Dabei bezeichnet
den bedingten
Erwartungswert der Zufallsvariablen
,
gegeben die σ-Algebra
.
Allgemeiner Fall
Sind ein Wahrscheinlichkeitsraum
sowie eine beliebige, geordnete
Indexmenge
(meist
)
und eine Filtrierung
gegeben, so heißt ein integrierbarer, an
adaptierter Prozess
ein Martingal (bezüglich
),
wenn für alle
gilt
.
Supermartingale und Submartingale
Ein integrierbarer und an
adaptierter diskreter stochastischer Prozess heißt Submartingal, wenn
,
und Supermartingal, wenn
gilt. Im stetigen Falle definiert man analog ein Submartingal über
.
und ein Supermartingal über
.
Submartingale sind also im Gegensatz zu Martingalen tendenziell steigend, Supermartingale tendenziell fallend.
Bemerkung
Die Eigenschaft, ein (Sub-/Super-)Martingal zu sein, kommt nicht
stochastischen Prozessen allein zu, sondern immer einem stochastischen Prozess
in Kombination mit einer Filtrierung. Daher sollte die Filtrierung immer mit
angegeben werden. Manche Autoren geben keine Filtrierung mit an, wenn sie die
von dem Prozess selbst erzeugte
Filtrierung verwenden, die durch
gegeben ist. Wenn
ein Martingal bezüglich einer Filtrierung
ist, dann ist es auch ein Martingal bezüglich
.
Motivierendes Beispiel
Der Begriff des Martingals lässt sich als Formalisierung und
Verallgemeinerung eines fairen Glücksspiels
auffassen. Sei dazu
das Startkapital des Spielers. Dieses wird in vielen Fällen eine Konstante sein,
aber auch ein zufälliges Startkapital ist denkbar. Der zufällige Gewinn im
ersten Spiel werde mit
bezeichnet. Er kann positiv, null oder negativ (also ein Verlust) sein. Das
Kapital des Spielers nach dem ersten Spiel beträgt
und allgemein nach dem
-ten
Spiel
wenn
den Gewinn im
-ten
Spiel bezeichnet. Bei einem fairen Glücksspiel ist der Erwartungswert jedes
Gewinns gleich null, d.h., es gilt
für alle
.
Der Spielverlauf werde nun bis zum Zeitpunkt
einschließlich beobachtet, d.h. die Kapitalstände
seien bekannt. Falls nun der Gewinn im nächsten, also im
-ten,
Spiel unabhängig vom bisherigen Spielverlauf ist, dann berechnet sich das
erwartete Gesamtkapital
nach dem nächsten Spiel unter Berücksichtigung aller zur Verfügung stehenden
Informationen mit Hilfe der Rechenregeln für bedingte Erwartungswerte als
Damit ist gezeigt, dass sich das Kapital eines Spielers, der an einem fairen Glücksspiel teilnimmt, als Martingal modellieren lässt.
Bei realen Glücksspielen, wie beispielsweise beim Roulette,
ist jedoch wegen des Bankvorteils
der erwartete Gewinn bei jedem Spiel im Allgemeinen negativ, also .
Dann ergibt sich analog zur obigen Rechnung
Aus Sicht des Spielers handelt es sich in diesem Fall um ein Supermartingal (Merkspruch: „Supermartingale sind super für die Spielbank“).
Beispiele
Von einer Filtrierung erzeugtes Martingal
Ist
ein Wahrscheinlichkeitsraum,
eine Filtration und
eine
-integrierbare
Zufallsvariable auf
.
Dann wird durch
ein Martingal (bezüglich )
definiert.
Um zu zeigen, dass es sich um ein Martingal handelt, rechnet man die Definition nach:
.
Somit handelt es sich um ein Martingal. Dabei ist die erste Umformung das Einsetzen der Definition, die zweite eine Anwendung der Turmregel des bedingten Erwartungswertes und die dritte wieder Einsetzen der Definition.
Doob-Martingal
Ein Spezialfall des obigen Martingals sind Doob-Martingale:
Ist eine P-integrierbare Zufallsvariable
gegeben und wird die Filtrierung durch eine Folge von Zufallsvariablen
erzeugt, also
,
so heißt das Martingal, welches durch
definiert wird, ein Doob-Martingal (benannt nach Joseph L. Doob).
Beispiele für zeitstetige Martingale
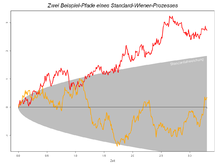
- Ein Wiener-Prozess
ist ein Martingal, ebenso sind für einen Wiener-Prozess
die Prozesse
und die geometrische brownsche Bewegung ohne Drift
Martingale.
- Ein Poisson-Prozess
mit Rate
, der um seine Drift bereinigt wird, also
, ist ein Martingal.
- Nach dem Lemma von Itō gilt: Jedes Itō-Integral (mit beschränktem Integranden) ist ein Martingal. Nach dem Itoschen Martingaldarstellungssatz lässt sich umgekehrt jedes Martingal (sogar jedes lokale Martingal) bezüglich einer von einer Brownschen Bewegung erzeugten Filtration als Ito-Integral bezüglich ebendieser Brown'schen Bewegung darstellen.
- Jedes stetige Martingal ist entweder von unendlicher Variation oder konstant.
- Jedes gestoppte Martingal ist wieder ein Martingal.
Eigenschaften
Rechenregeln
ist genau dann ein Submartingal, wenn
ein Supermartingal ist
- Sind
(Sub-)Supermartingale und ist
, dann ist auch
ein (Sub-)Supermartingal.
- Sind
Martingale, so ist auch
ein Martingal für
.
- Sind
Supermartingale, dann ist auch
-
- ein Supermartingal.
- Sind
Submartingale, dann ist auch
-
- ein Submartingal.
- Ist
eine konvexe Funktion und
ein Martingal und gilt
, so ist
ein Submartingal.
Einfluss der Filtrierung
Sind zwei Filtrierungen
gegeben und ist
kleiner als
in dem Sinne, dass für jedes
gilt
,
so ist jedes
-Martingal
auch ein
-Martingal.
Quadratische Variation und Exponentialmartingal
Ist die quadratische
Variation
eines stetigen beschränkten Martingals
(oder eines mit endlichen exponentiellen Momenten) endlich, so ist der
stochastische Prozess
ebenfalls ein Martingal.
Ebenso ist das sogenannte Exponentialmartingal
von ,
gegeben durch
- >
ein Martingal. Dies folgt aus dem Kazamaki-Kriterium.
Wichtige Aussagen über Martingale
Ungleichungen
Die wichtigsten Ungleichungen im Bezug auf Martingale sind die Doobsche Maximalungleichung und die Aufkreuzungsungleichung. Die Doobsche Maximalungleichung liefert eine Abschätzung dafür, welcher Maximalwert eines Martingals bis zu einem gegebenen Zeitpunkt nicht überschritten wird. Die Aufkreuzungsungleichung liefert eine Aussage darüber, wie oft ein Submartingal ein vorgegebenes Intervall von unten nach oben durchquert.
Kombination mit Stoppzeiten
Das Optional Stopping Theorem und das Optional Sampling Theorem kombinieren Stoppzeiten mit Martingalen und beschäftigen sich mit den Eigenschaften und Erwartungswerten der gestoppten Prozesse. Mit diesen Ergebnissen kann man zeigen, dass keine Abbruchstrategie für ein faires Spiel existiert, die für den Spieler vorteilhaft ist.
Martingaltransformation
Ein Martingal und ein vorhersagbarer, lokal beschränkter Prozess lassen sich mittels des diskreten stochastischen Integrals zu einem neuen Martingal kombinieren. Man nennt diesen Prozess dann die Martingaltransformierte des ursprünglichen Martingals. Die Martingaltransformierte ist wieder ein Martingal. Dies hat weitreichende Folgen für die Existenz von Spielstrategien in fairen Spielen, die dem Spieler im Mittel Gewinn bringen. Modelliert das Martingal das faire Spiel und der vorhersagbare, lokal beschränkte Prozess die Spielstrategie, so folgert aus der Martingaltransformation, dass es keine Spielstrategie gibt, die dem Spieler im Allgemeinen einen Vorteil bringt.
Doob-Zerlegung
Die Doob-Zerlegung erlaubt für jeden adaptierten integrierbaren stochastischen Prozess eine Zerlegung in ein Martingal und einen vorhersagbaren Prozess.
Martingalkonvergenzsatz
Der Martingalkonvergenzsatz liefert für Zufallsvariablen, die ein Martingal bilden, Kriterien unter denen sie fast sicher oder im p-ten Mittel konvergieren.
Abgeleitete Prozessklassen
Lokale Martingale
Lokale Martingale sind Prozesse, für die eine monoton wachsende Folge von Stoppzeiten existiert, so dass für jede Stoppzeit der gestoppte Prozess ein Martingal ist.
Semimartingale
Semimartingale sind eine Klasse von adaptierten Prozessen mit Càdlàg-Pfaden (Die Pfade sind rechtsseitig stetig und die linksseitigen Limites existieren), die sich in ein lokales Martingal, ein Prozess mit lokal endlicher Variation und einen fast sicher endlichen Anteil zerlegen lassen.
Rückwärtsmartingale
Rückwärtsmartingale sind Martingale, bei denen die Indexmenge umgekehrt wird. Sie laufen quasi "falschherum" bzw. von hinten nach vorne.
Herkunft des Wortes
Die Martingale ist eine seit dem 18. Jahrhundert bekannte Strategie im Glücksspiel, bei der nach einem verlorenen Spiel der Einsatz erhöht, im einfachsten Fall verdoppelt wird, so dass im hypothetischen Falle unerschöpflichen Vermögens, unerschöpflicher Zeit, und der Nichtexistenz eines Höchsteinsatzes sicherer Gewinn einträte.
Da die Martingale das bekannteste Spielsystem war und ist, wurde der Begriff auch als Synonym für „Spielsystem“ gebraucht und fand so Eingang in die mathematische Literatur.
Das Wort „Martingale“ selbst stammt aus dem Provenzalischen und leitet sich von der französischen Stadt Martigues im Département Bouches-du-Rhône am Rande der Camargue ab, deren Einwohner früher als etwas naiv galten. Der provenzalische Ausdruck jouga a la martegalo bedeutet so viel wie sehr waghalsig zu spielen.
Der „Martingal“ genannte Hilfszügel soll ebenfalls nach der Stadt Martigues benannt sein, hierbei handelt es sich um einen optionalen Teil der Pferdeausrüstung, der das Pferd daran hindern soll, den Kopf nach oben zu reißen und zu steigen. Dass dieser Hilfszügel ebenfalls Martingal genannt wird, war den Pionieren der Martingaltheorie nicht bekannt – und hat mit der mathematischen Begriffsbildung nichts zu tun.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.11. 2021