Càdlàg-Funktion
Eine Càdlàg-Funktion (auch Cadlag) ist eine spezielle reellwertige Funktion, die beispielsweise in der Stochastik angewendet wird. Dabei ist Càdlàg ein französisches Akronym (französisch continue à droite, limite à gauche „rechtsseitig stetig, mit Grenzwerten von links“). Teils findet sich auch die aus dem englischen abgeleitete RCLL (right continuous, left limits). Analog spricht man auch von Càglàd-Funktionen (oder Làdcàg-Funktionen) (continue à gauche, limite à droite).
Definition
Sei
ein polnischer
Raum wie beispielsweise
.
Eine Funktion
heißt
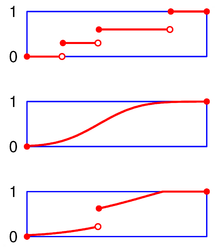
- Càdlàg-Funktion, wenn für alle
die Funktion
in
rechtsseitig stetig ist und der linksseitige Grenzwert in
existiert und endlich ist.
- Càglàd-Funktion, wenn für alle
die Funktion
in
linksseitig stetig ist und der rechtsseitige Grenzwert in
existiert und endlich ist.
Der Raum
aller Càdlàg-Funktionen
auf einem Intervall
,
wird oft mit
bezeichnet.
Anwendungen in der Stochastik
Die Verteilungsfunktion
einer reellen Zufallsvariablen
ist stets eine Càdlàg-Funktion.
Ein stochastischer Prozess
wird càdlàg genannt, wenn fast
sicher jeder Pfad
an jeder Stelle
rechtsseitig stetig ist und dort die linksseitigen Grenzwerte existieren. Ein
Beispiel dafür sind Poisson-Prozesse.
Literatur
- Achim Klenke: Wahrscheinlichkeitstheorie. 3. Auflage. Springer-Verlag, Berlin/Heidelberg 2013, ISBN 978-3-642-36017-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.03. 2021