Random Walk

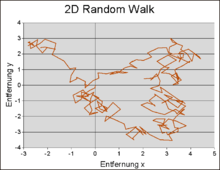
Simulation eines 2D-Random-Walk mit 229 Schritten und einer zufälligen Schrittweite aus dem Intervall [−0,5;0,5] für x- und y-Richtung

Ein Random Walk (deutsch zufällige (stochastische) Irrfahrt, zufällige Schrittfolge, Zufallsbewegung, Zufallsweg) ist ein mathematisches Modell für eine Bewegung, bei der die einzelnen Schritte zufällig erfolgen. Es handelt sich um einen stochastischen Prozess in diskreter Zeit mit unabhängigen und identisch verteilten Zuwächsen. Random-Walk-Modelle eignen sich für nichtdeterministische Zeitreihen, wie sie beispielsweise in der Finanzmathematik zur Modellierung von Aktienkursen verwendet werden (Random-Walk-Theorie). Mit ihrer Hilfe können auch die Wahrscheinlichkeitsverteilungen von Messwerten physikalischer Größen verstanden werden. Der Begriff geht zurück auf Karl Pearsons Aufsatz The Problem of the Random Walk aus dem Jahr 1905.

Definition

Sei $(Z_{1},Z_{2},\dotsc )$ eine Folge von unabhängigen Zufallsvariablen mit Werten in $\mathbb {R} ^{d}$ , die alle die gleiche Verteilung besitzen. Dann heißt der durch

$X_{n}=X_{0}+\sum _{{j=1}}^{n}Z_{j},\qquad n\in \mathbb{N} _{0}$

definierte stochastische Prozess $(X_{n})_{{n\in \mathbb{N} _{0}}}$ ein Random Walk in $\mathbb {R} ^{d}$ oder ein d-dimensionaler Random Walk. Häufig wird $X_{0}=0\in \mathbb{R} ^{d}$ gewählt. Ein Random Walk ist also ein diskreter Prozess mit unabhängigen und stationären Zuwächsen.

Eindimensionaler Fall

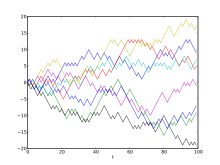
Übergangsgraph des eindimensionalen symmetrischen Random Walk

Acht Realisierungen eines einfachen eindimensionalen Random Walks mit Start in 0. Die Grafik zeigt die aktuelle Position in Abhängigkeit von der Nummer des Schrittes.

Der einfache eindimensionale Random Walk ist ein grundlegendes Einführungsbeispiel, das auf mehrere Dimensionen erweitert und verallgemeinert werden kann; er hat aber bereits selbst zahlreiche konkrete Anwendungen. Beim eindimensionalen Random Walk bilden die einzelnen Schritte einen Bernoulli-Prozess, das heißt, eine Folge von unabhängigen Bernoulli-Versuchen.

Eine beliebte Veranschaulichung lautet wie folgt: Ein desorientierter Fußgänger läuft in einer Gasse mit einer Wahrscheinlichkeit einen Schritt nach vorne und mit einer Wahrscheinlichkeit q=1-p einen Schritt zurück. Seine zufällige Position nach Schritten wird mit $X_{n}$ bezeichnet, ohne Einschränkung sei seine Startposition bei $0$ . Wie groß ist die Wahrscheinlichkeit $P(X_{n}=x)$ , dass er sich genau im n-ten Schritt an der Stelle befindet? Antwort: Der Fußgänger hat insgesamt n=k+l Schritte gemacht, davon Schritte nach vorne und Schritte zurück. Seine Position nach Schritten ist also $X_{n}=k-l=k-(n-k)=2k-n$ und die Wahrscheinlichkeit dafür lautet

$P(X_{n}=2k-n)={n \choose k}~p^{k}q^{{n-k}}$ ,

denn die Anzahl der Schritte nach vorne folgt einer Binomialverteilung.

Oft interessiert man sich speziell für den ungerichteten oder symmetrischen Random Walk mit $p=q={\tfrac {1}{2}}$ . Dies ist auch die einzige Parameterwahl, die zu einer rekurrenten Markow-Kette führt, das heißt, dass der Läufer unendlich oft zum Ursprung zurückkehrt. Die aufsummierten Zufallsvariablen sind dann alle Rademacher-verteilt. Des Weiteren ist die Wahrscheinlichkeitsverteilung der zurückgelegten Strecke symmetrisch um x=0 , und auch der Erwartungswert ist $E(X_{n})=0$ . Das Vorankommen des Fußgängers kann man dann nur durch den mittleren quadratischen Abstand vom Ausgangspunkt, also durch die Varianz der Binomialverteilung beschreiben: $E(X_{n}^{2})=n$ . Das ist ein wichtiges Ergebnis, mit dem eine charakteristische Eigenschaft von Diffusionsprozessen und Brown’scher Molekularbewegung wiedergefunden wird: Das mittlere Quadrat des Abstands eines diffundierenden Teilchens von seinem Ausgangsort wächst proportional zur Zeit.

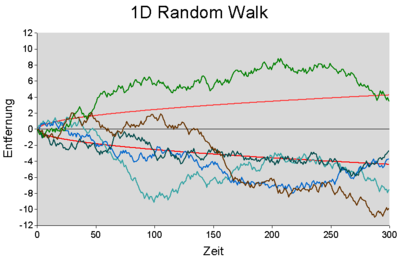
Simulation mehrerer 1D-Random-Walks

Eine erste Verallgemeinerung besteht darin, dass bei jedem Schritt eine zufällige Schrittlänge zugelassen ist. Die nebenstehende Abbildung zeigt beispielsweise fünf Simulationen für n=300 Schritte mit einer Schrittlänge, die im Intervall [-0{,}5;0{,}5] gleichverteilt ist. In diesem Fall beträgt die Standardabweichung für jeden Schritt $\sigma ={\tfrac {1}{{\sqrt {12}}}}=0{,}28868$ . Die Standardabweichung einer derartigen Zufallsbewegung mit Schritten beträgt dann ${\tfrac {{\sqrt {n}}}{{\sqrt {12}}}}$ Einheiten. Sie ist als rote Linie für positive und negative Entfernungen eingezeichnet. Um diese Strecke wird sich der Fußgänger im Mittel fortbewegen. Die relative Abweichung ${\sqrt {n}}/n$ geht gegen null, die absolute Abweichung $\sqrt{n}$ wächst hingegen unbeschränkt.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de