Markow-Kette

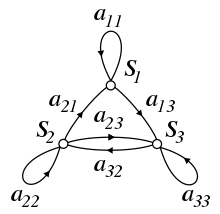
Markow-Kette mit drei Zuständen und unvollständigen Verbindungen

Eine Markow-Kette (englisch Markov chain; auch Markow-Prozess, nach Andrei Andrejewitsch Markow; andere Schreibweisen Markov-Kette, Markoff-Kette, Markof-Kette) ist ein spezieller stochastischer Prozess. Eine Markow-Kette ist darüber definiert, dass auch durch Kenntnis einer nur begrenzten Vorgeschichte ebenso gute Prognosen über die zukünftige Entwicklung möglich sind wie bei Kenntnis der gesamten Vorgeschichte des Prozesses.

Man unterscheidet Markow-Ketten unterschiedlicher Ordnung. Im Falle einer Markow-Kette erster Ordnung heißt das: Der zukünftige Zustand des Prozesses ist nur durch den aktuellen Zustand bedingt und wird nicht durch vergangene Zustände beeinflusst. Die mathematische Formulierung im Falle einer endlichen Zustandsmenge benötigt lediglich den Begriff der diskreten Verteilung sowie der bedingten Wahrscheinlichkeit, während im zeitstetigen Falle die Konzepte der Filtration sowie der bedingten Erwartung benötigt werden.

Ziel bei der Anwendung von Markow-Ketten ist es, Wahrscheinlichkeiten für das Eintreten zukünftiger Ereignisse anzugeben.

Die Begriffe Markow-Kette und Markow-Prozess werden im Allgemeinen synonym verwendet. Zum Teil sind aber zur Abgrenzung mit Markow-Ketten Prozesse in diskreter Zeit (diskreter Zustandsraum) gemeint und mit Markow-Prozessen Prozesse in stetiger Zeit (stetiger Zustandsraum).

Einführende Beispiele

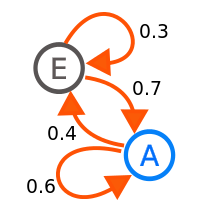
Numerisches Beispiel einer einfachen Markow-Kette mit den zwei Zuständen E und A.

Markow-Ketten eignen sich sehr gut, um zufällige Zustandsänderungen eines Systems zu modellieren, falls man Grund zu der Annahme hat, dass die Zustandsänderungen nur über einen begrenzten Zeitraum hinweg Einfluss aufeinander haben oder sogar gedächtnislos sind. Ein Beispiel sind Auslastungen von Bediensystemen mit gedächtnislosen Ankunfts- und Bedienzeiten.

Diskrete, endliche Markow-Kette

Ein populäres Beispiel für eine zeitdiskrete Markow-Kette mit endlichem Zustandsraum ist die zufällige Irrfahrt (engl. Random Walk) auf einem diskreten Kreis, modelliert durch den Restklassenring ${\mathbb Z}/n{\mathbb Z}$ . Dies führt zum endlichen Zustandsraum $S=\left\{0,1,2,\dots ,(n-1)\right\}$ . Hierbei startet man in der Äquivalenzklasse [0] der 0, und bewegt sich in jedem Schritt aus dem aktuellen Zustand [i] jeweils mit Wahrscheinlichkeit 1/2 nach [i+1] oder nach [i-1] (also anschaulich: einen Schritt nach links oder nach rechts).

Eine (endliche) zufällige Irrfahrt mit zwei absorbierenden Zuständen (ganz links und ganz rechts). Die Zustände „-1“, „0“ und „1“ haben jeweils die gleiche Übergangswahrscheinlichkeit (0,5) zu den Zuständen links und rechts von ihnen.

Diskrete, unendliche Markow-Kette

Als Beispiel für einen abzählbar unendlichen Zustandsraum wirft man eine Münze immer wieder und notiert bei jedem Wurf, wie oft bislang ‚Kopf‘ erschienen ist. Die Abfolge der so gebildeten Zahlen bildet eine (zeitdiskrete) Markow-Kette, diesmal mit Zustandsraum $S=\{0,1,2,\dots \}$ mit jeweils der Übergangswahrscheinlichkeit 1/2 für den Übergang von [i] nach [i+1] und für das Verbleiben in [i] .

Ein weiteres Beispiel für eine Markow-Kette mit unendlichem Zustandsraum ist der Galton-Watson-Prozess, der oftmals zur Modellierung von Populationen genutzt wird.

Diskrete Zeit und höchstens abzählbar unendliche Zustandsmenge

Definition

Gegeben sei eine Familie von Zufallsvariablen $Y=(X_{t})_{{t\in {\mathbb {N}}}}$ , wobei alle $X_{t}$ nur Werte aus dem höchstens abzählbaren Zustandsraum $S=\{s_{1},s_{2},s_{3},\dots \}$ annehmen. Dann heißt eine (diskrete) Markow-Kette genau dann, wenn

${\begin{aligned}&\ P(X_{{t+1}}=s_{{j_{{t+1}}}}\mid X_{t}=s_{{j_{t}}},X_{{t-1}}=s_{{j_{{t-1}}}},\dots ,X_{0}=s_{{j_{0}}})\\=&\ P(X_{{t+1}}=s_{{j_{{t+1}}}}\mid X_{t}=s_{{j_{{t}}}}).\end{aligned}}$

gilt. Die Übergangswahrscheinlichkeiten hängen also nur von dem aktuellen Zustand ab und nicht von der gesamten Vergangenheit. Dies bezeichnet man als Markow-Eigenschaft oder auch als Gedächtnislosigkeit. Seien

$p_{{ij}}(t):=P(X_{{t+1}}=s_{j}\mid X_{t}=s_{i}),\quad i,j=1,\dots ,m$

die Übergangswahrscheinlichkeiten. Diese lassen sich dann in eine quadratische Übergangsmatrix zusammenfassen:

${\mathbf {M}}(t)=(p_{{ij}}(t))_{{s_{i},s_{j}\in S}}$

Sind die Übergangswahrscheinlichkeiten unabhängig vom Zeitpunkt , gilt also $p_{{ij}}(t)=p_{{ij}}$ für alle , so heißt die Markow-Kette homogen oder Kette mit stationären Übergangswahrscheinlichkeiten. Bei Homogenität einer Kette definiert man $p_{ij}^{n}=P(X_{n}=s_{j}\mid X_{0}=s_{i})$ als die n-Schritt-Übergangswahrscheinlichkeit.

Markow-Kette n-ter Ordnung

Gelegentlich werden auch Markow-Ketten n-ter Ordnung untersucht. Bei diesen hängt der zukünftige Zustand von den vorherigen Zuständen ab:

${\begin{aligned}&\ P(X_{{t+1}}=s_{{j_{{t+1}}}}\mid X_{t}=s_{{j_{t}}},X_{{t-1}}=s_{{j_{{t-1}}}},\dots ,X_{0}=s_{{j_{0}}})\\=&\ P(X_{{t+1}}=s_{{j_{{t+1}}}}\mid X_{t}=s_{{j_{t}}},\dots ,X_{{t-n+1}}=s_{{j_{{t-n+1}}}}).\end{aligned}}$

In diesem Sinn sind die oben betrachteten Markow-Ketten Ketten erster Ordnung. Ketten höherer Ordnung werden hier aber nicht weiter betrachtet.

Grundlegende Eigenschaften

Die Verteilung von wird manchmal auch als Startverteilung oder Anfangsverteilung bezeichnet. Bei Vorgabe einer Startverteilung sind alle weiteren Verteilungen $X_{t}$ eindeutig bestimmt. Daher hat sich teilweise die verkürzte Notation eingebürgert, nur die Startverteilung $\alpha$ und den Zeitschritt von Interesse anzugeben:

$P^{\alpha }(X_{t}=i):=P(X_{t}=i|X_{0}\ {\text{ hat Verteilung }}\ \alpha )$

Startet man in einem eindeutigen Zustand

, so wird meist $P^{j}(X_{t}=i)$ geschrieben.

Bei einem endlichen Zustandsraum lassen sich Markow-Ketten mittels der Übergangsmatrix und von Wahrscheinlichkeitsvektoren beschreiben. Wählt man einen stochastischen Startvektor $v_{0}$ (als Zeilenvektor) als Startverteilung, so ergibt sich die Verteilung zum Zeitpunkt 1 durch $v_{1}=v_{0}M$ . Damit folgt induktiv $v_{n}=v_{0}M^{n}$ . Dabei ist dann genau der -te Eintrag von $v_{n}$ die Wahrscheinlichkeit zum Zeitpunkt im Zustand zu sein, wenn mit der Startverteilung $v_{0}$ gestartet wurde.
Gemäß der obigen Ausführung lassen sich im Falle der Homogenität und der Endlichkeit des Zustandsraumes leicht die -Schritt-Übergangswahrscheinlichkeiten berechnen. Diese sind dann genau

$p_{ij}^{n}=\left[M^{n}\right]_{i,j}$ ,

also der Eintrag, der in der

-ten Zeile und der

-ten Spalte der -ten Potenz der Übergangsmatrix steht.

Allgemein gilt die Chapman-Kolmogorow-Gleichung. Im Falle eines endlichen Zustandsraumes ist sie genau das komponentenweise Ausschreiben der Matrixmultiplikation.
Markow-Ketten sind diskrete dynamische Systeme. Der Zeitraum ist $\mathbb{N}$ , der Index der Zufallsvariable. Den Zustandsraum im Sinne des dynamischen Systems bilden dann alle Verteilungen auf dem Zustandsraum im Sinne der Markow-Kette. Die Operation $\Phi$ ordnet dann der Verteilung im -ten Zeitschritt die Verteilung im -ten Zeitschritt zu. Im Falle eines endlichen Zustandsraumes der Markow-Kette ist dies dann genau die iterierte Anwendung der Übergangsmatrix wie oben beschrieben. Einige Begriffe aus der Theorie der dynamischen Systeme haben ein Pendant in der Theorie der Markow-Ketten wie z.B. kritische Punkte und stationäre Verteilungen.
Homogene Markow-Ketten mit einer stationären Verteilung als Startverteilung sind stark stationäre stochastische Prozesse. Somit sind zeitdiskrete Markow-Ketten mit abzählbarem Zustandsraum maßerhaltende dynamische Systeme, wenn sie in ihrer invarianten Verteilung starten. Sind sie zusätzlich positiv rekurrent sowie irreduzibel, so sind sie sogar ergodische stochastische Prozesse und erlauben die Anwendung von Aussagen der Ergodentheorie wie zum Beispiel des individuellen Ergodensatzes.
Die oben definierte Übergangsmatrix ist unendlichdimensional, wenn der Zustandsraum abzählbar unendlich ist. Nur im Falle der Endlichkeit des Zustandsraumes handelt es sich um eine Matrix im Sinne der Linearen Algebra.

Beispiele

Endlicher Zustandsraum

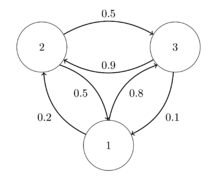
Übergangsgraph für die beschriebene Markow-Kette

Wir versuchen, mithilfe einer Markow-Kette eine einfache Wettervorhersage zu bilden. Dazu kodieren wir 1 = „die Sonne scheint“, 2 = „es ist bewölkt“ und 3 = „es regnet“. Als Zeitschritt wählen wir einen Tag. Aus Erfahrung wissen wir, dass wenn heute die Sonne scheint, die Wahrscheinlichkeit, dass es morgen regnet, ungefähr 80 % ist und die Wahrscheinlichkeit, dass es bewölkt ist, ca. 20 % beträgt. Außerdem treffen wir die Annahme, dass sich diese Wahrscheinlichkeiten nicht ändern, die Markow-Kette also homogen ist. Somit wissen wir nun

$P(X_{t+1}=i|X_{t}=1)={\begin{cases}0&{\text{ falls }}\quad i=1\\0{,}2&{\text{ falls }}\quad i=2,\\0{,}8&{\text{ falls }}\quad i=3\end{cases}}$

Ist es aber bewölkt, so regnet es mit Wahrscheinlichkeit 0,5 am folgenden Tag und mit Wahrscheinlichkeit von 0,5 scheint die Sonne. Es gilt also

$P(X_{t+1}=i|X_{t}=2)={\begin{cases}0{,}5&{\text{ falls }}\quad i=1\\0&{\text{ falls }}\quad i=2,\\0{,}5&{\text{ falls }}\quad i=3\end{cases}}$

Regnet es heute, so scheint danach nur mit Wahrscheinlichkeit von 0,1 die Sonne und mit Wahrscheinlichkeit von 0,9 ist es bewölkt. Damit folgt für die Übergangswahrscheinlichkeiten

$P(X_{t+1}=i|X_{t}=3)={\begin{cases}0{,}1&{\text{ falls }}\quad i=1\\0{,}9&{\text{ falls }}\quad i=2,\\0&{\text{ falls }}\quad i=3\end{cases}}$

Damit ist die Markow-Kette vollständig beschrieben. Anschaulich lassen sich solche Markow-Ketten gut durch Übergangsgraphen darstellen, wie oben abgebildet. Ordnet man nun die Übergangswahrscheinlichkeiten zu einer Übergangsmatrix an, so erhält man

$M = \begin{bmatrix} 0 & 0{,}2 & 0{,}8 \\ 0 {,}5 & 0 & 0{,}5 \\ 0{,}1 & 0{,}9 & 0 \end{bmatrix}$

Wir wollen nun wissen, wie sich das Wetter entwickeln wird, wenn heute die Sonne scheint. Dazu geben wir die Anfangsverteilung X_0 vor in Form des stochastischen Startvektors $v_{0}=(1;0;0)$ . Wir starten also fast sicher im Zustand 1. Multiplikation von rechts mit der Übergangsmatrix liefert $v_{1}=v_{0}M=(0;0{,}2;0{,}8)$ . Mit achtzigprozentiger Wahrscheinlichkeit regnet es also. Am dritten Tag gilt $v_{3}=v_{0}M^{3}\approx (0{,}3700;0{,}1260;0{,}5040)$ . Somit ist die Regenwahrscheinlichkeit am dritten Tag knapp über 50 % und die Sonnenwahrscheinlichkeit knapp unter 40 %. Somit lässt sich für jedes vorgegebene Wetter am Starttag die Regen- und Sonnenwahrscheinlichkeit an einem beliebigen Tag angeben. Auch Fragestellungen wie: „Heute scheint die Sonne. Wie groß ist die Wahrscheinlichkeit, dass es vor drei Tagen geregnet hat?“ lassen sich mit dem Satz von Bayes beantworten.

Abzählbar unendlicher Zustandsraum

Definieren wir nun eine Markow-Kette auf dem Zustandsraum $\mathbb {Z}$ und mit Übergangswahrscheinlichkeiten

$P(X_{t+1}=i|X_{t}=j)={\begin{cases}p&{\text{ falls }}\quad i=j+1\\q&{\text{ falls }}\quad i=j-1,\\0&{\text{sonst}}\end{cases}}$

wobei $p+q=1,p,q\geq 0$ gilt. Dies lässt sich so veranschaulichen: Startet man an einem beliebigen Punkt, so bewegt man sich entweder mit einer Wahrscheinlichkeit von nach „rechts“, sprich begibt sich zu der nächsthöheren Zahl. Mit Wahrscheinlichkeit wandert man nach „links“ zu einer niedrigeren Zahl. Entsprechend diesem Vorgehen irrt man dann über den Zahlenstrahl. Daher wird diese Markow-Kette auch Irrfahrt auf $\mathbb {Z}$ genannt. Gelegentlich wird für solche Markow-Ketten auch der Begriff des Random Walk verwendet. Starten wir im Zustand 0, so ist mit den obigen Übergangswahrscheinlichkeiten

$P^{0}(X_{1}=i)={\begin{cases}p&{\text{ falls }}\quad i=1\\q&{\text{ falls }}\quad i=-1,\\0&{\text{ sonst}}\end{cases}}$

Daraus folgt dann $P^{0}(X_{2}=-2)=q^{2},P^{0}(X_{2}=0)=2pq,P^{0}(X_{2}=2)=p^{2}$ . Hier zeigt sich ein gewisser Zusammenhang zur Binomialverteilung. Außerdem gilt aber auch $P^{0}(X_{2}=-1)=P^{0}(X_{2}=1)=0$ . Gewisse Zustände können also nur zu bestimmten Zeiten besucht werden, eine Eigenschaft, die Periodizität genannt wird.

Ist allgemeiner $(Z_{n})_{n\in \mathbb {N} }$ eine Folge unabhängiger und identisch verteilter Zufallsvariablen mit Werten in $\mathbb {Z}$ , dann ist durch

$X_{t}=\sum _{n=1}^{t}Z_{n}$

eine Markow-Kette $(X_{t})_{t\in \mathbb {N} }$ mit Übergangswahrscheinlichkeiten $p_{ij}=P(Z_{1}=j-i)$ gegeben.

Klassische Beispiele

Einige der bekanntesten Markow-Ketten sind

Die Irrfahrt auf ${\mathbb {Z}}^{D}$ sowie Verallgemeinerungen auf Graphen.
Der Galton-Watson-Prozess, welcher die Fortpflanzung einer sich eingeschlechtlich fortpflanzenden Spezies modelliert
Das Ehrenfest-Modell zur Modellierung der Diffusion von Molekülen durch Membrane.

Attribute

Markow-Ketten können gewisse Attribute zukommen, welche insbesondere das Langzeitverhalten beeinflussen. Dazu gehören beispielsweise die folgenden:

Irreduzibilität

→ Hauptartikel: Irreduzible Markow-Kette

Irreduzibilität ist wichtig für die Konvergenz gegen einen stationären Zustand. Vereinfacht gesagt ist eine Markow-Kette irreduzibel, wenn für alle Zustände und gilt, dass die Wahrscheinlichkeit, in endlicher Zeit von nach zu kommen, echt positiv ist. Gilt dies für fixierte und , so sagt man auch, dass und miteinander kommunizieren.

Periodizität

→ Hauptartikel: Periodische Markow-Kette

Periodische Markow-Ketten erhalten trotz aller Zufälligkeit des Systems gewisse deterministische Strukturen. Ist eine Markow-Kette periodisch mit Periode , so kann sie höchstens alle Zeitschritte wieder zu ihrem Startpunkt zurückkehren (dies ist aber nicht zwingend).

Rekurrenz und Transienz

→ Hauptartikel: Rekurrente Markow-Kette

Die Rekurrenz und die Transienz beschreiben das Langzeitverhalten einer Markow-Kette. Wird ein Zustand fast sicher unendlich oft besucht, so heißt er rekurrent, ansonsten transient. Sind alle Zustände rekurrent (transient), so heißt die Markow-Kette rekurrent (transient). Wichtiges Hilfsmittel zur Bestimmung von Rekurrenz ist die Green-Funktion.

Absorbierende Zustände

→ Hauptartikel: Absorbierender Zustand

Absorbierende Zustände sind Zustände, welche nach dem Betreten nicht wieder verlassen werden können. Hier interessiert man sich insbesondere für die Absorptionswahrscheinlichkeit, also die Wahrscheinlichkeit, einen solchen Zustand zu betreten.

Stationäre Verteilungen

→ Hauptartikel: Stationäre Verteilung

In der Anwendung sind oftmals besonders stationäre Verteilungen interessant. Gibt man diese Verteilungen als Startverteilung von X_0 vor, so sind alle darauf folgenden Verteilungen der Zustände $X_{n}$ für beliebiges gleich der Startverteilung. Interessant ist hier die Frage, wann solche Verteilungen existieren und wann eine beliebige Verteilung gegen solch eine stationäre Verteilung konvergiert.

Reversibilität

Bei reversiblen Markow-Ketten lässt sich nicht unterscheiden, ob sie in der Zeit vorwärts oder rückwärts laufen, sie sind also invariant unter Zeitumkehr. Insbesondere folgt aus Reversibilität die Existenz eines Stationären Zustandes.

Modellierung

Oft hat man in Anwendungen eine Modellierung vorliegen, in welcher die Zustandsänderungen der Markow-Kette durch eine Folge von zu zufälligen Zeiten stattfindenden Ereignissen bestimmt wird (man denke an obiges Beispiel von Bediensystemen mit zufälligen Ankunfts- und Bedienzeiten). Hier muss bei der Modellierung entschieden werden, wie das gleichzeitige Auftreten von Ereignissen (Ankunft vs. Erledigung) behandelt wird. Meist entscheidet man sich dafür, künstlich eine Abfolge der gleichzeitigen Ereignisse einzuführen. Üblicherweise unterscheidet man dabei zwischen den Möglichkeiten Arrival First und Departure First.

Arrival First (AF)

Bei dieser Disziplin wird zu Beginn eines Zeitschrittes das Bedienen gestartet. Danach treffen neue Forderungen ein, und erst am Ende eines Zeitschrittes tritt das Bedien-Ende auf.

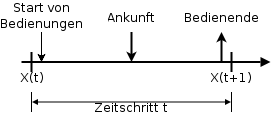
Der Vorteil dieser Disziplin ist, dass Forderungsankünfte immer vor einem möglichen Bedien-Ende eintreffen und damit die PASTA-Eigenschaft (Poisson Arrivals See Time Averages) gilt. Mit Hilfe dieser Eigenschaft lassen sich für Ankünfte, die als Bernoulli-Prozess modelliert sind, unter anderem sehr einfach für Bediensysteme wichtige Eigenschaften wie die Verlustwahrscheinlichkeit $P_{V}$ berechnen.

Als Nachteil kann eine Forderung, die im Zeitschlitz $z_{t}$ eintrifft, frühestens in $z_{{t+1}}$ fertig bedient werden. Dies führt unter Umständen zu einer höheren Anzahl von benötigten Warteplätzen im modellierten System.

Departure First (DF)

Im Fall von Departure First kommen zu Beginn eines Zeitschrittes Forderungen im System an. Darauf folgt der Start von Bedienzeiten und am Ende eines Zeitschrittes das Ende von Bedienzeiten.

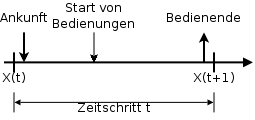
Bei diesem Ansatz gilt die PASTA Eigenschaft nicht mehr, was im Allgemeinen zu komplizierteren Berechnungen als im Falle von Arrival First führt. Eine Forderung kann im selben Zeitschritt eintreffen und fertig bedient werden.

Simulation

Diskrete Markow-Ketten mit endlichem Zustandsraum $S=\{1,\dots ,m\}$ können leicht simuliert werden, wenn Standardzufallszahlen $u_{t}$ verfügbar sind. Dazu definiert man $r_{i}(j)={\begin{cases}0&{\text{falls }}\quad j=0\\\sum _{l=1}^{j}p_{il}&{\text{sonst}}\end{cases}}$

für alle $i,j\in S$ . Ist nun $X_{t}=i$ , dann setze $X_{t+1}=j$ genau dann, wenn $u_{t}\in [r_{i}(j-1),r_{i}(j)]$ ist. Dieses Verfahren ist insbesondere dann effizient, wenn wenige $p_{{ij}}$ ungleich null sind. Es entspricht der Inversionsmethode mit der Wahrscheinlichkeitsfunktion $p_{i}(\{j\}):=p_{{ij}}$ . Die Möglichkeit, auch große Markow-Ketten zu simulieren, macht man sich beim MCMC-Verfahren zunutze, um Verteilungen zu simulieren, die nicht durch klassische Verfahren simuliert werden können.

Stetige Zeit und diskreter Zustandsraum

Analog lässt sich die Markow-Kette auch für kontinuierliche Zeit und diskreten Zustandsraum bilden. Das heißt, dass sich zu bestimmten Zeitpunkten der Zustand sprunghaft ändert.

Sei $(X(t))_{{t\geq 0}}$ ein stochastischer Prozess mit kontinuierlicher Zeit und diskretem Zustandsraum. Dann gilt bei einem homogenen Markow-Prozess

$\forall n\in \mathbb{N} ,\ 0<t_{1}<\dotsb <t_{n},\ t>0,\ i_{1},\ldots ,i_{n},j\in S:$

${\begin{aligned}P(X(t_{n}+t)=j\mid X(t_{n})=i_{n},\ldots ,X(t_{1})=i_{1})&=P(X(t_{n}+t)=j\mid X(t_{n})=i_{n})\\&=P(X(t)=j\mid X(0)=i_{n})\\&=:p_{{i_{n},j}}(t)\end{aligned}}$

Auch hier lassen sich Übergangsmatrizen bilden: $P(t):=[p_{{i,j}}(t)]$ für alle t>0 und P(0):=I (Hierbei steht wie üblich für die Einheitsmatrix).

Es gilt die Chapman-Kolmogorow-Gleichung und $(P(t))_{{t\geq 0}}$ ist entsprechend eine Halbgruppe, die unter gewissen Voraussetzungen einen infinitesimalen Erzeuger, nämlich die Q-Matrix hat.

Beispiel hierfür ist der homogene Poisson-Prozess, der die Q-Matrix $p_{{ij}}=\lambda {\mathbf {1}}_{{\{j=i+1\}}}-\lambda {\mathbf {1}}_{{\{j=i\}}}$ besitzt, oder allgemeiner jeder Geburts- und Todesprozess.

Diskrete Zeit und allgemeiner Zustandsraum

Markow-Ketten können auch auf allgemeinen messbaren Zustandsräumen definiert werden. Ist der Zustandsraum nicht abzählbar, so benötigt man hierzu den stochastischen Kern als Verallgemeinerung zur Übergangsmatrix. Dabei ist eine Markow-Kette durch die Startverteilung auf dem Zustandsraum und den stochastischen Kern (auch Übergangskern oder Markowkern) schon eindeutig bestimmt.

Auf dem Gebiet der allgemeinen Markow-Ketten gibt es noch viele offene Probleme. Gut erforscht sind lediglich Harris-Ketten. Ein klassisches Beispiel für einen Markow-Prozess in stetiger Zeit und stetigem Zustandsraum ist der Wiener-Prozess, die mathematische Modellierung der brownschen Bewegung.

Allgemeine Formulierung

Inhomogene Markow-Prozesse lassen sich mithilfe der elementaren Markow-Eigenschaft definieren, homogene Markow-Prozesse mittels der schwachen Markow-Eigenschaft für Prozesse mit stetiger Zeit und mit Werten in beliebigen Räumen definieren. Meist beschränkt man sich hierbei aber aus Gründen der Handhabbarkeit auf polnische Räume. Eine Verschärfung der schwachen Markow-Eigenschaft ist die starke Markow-Eigenschaft.

Definition

Gegeben sei ein stochastischer Prozess $X=(X_t)_{t \in T}$ , für den gilt:

Für die Indexmenge gilt $T \subset [0,\infty)$ sowie $0 \in T$ und sie ist abgeschlossen bezüglich Addition.
Jedes $X_{t}$ nimmt Werte in $(E, \mathcal B(E))$ an, demnach nimmt Werte in $(E^{\times T}, \mathcal B (E)^{ \otimes T})$ an. Dabei ist $\mathcal B (E)$ die Borelsche σ-Algebra.

Der Prozess heißt dann ein Markow-Prozess mit Verteilungen $(P_x)_{x \in E}$ auf $(\Omega ,{\mathcal A})$ , wenn gilt:

Für alle $x \in E$ ist ein stochastischer Prozess auf $(\Omega, \mathcal A, P_x)$ mit
Es existiert ein Markow-Kern $\kappa$ von $(E, \mathcal B(E))$ nach $(E^{ \times T}, \mathcal B (E)^{\otimes T})$ mit

$\kappa(x, B)= P_x(X \in B)$ für alle $B \in \mathcal B (E)^{ \otimes T}$ .
Es gilt die schwache Markow-Eigenschaft.

Anwendungen

Markow-Ketten werden in unterschiedlichen Bereichen verwendet.

In den Wirtschaftswissenschaften bei der Warteschlangentheorie. Hier unterstellt man eine homogene Markow-Kette. Dort wird die zu einer Periode wartende Anzahl an Kunden betrachtet. Die Wahrscheinlichkeiten für Ankunft oder Abfertigung eines Kunden sind zeitinvariant (unabhängig von der Periode).
Bioinformatik: Markow-Ketten werden in der Bioinformatik dazu verwendet, Sequenzabschnitte auf bestimmte Eigenschaften zu untersuchen. Hierzu zählt z.B. das Vorhandensein von CpG-Inseln, da in diesen die Übergangswahrscheinlichkeiten zwischen C-G und G-C erhöht sind.
In der Gesundheitsökonomie zur probabilistischen Modellierung im Zuge einer Kosten-Nutzen-Analyse von Gesundheitstechnologien wie zum Beispiel Medikamenten.
In der Versicherungsmathematik werden diskrete Markow-Ketten verwendet zur Einrechnung biometrischer Risiken (Invalidisierungswahrscheinlichkeiten, Sterbewahrscheinlichkeiten, …).
Die Finanzmathematik verwendet auf dem Wiener-Prozess basierende Markow-Prozesse zur Modellierung von Aktienkurs- und Zinsentwicklungen.
In der Musik zur Komposition algorithmischer Werke, zum Beispiel bei Iannis Xenakis.
Im Qualitätsmanagement zur Bestimmung der Zuverlässigkeit eines Systems und dessen Teilkomponenten
In der Physik zur Modellierung des Zerfalls eines Compoundkerns und zur Herleitung von Master-Gleichungen in der Markow-Näherung
Im automatisierten Onlinemarketing zur Generierung von Texten, welche von automatischen Spamfiltern nur schwer von durch Menschen verfasste Texte zu unterscheiden sind.
Ebenso zum Erkennen von Spam-Mails mittels eines Markow-Spamfilters
Bestimmte Brettspiele wie Monopoly und das Leiterspiel lassen sich als Markow-Kette auffassen.
Der PageRank einer Homepage lässt sich als Markow-Kette interpretieren. Insbesondere ist diese Markow-Kette durch die stochastische Google-Matrix beschrieben.
Zur Simulation von Verteilungen, die ansonsten nur schwer zugänglich sind, mittels der Markow chain Monte Carlo-Methode

Siehe auch

Endlicher Automat

Basierend auf einem Artikel in:

Wikipedia.de