Dynamisches System

Ein (deterministisches) dynamisches System ist ein mathematisches Modell eines zeitabhängigen Prozesses, der homogen bezüglich der Zeit ist, also dessen weiterer Verlauf nur vom Anfangszustand, aber nicht von der Wahl des Anfangszeitpunkts abhängt. Der Begriff des dynamischen Systems geht in seiner heutigen Form auf die Mathematiker Henri Poincaré und George David Birkhoff zurück.

Dynamische Systeme finden vielfältige Anwendungen auf Prozesse im Alltag und erlauben Einblicke in viele Bereiche nicht nur der Mathematik (z.B. Zahlentheorie, Stochastik), sondern auch der Physik (z.B. Pendelbewegung, Klimamodelle) oder der theoretischen Biologie (z.B. Räuber-Beute-Modelle).

Man unterscheidet zwischen diskreter und kontinuierlicher Zeitentwicklung. Bei einem zeitdiskreten dynamischen System ändern sich die Zustände in äquidistanten Zeitsprüngen, d.h. in aufeinanderfolgenden, stets gleich großen zeitlichen Abständen, während die Zustandsänderungen eines zeitkontinuierlichen dynamischen Systems in infinitesimal kleinen Zeitschritten stattfinden. Das wichtigste Beschreibungsmittel für zeitkontinuierliche dynamische Systeme sind autonome gewöhnliche Differenzialgleichungen. Ein gemischtes System aus kontinuierlichen und diskreten Teilsystemen mit kontinuierlich-diskreter Dynamik wird auch als hybrid bezeichnet. Beispiele solcher hybrider Dynamiken finden sich in der Verfahrenstechnik (z.B. Dosiervorlage-Systeme).

Wichtige Fragestellungen im Zusammenhang mit dynamischen Systemen betreffen vor allem ihr Langzeitverhalten (zum Beispiel Stabilität, Periodizität, Chaos und Ergodizität), die Systemidentifikation und ihre Regelung.

Einführende Beispiele

Exponentielles Wachstum

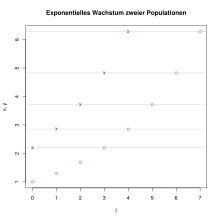
Zwei exponentiell wachsende Populationen x_t (rot) und y_t (blau) mit y₀ = x₃

Ein einfaches Beispiel für ein dynamisches System ist die zeitliche Entwicklung einer Größe, die einem exponentiellen Wachstum unterliegt, wie etwa eine Population einer ungehindert wachsenden Bakterienkultur. Der Zustand zu einem festen Zeitpunkt ist hier durch eine nichtnegative reelle Zahl, nämlich die Bestandsgröße der Population, gegeben, das heißt, der Zustandsraum des Systems ist die Menge $X=[0,\infty )$ der nichtnegativen reellen Zahlen. Betrachtet man zunächst die Zustände $x_{0},x_{1},x_{2},\dotsc$ zu den diskreten Zeitpunkten $t=0,1,2,\dotsc$ , also auf dem Zeitraum $T=\mathbb{N} _{0}$ , dann gilt $x_{{t+1}}=ax_{t}$ mit einem konstanten Wachstumsfaktor . Für den Zustand zu einem Zeitpunkt $t\in T$ ergibt sich daraus $x_{t}=a^{t}x_{0}$ .

Die charakterisierende Eigenschaft eines dynamischen Systems ist, dass der Zustand zwar von der verstrichenen Zeit $t\in T$ und vom Anfangswert $x_{0}\in X$ abhängt, jedoch nicht von der Wahl der Anfangszeitpunkts. Sei etwa $y_{0},y_{1},y_{2},\ldots$ eine weitere exponentiell wachsende Population mit dem gleichen Wachstumsfaktor , aber mit dem Anfangswert $y_{0}=x_{t}$ gegeben. Zu einem Zeitpunkt $s\in T$ gilt dann

$y_{s}=a^{s}y_{0}=a^{s}a^{t}x_{0}=a^{{s+t}}x_{0}=x_{{s+t}}$ .

Die zweite Population wächst also im Zeitabschnitt [0,s] genauso wie die erste im Zeitabschnitt [t,s+t] . Dieses Verhalten lässt sich noch anders ausdrücken: Die sogenannte Flussfunktion $\Phi \colon T\times X\to X$ , die jedem Zeitpunkt $t\in T$ und jedem Anfangszustand $x\in X$ den Zustand $\Phi (t,x)$ zum Zeitpunkt zuordnet, hier also $\Phi (t,x)=a^{t}x$ , erfüllt für alle $s,t\in T$ und alle $x\in X$ die Gleichung

$\Phi {\bigl (}s,\Phi (t,x){\bigr )}=\Phi (s+t,x)$ .

Das ist die sogenannte Halbgruppeneigenschaft des Flusses eines dynamischen Systems.

Federpendel

Eine weitere Quelle für dynamische Systeme ist die mathematische Modellierung mechanischer Systeme, im einfachsten Fall die Bewegung eines Massepunktes unter dem Einfluss einer Kraft, die vom Ort und von der Geschwindigkeit abhängt, aber nicht explizit von der Zeit. Der Zustand eines solchen Systems zu einem Zeitpunkt $t\in T=[0,\infty )$ ist gegeben als das geordnete Paar (x(t),v(t)) , bestehend aus dem Ort x(t) und der Geschwindigkeit v(t) . Insbesondere ist dann der gesamte Bewegungsablauf durch die Vorgabe einer Anfangsposition $x(0)=x_{0}$ zusammen mit einer Anfangsgeschwindigkeit $v(0)=v_{0}$ eindeutig bestimmt. Im Fall einer eindimensionalen Bewegung ist somit der Zustandsraum $X=\mathbb{R} ^{2}$ .

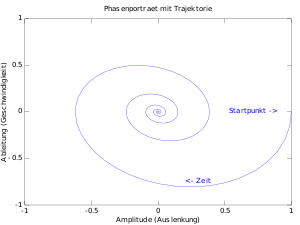Gedämpfte Schwingung und Bahn im Zustandsraum

Als konkretes Beispiel soll ein Federpendel betrachtet werden, auf dessen Massestück mit der Masse die Rückstellkraft der Feder sowie möglicherweise eine geschwindigkeitsabhängige Reibungskraft einwirkt. Bezeichnet man die Gesamtkraft mit F(x(t),v(t)) , so ergibt sich für den Zustand das gewöhnliche Differentialgleichungssystem

${\begin{aligned}{\dot {x}}(t)&=v(t),\\{\dot {v}}(t)&={\frac {1}{m}}F(x(t),v(t)),\end{aligned}}$

wobei der Punkt über den Variablen die Ableitung nach der Zeit bezeichnet. Die erste Gleichung besagt, dass die Geschwindigkeit die Ableitung des Ortes nach der Zeit ist, und die zweite ergibt sich direkt aus dem zweiten newtonschen Axiom, nach dem Masse mal Beschleunigung gleich der auf den Massepunkt wirkenden Gesamtkraft ist.

Es lässt sich zeigen, dass auch bei diesem System der Fluss

$\Phi \colon T\times X\to X,\quad \Phi (t,x_{0},v_{0})={\bigl (}x(t),v(t){\bigr )}$

die Halbgruppeneigenschaft erfüllt. Betrachtet man den Verlauf des Systemzustandes im Zustandsraum $X=\mathbb{R} ^{2}$ , also die sogenannte Bahn $\{(x(t),v(t))\in \mathbb{R} ^{2}\mid t\geq 0\}$ , so ergibt sich bei einer gedämpften Schwingung des Federpendels eine Trajektorie, die spiralförmig auf die Ruhelage (0,0) zuläuft.

Definitionen

Ein dynamisches System ist ein Tripel $(T,X,\Phi ),$ bestehend aus einer Menge $T=\mathbb{N} _{0},\mathbb{Z } ,\mathbb{R} _{0}^{+}$ oder $\mathbb{R} ,$ dem Zeitraum, einer nichtleeren Menge , dem Zustandsraum (dem Phasenraum), und einer Operation $\Phi \colon \,T\times X\to X$ von auf so dass für alle Zustände $x\in X$ und alle Zeitpunkte $t,s\in T$ gilt:

$\Phi (0,x)=x$ (Identitätseigenschaft) und
$\Phi (s,\Phi (t,x))=\Phi (s+t,x)$ (Halbgruppeneigenschaft).

Wenn $T=\mathbb{N} _{0}$ oder $T=\mathbb{Z }$ ist, dann heißt $(T,X,\Phi )$ zeitdiskret oder kurz diskret, und mit $T=\mathbb{R} _{0}^{+}$ oder $T=\mathbb{R}$ nennt man $(T,X,\Phi )$ zeitkontinuierlich oder kontinuierlich. $(T,X,\Phi )$ wird außerdem als diskretes oder kontinuierliches dynamisches System für reelle Zeit oder als invertierbar bezeichnet, falls $T=\mathbb{Z }$ bzw. $T=\mathbb{R}$ gilt.

Für jedes $x\in X$ heißt die Abbildung $\beta _{x}\colon \,T\to X,\,t\mapsto \beta _{x}(t):=\Phi (t,x),$ die Bewegung von $x=\beta _{x}(0)$ und die Menge $O(x):=\{\beta _{x}(t)\mid t\in T\}$ wird die Bahn (der (volle) Orbit, die Trajektorie, die Phasenkurve, die Bahnkurve, die Lösungskurve) von genannt. Der positive Halborbit oder Vorwärtsorbit von ist $O^{+}(x):=\{\beta _{x}(t)\mid t\in T\cap \mathbb{R} _{0}^{+}\}$ und falls $(T,X,\Phi )$ invertierbar ist, ist $O^{-}(x):=\{\beta _{x}(t)\mid -t\in T\cap \mathbb{R} _{0}^{+}\}$ der negative Halborbit oder Rückwärtsorbit von .

Ein diskretes dynamisches System $(T,X,\Phi )$ ist stetig, wenn sein Zustandsraum ein (nichtleerer) metrischer Raum ist und wenn jede zu einem Zeitpunkt $t\in T$ gehörende Transformation $\varphi _{t}\colon \,X\to X,\,x\mapsto \varphi _{t}(x):=\Phi (t,x),$ stetig ist. Man nennt ein kontinuierliches dynamisches System $(T,X,\Phi )$ stetig oder einen Halbfluss, wenn sein Zustandsraum ein metrischer Raum ist und wenn jede zu einem Zeitpunkt gehörende Transformation sowie jede Bewegung eines Zustands stetig ist. Außerdem nennt man ein stetiges diskretes dynamisches System $(\mathbb{Z } ,X,\Phi )$ auch eine Kaskade und einen Halbfluss $(\mathbb{R} ,X,\Phi )$ einen Fluss. Der Zustandsraum eines stetigen dynamischen Systems wird auch als Phasenraum und von jedem $x_{0}\in X$ der Orbit als die Phasenkurve oder Trajektorie von $x_{0}$ bezeichnet, die einfach $x\colon \,t\mapsto x(t)$ geschrieben wird mit $x(0)=x_{0}$ .

Koppelt man kontinuierliche und gegebenen Falles noch zusätzliche diskrete dynamische Systeme zu einem System zusammen, so nennt man dieses ein kontinuierlich-diskretes oder auch hybrides dynamisches System.

Bemerkungen

In der Literatur wird häufig nicht zwischen dynamischen Systemen und stetigen dynamischen Systemen bzw. Flüssen unterschieden, außerdem versteht man unter einem Fluss nicht selten einen differenzierbaren Fluss (siehe unten). Es finden sich auch allgemeinere Definitionen stetiger dynamischer Systeme, bei denen z.B. als Phasenraum eine topologische Mannigfaltigkeit, ein (u.U. kompakter) Hausdorff-Raum oder gar nur ein topologischer Raum genommen wird.
An Stelle der Linksoperation $\Phi$ wie in der obigen Definition werden oft dynamische Systeme mit einer Rechtsoperation $\Phi ^{*}\colon \,X\times T\to X$ auf definiert, die Reihenfolge der Argumente dreht sich dann entsprechend um.
In der Definition wird die Identitätseigenschaft von der Operation $\Phi$ deshalb gefordert, weil jeder Zustand , so lang keine Zeit vergeht (also für ), sich nicht verändern soll. Diese Eigenschaft bedeutet, dass die zu $0$ gehörende Transformation die identische Abbildung auf ist: $\varphi _{0}=\operatorname {id}_{X}.$
Die Halbgruppeneigenschaft macht das dynamische System bezüglich der Zeit homogen: Man gelangt zunächst in Zeiteinheiten vom Zustand zum Zustand $\Phi (t,x)$ und anschließend von dort in Zeiteinheiten zum Zustand $\Phi (s+t,x)$ , d.h. zum gleichen Zustand zu dem man direkt vom Zustand in Zeiteinheiten kommt. Die zu allen Zeitpunkten gehörenden Transformationen $\varphi _{t}\colon \,X\to X,\,x\mapsto \varphi _{t}(x):=\Phi (t,x),$ bilden eine kommutative Halbgruppe mit der Komposition $\circ$ als Verknüpfung und mit einem neutralen Element $\varphi _{0}$ , außerdem ist die Abbildung $T\to X^{X}\!,\,t\mapsto \varphi _{t},$ ein Halbgruppenhomomorphismus: $\varphi _{{s+t}}=\varphi _{{s}}\circ \varphi _{{t}}$ für alle $s,t\in T.$ Diese Transformationshalbgruppe ist bei invertierbaren dynamischen Systemen sogar eine Gruppe, denn für alle $t\in T$ ist $\varphi _{{-t}}$ das inverse Element zu $\varphi _{t}.$
Ein dynamisches System $(T,X,\Phi )$ mit $T=\mathbb{N} _{0}$ oder mit $T=\mathbb{R} _{0}^{+}$ lässt sich genau dann zu einem invertierbaren dynamischen System $(T',X,\Phi ')$ mit $(T'\cap \mathbb{R} _{0}^{+},X,\Phi '|_{{(T'\cap \mathbb{R} _{0}^{+})\times X}})=(T,X,\Phi )$ fortsetzen, wenn die zu gehörende Transformation $\varphi_1$ eine Umkehrfunktion $(\varphi _{1})^{{-1}}$ besitzt. Es sind dann $\varphi _{{-1}}:=(\varphi _{1})^{{-1}}$ und rekursiv $\varphi _{{-(n+1)}}:=\varphi _{{-1}}\circ \varphi _{{-n}}$ für alle $n\in \mathbb{N} .$ Ist $(T,X,\Phi )$ kontinuierlich, so sind durch $\varphi _{{-t}}:=\varphi _{{1-s}}\circ \varphi _{{-(n+1)}}$ für alle $t=n+s\in \mathbb{R} _{0}^{+}$ mit $n \in \N_0$ und $s\in [\,0,1)$ ebenso sämtliche zu negativen Zeiten gehörenden Transformationen eindeutig gegeben. Mit $T':=T\cup \{-t\mid t\in T\}$ ist so genau eine Operation $\Phi '\colon \,T'\times X\to X,\,(t,x)\mapsto \Phi '(t,x):=\varphi _{t}(x),$ von erklärt, so dass $(T',X,\Phi ')$ die invertierbare Fortsetzung von $(T,X,\Phi )$ ist.
Wegen der Halbgruppeneigenschaft lässt sich jedes diskrete dynamische System $(\mathbb{N} _{0},X,\Phi )$ oder $(\mathbb{Z } ,X,\Phi )$ als iterative Anwendung der zu gehörenden Transformation $\varphi :=\varphi _{1}$ mit den Zeitpunkten als Iterationsindizes auffassen: $\varphi _{{t+1}}=\varphi \circ \varphi _{t}$ für alle $t\in \mathbb{N} _{0}$ und bei $(\mathbb{Z } ,X,\Phi )$ ist zusätzlich $\varphi _{{t-1}}=\varphi ^{{-1}}\circ \varphi _{t}$ für alle $-t\in \mathbb{N} _{0}.$ Daher ist $(T,X,\Phi )$ bereits durch $\varphi$ eindeutig bestimmt und lässt sich einfacher $(X,\varphi )$ schreiben.
Schränkt man bei einem kontinuierlichen dynamischen System $(T,X,\Phi ),$ die Zeit auf $T\cap \mathbb{Z }$ ein, dann ergibt sich mit $(T\cap \mathbb{Z } ,X,\Phi |_{{(T\cap \mathbb{Z } )\times X}})$ stets ein diskretes dynamisches System. Diese Diskretisierung findet zum einen in der Numerik eine große Anwendung, wie z.B. bei der Rückwärtsanalyse. Zum anderen existieren natürliche und technische Systeme, die durch nichtkontinuierliche Zustandsänderungen charakterisiert und in direkter Weise durch diskrete Dynamische Systeme modelliert werden können.
Differenzierbare (Halb-)Flüsse sind (Halb-)Flüsse $(T,X,\Phi )$ , bei denen jede zu einem Zeitpunkt gehörende Transformation differenzierbar ist. Insbesondere ist jede dieser Transformationen eines differenzierbaren Flusses ein Diffeomorphismus.
In der Theorie dynamischer Systeme interessiert man sich besonders für das Verhalten von Trajektorien für $t\to \pm \infty$ . Hierbei sind Limesmengen und deren Stabilität von großer Bedeutung. Die einfachsten Limesmengen sind Fixpunkte, das sind diejenigen Punkte $x\in X$ mit $\Phi (t,x)=x$ für alle $t\in T$ , also diejenigen Zustände , deren Bahn die einelementige Menge $\{x\}$ ist. Weiter interessiert man sich für Punkte, deren Bahn für $t\to +\infty$ gegen einen Fixpunkt konvergiert. Die wichtigsten Limesmengen sind neben Fixpunkten die periodischen Orbits. Gerade in nichtlinearen Systemen trifft man aber auch komplexe nichtperiodische Grenzmengen an. In der Theorie der nichtlinearen Systeme werden Fixpunkte, periodische Orbits und allgemeine nichtperiodische Grenzmengen unter dem Oberbegriff Attraktor (bzw. Repeller, falls abstoßend, subsumiert. Diese werden in der Chaostheorie ausführlich untersucht.

Wichtige Spezialfälle

Gewöhnliche Differentialgleichungen

Kontinuierliche dynamische Systeme treten vor allem im Zusammenhang mit gewöhnlichen Differentialgleichungen auf. Gegeben sei die autonome Differentialgleichung

${\dot x}(t)=f(x(t))$

mit einem Vektorfeld $f\colon X\to \mathbb{R} ^{n}$ auf einem Gebiet $X\subseteq \mathbb{R} ^{n}$ . Falls die Gleichung für alle Anfangswerte $x_{0}\in X$ eine für alle $t \in \R$ definierte, eindeutig bestimmte Lösung $\beta _{{x_{0}}}\colon \mathbb{R} \to X$ mit $\beta _{{x_{0}}}(0)=x_{0}$ besitzt, dann ist $(\mathbb{R} ,X,\Phi )$ mit $\Phi (t,x):=\beta _{x}(t)$ ein kontinuierliches dynamisches System. Die Bahnen des Systems sind also die Lösungskurven der Differentialgleichung. Die Fixpunkte sind hier die $x\in X$ mit f(x)=0 ; sie werden auch stationäre oder kritische Punkte des Vektorfeldes genannt.

Iteration

Diskrete dynamische Systeme stehen in enger Beziehung zur Iteration von Funktionen. Ist $g\colon X\to X$ eine Selbstabbildung einer beliebigen Menge , also eine Funktion, die jedem $x\in X$ wieder ein Element $g(x)\in X$ zuordnet, dann kann man zu einem Anfangswert $x_{0}\in X$ die rekursiv definierte Folge $x_{{n+1}}=g(x_{n})$ für $n \in \N_0$ betrachten. Mit der -fachen Hintereinanderausführung $g^{n}=g\circ g\circ \ldots \circ g$ ( Mal) gilt dann $x_{n}=g^{n}(x_{0})$ . Die Gleichung $g^{{m+n}}=g^{m}\circ g^{n}$ zeigt, dass damit $(\mathbb{N} _{0},X,\Phi )$ mit $\Phi (n,x_{0})=g^{n}(x_{0})$ ein diskretes dynamisches System ist. Umgekehrt wird für ein dynamisches System $(\mathbb{N} _{0},X,\Phi )$ durch $g(x):=\Phi (1,x)$ eine Abbildung $g\colon X\to X$ mit $\Phi (n,x_{0})=g^{n}(x_{0})$ definiert. Die Fixpunkte eines solchen Systems sind die $x\in X$ mit g(x)=x .

Beispiel hierfür sind Markow-Ketten in diskreter Zeit mit endlichem Zustandsraum . Der Zustandsraum im Sinne eines dynamischen Systems sind dann alle Wahrscheinlichkeitsvektoren auf , die Zeit ist $T={\mathbb {N}}$ und die Iteration ist gegeben durch die Linksmultiplikation des Wahrscheinlichkeitsvektors $x_{n}$ mit der Übergangsmatrix . Die Fixpunkte sind dann die stationären Verteilungen.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de