Stationäre Verteilung

Eine invariante Verteilung oder stationäre Verteilung ist ein Begriff aus der Theorie der Markow-Ketten; diese wiederum sind spezielle stochastische Prozesse und damit Untersuchungsobjekte der Stochastik. Eine Markow-Kette besitzt eine stationäre Verteilung genau dann, wenn es eine Startverteilung gibt, die sich im Zeitverlauf nicht ändert. Stationäre Verteilungen sind nicht zu verwechseln mit der Stationarität eines stochastischen Prozesses oder stationären Übergangswahrscheinlichkeiten.

Definition

Gegeben sei eine homogene Markow-Kette $(X_{n})_{n\in \mathbb {N} }$ in diskreter Zeit mit höchstens abzählbarem Zustandsraum . Dann heißt eine Verteilung $P_\pi$ auf stationäre Verteilung, wenn

$P_{\pi }(\{j\})=\sum _{i\in Z}P_{\pi }(\{i\})p(i,j)$

für alle $j\in Z$ gilt, wobei $p(i,j)=P(X_{n}=j|X_{{n-1}}=i)$ die Übergangswahrscheinlichkeit von Zustand in den Zustand ist (die unabhängig vom Zeitpunkt ist). Im Falle eines endlichen Zustandsraumes entspricht dies

$\pi M= \pi$ ,

wobei die Übergangsmatrix ist und $\pi$ ein Wahrscheinlichkeitsvektor als Zeilenvektor geschrieben. Damit sind die stationären Verteilungen in diesem Fall genau die Linkseigenvektoren der Übergangsmatrix zum Eigenwert 1, welche bezüglich der Summennorm normiert wurden.

Existenz und Eindeutigkeit

Im Allgemeinen müssen keine stationären Verteilungen existieren. Beispiel hierfür sind transiente Markow-Ketten. Diese besitzen nie stationäre Verteilungen. Umgekehrt lässt sich auch zeigen, dass irreduzible Markow-Ketten höchstens eine stationäre Verteilung besitzen. Für die Eindeutigkeit der stationären Verteilungen gelten folgende Aussagen:

Eine irreduzible Markow-Kette besitzt genau dann eine stationäre Verteilung, wenn sie positiv rekurrent ist. Die Verteilung ist dann gegeben durch

$P_{\pi }(\{i\})={\frac {1}{\operatorname {E}(\tau _{{ii}})}}$ .

Hierbei ist $\tau_{ii}$ die Wiederkehrzeit in den Zustand

, wenn in diesem gestartet wurde.

Im Falle eines endlichen Zustandsraumes sind Irreduzibilität der Markow-Kette und Irreduzibilität der Übergangsmatrix äquivalent. Daraus folgt aber sofort mit dem Satz von Perron-Frobenius, dass eine eindeutige invariante Verteilung (bzw. Linkseigenvektor) existiert und damit dass die Markow-Kette positiv-rekurrent ist. Somit folgt hier aus Irreduzibilität positive Rekurrenz.
Demnach hat eine irreduzible Markow-Kette mit endlichem Zustandsraum immer eine stationäre Verteilung. Diese entspricht genau dem normierten Linkseigenvektor zum Eigenwert 1 der Übergangsmatrix bzw. dem normierten Eigenvektor der transponierten Übergangsmatrix zum Eigenwert 1.
Erfüllt eine Verteilung die Detailed-Balance-Gleichung, so ist diese Verteilung eine stationäre Verteilung.

Konvergenz

Eine irreduzible, positiv rekurrente Markow-Kette konvergiert genau dann gegen eine stationäre Verteilung, wenn sie aperiodisch ist. Konvergenz bedeutet hier, dass

$\lim _{{n\to \infty }}P(X_{n}=i)=P_{\pi }(\{i\})$

für jede Startverteilung von X_0 und jeden Zustand $i \in Z$ gilt.

Ist der Zustandsraum endlich, so konvergieren dann die Zeilen von M^n gegen die stationäre Verteilung.

Bei endlichen Zustandsräumen findet sich oft das Konvergenzkriterium, dass ein $k \in \mathbb{N}$ existieren muss, so dass für die Übergangsmatrix gilt, dass $M^{k}>0$ ist. Dies entspricht der Überprüfung der Matrix auf Aperiodizität und Irreduzibilität.

Verzichtet man auf die Aperiodizität, so lässt sich folgende Aussage zeigen: Ist eine Markow-Kette Irreduzibel und Rekurrent, so ist

$\lim _{{N\to \infty }}{\frac {1}{N}}\sum _{{n=0}}^{{N-1}}P(X_{n}=i)={\frac {1}{\operatorname {E}(\tau _{{ii}})}}=P_{\pi }(\{i\})$ .

Der Mittelwert der Eintrittswahrscheinlichkeiten konvergiert also komponentenweise gegen die stationäre Verteilung.

Allgemeiner gilt: ist die Markow-Kette nicht irreduzibel, so zerfällt sie in mehrere Teilmengen von Zuständen, die miteinander kommunizieren und alle dieselbe Periode besitzen. Ist K(i) solch eine Menge mit einem beliebigen aber fixierten Zustand aus dieser Menge. Dann lässt sich jeder Zustand aus dieser Menge in einer eindeutigen Zahl von Schritten von aus erreichen. Ist die Teilmenge T(i) nun rekurrent, so gilt

$\lim _{{n\to \infty }}p_{{ij}}^{{nd+k}}={\frac {d}{\operatorname {E}(\tau _{{jj}})}}$ .

Konvergenzgeschwindigkeit

Für einige Anwendungen ist vor allem interessant, wie schnell die stationäre Verteilung erreicht wird. Es lässt sich zeigen, dass wenn $1=\lambda _{1}>|\lambda _{2}|\geq |\lambda _{3}|\dots$ für gilt, und alle Eigenwerte einfach sind, die folgende Abschätzung gilt:

$\Vert v_{0}M^{n}-P_{\pi }\Vert \leq C|\lambda _{2}|^{n}$

Für eine beliebige Startverteilung $v_{0}$ . Wichtigster Einflussfaktor auf die Konvergenzgeschwindigkeit ist also der betragsmäßig zweitgrößte Eigenwert.

Es lassen sich noch vergleichbare Aussagen für schwächere Voraussetzungen an die Übergangsmatrix zeigen, dabei müssen aber Korrekturterme für die Jordanblöcke eingeführt werden.

Beispiele

Endlicher Zustandsraum

Existenz

Betrachten wir die Markow-Kette mit der folgenden Übergangsmatrix:

$M= \begin{bmatrix} 1 & 0 & 0 & 0 & 0\\ 0{,}1 & 0 & 0{,}8 & 0{,}1 &0\\ 0 &0{,}5 & 0 & 0 & 0{,}5 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix}$

Diese Markow-Kette hat zwei absorbierende Mengen: $A= \{1\}$ und $B=\{4,5\}$ . Da diese Zustände nicht mehr verlassen werden können, haben sie einen Einfluss auf die Existenz der stationären Verteilungen. Dies zeigt sich auch in den normierten Eigenvektoren. Diese sind $\pi_1=(1,0,0,0,0)$ und $\pi_2=(0,0,0,0{,}5,0{,}5)$ . Somit ist hier die stationäre Verteilung nicht eindeutig.

Eindeutigkeit

Die untersuchte Markow-Kette

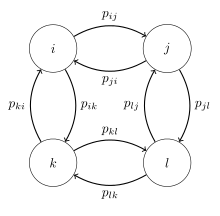
Betrachten wir die Markow-Kette mit dem rechts dargestellten Übergangsgraph. Der Einfachheit halber setzen wir alle Übergangswahrscheinlichkeiten auf 0,5. Die Markow-Kette ist irreduzibel, da man sich von jedem Zustand in maximal zwei Schritten in jeden anderen Zustand bewegen kann. Sie ist aber auch periodisch, da eine Rückkehr zum Startpunkt nur zu geraden Zeitpunkten möglich ist. Die ebenfalls irreduzible Übergangsmatrix ist dann

$M = \begin{bmatrix} 0 & 0{,}5 & 0 & 0{,}5 \\ 0{,}5 & 0 & 0{,}5 & 0 \\ 0 & 0{,}5 & 0 & 0{,}5 \\ 0{,}5 & 0 & 0{,}5 & 0 \end{bmatrix}$

Der Satz von Perron-Frobenius garantiert die Eindeutigkeit des Eigenvektors, da die Matrix zusätzlich doppelt-stochastisch ist, hat sie die stationäre Verteilung $\pi= \frac{1}{4}(1,1,1,1)$ . Die Matrixpotenzen konvergieren aber nicht, insbesondere ist $M^{2n+1} = M$ und

$M^{2n} =M^2 = \begin{bmatrix} 0{,}5 & 0 & 0{,}5 & 0 \\ 0 & 0{,}5 & 0 & 0{,}5 \\ 0{,}5 & 0 & 0{,}5 & 0 \\ 0 & 0{,}5 & 0 & 0{,}5 \end{bmatrix}$

Betrachten wir aber nun die Mittelwerte, so konvergieren diese gegen die entsprechende Komponente der Stationären Verteilung:

$\lim _{{N\to \infty }}{\frac {1}{N}}\sum _{{n=0}}^{{N-1}}P(X_{n}=1|X_{0}=1)=\lim _{{N\to \infty }}{\frac {1}{N}}\sum _{{n=0}}^{{N-1}}p_{{11}}^{n}\rightarrow {\frac {1}{4}}{\text{ für }}N\to \infty$ .

Dies folgt hier mithilfe der entsprechenden Einträge (im Beispiel die erste Zeile und Spalte) der obigen Übergangsmatrix.

Konvergenz

Eine einfache Markow-Kette

Betrachte die rechts dargestellte Markow-Kette mit den Übergangswahrscheinlichkeiten wie in der Übergangsmatrix angegeben:

$M = \begin{bmatrix} 0{,}5 & 0 & 0{,}5 \\ 0 {,}1 & 0{,}5 & 0{,}4 \\ 0 & 0{,}5 & 0{,}5 \end{bmatrix}$

Es gilt dann

$M^2= \frac{1}{100} \begin{bmatrix} 25 & 25 & 50 \\ 10 & 45 & 45 \\ 5 & 50 & 45 \end{bmatrix} >0$

Somit ist die Markow-Kette irreduzibel (und damit auch positiv rekurrent), aperiodisch und konvergiert demnach gegen eine stationäre Verteilung. Ein Eigenvektor von M^T zum Eigenwert 1 ist v=(1,5,5) , Normierung auf 1 bzgl. der Summennorm liefert als eindeutige invariante Verteilung

$\pi=\frac{1}{11} (1,5,5) = (0.0909,0.4545,0.4545)$ .

Berechnet man die Matrixpotenzen, so stimmen bei M^6 schon zwei Nachkommastellen mit der exakten Lösung überein, bei $M^{12}$ schon mehr als vier Nachkommastellen. Umgekehrt kann man aus der als Linkseigenvektor berechneten stationären Verteilung bei Konvergenz sofort den Grenzwert der Matrixpotenzen angeben, da diese Zeilenweise gegen die stationäre Verteilung konvergieren:

$\lim _{{n\to \infty }}M^{n}={\frac {1}{11}}\cdot {\begin{bmatrix}1&5&5\\1&5&5\\1&5&5\end{bmatrix}}$

Aus der stationären Verteilung kann man auch die erwartete Rückkehrzeit berechnen, diese ist genau der Kehrwert der entsprechenden Komponente der Verteilung. Somit ist hier die durchschnittliche Zeit beim Start in 1 bis zur Rückkehr

$\operatorname {E}(\tau _{{11}})={\frac {1}{\pi _{1}}}=11$ .

Variante des Random Walk

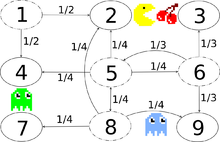
Übergangsgraph mit Übergangswahrscheinlichkeiten exemplarisch für die Zustände 1, 5, 6 und 8. Es gibt einen Geheimgang zwischen den Zuständen 2 und 8 für beide Richtungen.

Die Spielfigur Pac-Man frisst in einem Labyrinth kleine Kugeln und Kirschen und wird dabei von Gespenstern verfolgt. Der Einfachheit halber ist die Spielwelt in diesem Beispiel ein kleines $3\times3$ -Gitter und die Monster bewegen sich rein zufällig. Jedes horizontal und vertikal angrenzende Spielfeld ist mit gleicher Wahrscheinlichkeit der nächste Aufenthaltsort des Gespensts, mit Ausnahme eines Geheimgangs zwischen den Zuständen und (siehe nebenstehenden Übergangsgraphen).

Der Zustandsraum lautet $Z=$ { $1,2,3,4,5,6,7,8,9$ }. In der nun folgenden Übergangsmatrix wurden Einträge mit Wahrscheinlichkeit $0$ entfernt, um eine bessere Übersichtlichkeit zu erhalten:

$P={\begin{pmatrix}&{\frac {1}{2}}&&{\frac {1}{2}}\\{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}&&&{\frac {1}{4}}\\&{\frac {1}{2}}&&&&{\frac {1}{2}}\\{\frac {1}{3}}&&&&{\frac {1}{3}}&&{\frac {1}{3}}\\&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}\\&&{\frac {1}{3}}&&{\frac {1}{3}}&&&&{\frac {1}{3}}\\&&&{\frac {1}{2}}&&&&{\frac {1}{2}}\\&{\frac {1}{4}}&&&{\frac {1}{4}}&&{\frac {1}{4}}&&{\frac {1}{4}}\\&&&&&{\frac {1}{2}}&&{\frac {1}{2}}\end{pmatrix}}$

Diese Markov-Kette ist irreduzibel, da sich die Gespenster in endlicher Zeit von jedem beliebigen Zustand in jeden beliebigen Zustand begeben können. Dank des Geheimgangs sind hierfür nur maximal drei Zustandswechsel nötig. Durch den Geheimgang ist die Markov-Kette auch aperiodisch, weil die Monster sowohl in einer geraden als auch in einer ungeraden Anzahl an Zustandswechseln von jedem beliebigen Zustand in jeden beliebigen Zustand wechseln können. Ohne den Geheimgang wäre die Markov-Kette periodisch, weil dann ein Übergang von einem geraden in einen geraden Zustand bzw. von einem ungeraden in einen ungeraden Zustand nur in einer geraden Anzahl von Zustandswechseln möglich wäre.

Wegen der Irreduzibilität und Aperiodizität gibt es genau eine stabile Gleichgewichtsverteilung, welche die Markov-Kette nach einer unendlich langen Zeit annimmt. Die Aufenthaltswahrscheinlichkeiten für die einzelnen Zustände ändern sich nach langer Zeit (fast) nicht mehr. Die stationäre Verteilung lässt sich naiv bestimmen, indem in die Gleichung

$\pi _{n}=\pi _{0}\cdot P^{n}$

für eine beliebige Startverteilung $\pi _{0}$ ein großes eingesetzt wird, weil die Matrixpotenzen wie im obigen Beispiel konvergieren. Um eine analytische Lösung zu berechnen, ist das lineare Gleichungssystem

$\pi =\pi \cdot P$

nach $\pi$ aufzulösen, unter der Nebenbedingung einer Zeilensumme von . Das Einsetzen der naiven Lösung in diese Gleichung dient als Kontrolle. Die obige Gleichung ist äquivalent zu

$(P^{T}-I)\cdot \pi ^{T}=0$ .

Die Übergangsmatrix wird demnach transponiert und die Einheitsmatrix subtrahiert. Der gesuchte Vektor der Zustandswahrscheinlichkeiten ist nun ein Spaltenvektor. Die Lösung des linearen Gleichungssystems ergibt

$\pi =(7.7,15.4,7.7,11.5,15.4,11.5,7.7,15.4,7.7)$ %.

Die Gespenster halten sich demnach am häufigsten in der Mitte auf, weniger oft am Rand und am seltensten in der Ecke. Eine Ausnahme bilden die Randzustände und , welche aufgrund des Geheimwegs durchschnittlich genauso oft besucht werden wie das zentrale Spielfeld.

Abzählbar unendlicher Zustandsraum

Betrachten wir eine Markow-Kette auf dem Zustandsraum $Z=\mathbb{N}_0$ mit Übergangswahrscheinlichkeiten

$p_{{ij}}={\begin{cases}{\frac {1}{i+1}},&{\text{ falls }}j=i+1,\\1-{\frac {1}{i+1}},&{\text{ falls }}j=0,\\0&{\text{sonst}}.\end{cases}}$

Mit einer gewissen Wahrscheinlichkeit steigt man also zu einer Zahl eins höher auf, falls dies nicht geschieht, startet man wieder am Nullpunkt. Es gilt:

alle Zustände kommunizieren miteinander, da jeder Zustand die 0 erreichen kann und die 0 jeden Zustand erreicht. Demnach ist die Markow-Kette irreduzibel.
die Rückkehrzeiten in die 0 sind $\{2,3,4,\dotsc \}$ und demnach hat die 0 die Periode 1, ist also aperiodisch. Aufgrund der Irreduzibilität ist dann auch die gesamte Markow-kette aperiodisch.
Die erwartete Rückkehrzeit zu 0 ist gegeben durch

$\operatorname {E}(\tau _{{00}})=\sum _{{k=2}}^{\infty }{\frac {k}{(k-1)!}}\cdot (1-{\frac {1}{k}})=e$

Somit ist die 0 positiv rekurrent und aufgrund der Irreduzibilität der Markow-Kette auch die gesamte Kette positiv rekurrent.

Die Kette konvergiert also gegen eine von der Startverteilung unabhängige invariante Verteilung. Da wir bereits wissen, dass $P_{\pi }(\{0\})={\frac {1}{e}}$ , können wir die Definition als Rekursionsgleichung nutzen und folgern, dass $P_{\pi }(\{i\})={\frac {1}{i!e}}$ gilt. Dass die Berechnung der stationären Verteilung direkt möglich ist, ist aber die Ausnahme.

Verwendung

Stationäre Verteilungen haben zahlreiche Anwendungen in der Praxis. Stellt man sich die Markow-Kette als zufällig durch einen Graphen wandernden Punkt vor, so ist die i-te Komponente der stationäre Verteilung genau die relative Wahrscheinlichkeit, ihn im Zustand i anzutreffen. Ein Beispiel hierfür ist des Ehrenfest-Modell. Es modelliert die Diffusion von Molekülen durch eine Membran. Der stationäre Zustand ist dann genau die Konzentration, wenn sich ein Diffusionsgleichgewicht eingestellt hat. Ein anderes Beispiel ist die Berechnung des PageRanks mittels des Zufalls-Surfer-Modells. Hier modelliert die Markow-Kette das Verhalten eines Internetnutzers: Mit einer bestimmten Wahrscheinlichkeit wählt er einen der Links auf der Homepage, auf der er sich befindet, aus, andernfalls wählt er eine andere Homepage per Browser aus. Die stationäre Verteilung ist dann die relative Wahrscheinlichkeit, dass der Zufallssurfer auf eine bestimmte Seite trifft. Dies ist dann ein Maß für die Wichtigkeit dieser Seite und auch der normierte PageRank dieser Seite.

Des Weiteren spielen stationäre Verteilungen eine wichtige Rolle bei Markov Chain Monte Carlo-Verfahren. Sie sind genau die Verteilungen, für die eine Stichprobe erstellt werden soll.

Basierend auf einem Artikel in:

Wikipedia.de