
Übergangsgraph
Übergangsgraphen sind spezielle gerichtete Graphen mit Kantengewichten, die eine Verbindung zwischen Stochastik und Graphentheorie schlagen. Sie eignen sich besonders zur anschaulichen Darstellung von zeitdiskreten homogenen Markow-Ketten.
Definition
Ein gerichteter und kantengewichteter Graph
heißt Übergangsgraph, wenn für jeden Knoten
die Kantengewichte der von
ausgehenden Kanten
größer 0 sind und sich zu 1 aufsummieren:
.
Dabei ist
die Nachfolgermenge
von Knoten
,
also die Menge aller Knoten, die durch von
ausgehende Kanten erreicht werden können.
Äquivalent dazu ist, dass der Graph
Adjazenzgraph einer zeilenstochastischen
Matrix ist.
Verwendung
Übergangsgraphen dienen zur anschaulichen Darstellung von homogenen
Markow-Ketten mit endlichem Zustandsraum in diskreter Zeit. Dabei entspricht
jeder Knoten einem Zustand des Systems und die Kantengewichte sind die Übergangswahrscheinlichkeiten
zwischen den Zuständen. Dann ist
genau die Wahrscheinlichkeit,
vom Zustand
in den Zustand
zu wechseln. Einige Eigenschaften der Markow-Kette finden sich direkt im
Übergangsgraph wieder:
- Der Übergangsgraph ist genau dann stark zusammenhängend, wenn die Markow-Kette irreduzibel ist.
- Der Zustand
ist von dem Zustand
aus erreichbar, wenn es einen
-Pfad im Übergangsgraph gibt.
- Zwei Zustände i und j kommunizieren
genau dann, wenn sowohl ein
-Pfad als auch ein
-Pfad im Übergangsgraph existiert.
- Ist der Übergangsgraph bipartit, so hat jeder Zustand der Markow-Kette gerade periode.
- Ist der Übergangsgraph bipartit und Zusammenhängend, so hat die Markow-Kette gerade Periode.
Anwendungsbeispiel
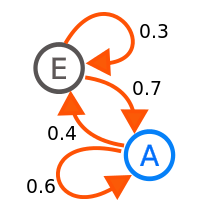
Mit Hilfe von Übergangsgraphen lässt sich das Wahl- und Kaufverhalten visualisieren. Dargestellt werden die prozentuale Zahl von Wieder- und Wechselwählern. Bezogen auf die obigen Abbildung würden 60 % der Partei bzw. dem Produkt A treu bleiben und 40 % zu Partei bzw. Produkt E wechseln. Die Zahl der Wiederwähler bei Partei bzw. Produkt E liegt bei 30 %, die Zahl der Wechselwähler bei 70 %. Allerdings wird der Übergangsgraph schon ab vier Parteien bzw. Produkten recht unübersichtlich.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.12. 2023