Gerichteter Graph

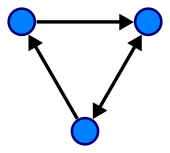
Ein gerichteter Graph mit 3 Knoten und 4 gerichteten Kanten

Ein gerichteter Graph oder Digraph (von englisch directed graph) besteht aus

einer Menge von Knoten (engl. vertex/vertices, oft auch Ecken genannt) und
einer Menge geordneter Knotenpaare $E\subseteq V\times V$ von Kanten.

Die Kanten $(v,w)\in E$ eines gerichteten Graphen sind gerichtete Kanten (engl. directed edge/edges, manchmal auch Bögen). Diese werden häufig als Pfeile dargestellt und können nur in einer Richtung durchlaufen werden. Im Gegensatz dazu sind die Kanten eines ungerichteten Graphen ungeordnete Knotenpaare $\{v,w\}$ . Gerichtete Graphen werden dazu benutzt Objekte und die dazwischenliegenden Verbindungen, beispielsweise von endlichen Automaten, darzustellen.

Grundbegriffe

Ein gerichteter Graph ohne Mehrfachkanten und Schleifen wird einfacher Digraph (auch schlichter Digraph) genannt.

Man sagt, dass eine gerichtete Kante e=(x,y) von nach geht. Dabei ist der Fuß (oder Startknoten) und der Kopf (oder Endknoten) von . Weiterhin gilt als der direkte Nachfolger von und als der direkte Vorgänger von . Falls in einem Graphen von nach einPfad führt, gilt als ein Nachfolger von und als ein Vorgänger von . Die Kante (y,x) heißt umgedrehte oder invertierte Kante von (x,y) .

Ein gerichteter Graph G heißt symmetrisch, falls G zu jeder Kante auch die entsprechende invertierte Kante enthält. Ein ungerichteter Graph lässt sich einfach in einen symmetrischen gerichteten Graphen umwandeln, indem man jede Kante $\{x,y\}$ durch die zwei gerichteten Kanten (x,y) und (y,x) ersetzt.

Um die Orientierung eines einfachen ungerichteten Graphen zu erhalten, muss jeder Kante eine Richtung zugewiesen werden. Jeder auf diese Art konstruierte gerichtete Graph wird orientierter Graph genannt. Ein einfach gerichteter Graph darf, im Gegensatz zum orientierten Graphen, zwischen zwei Knoten Kanten in beide Richtungen enthalten.

Ein gewichteter Digraph ist ein Digraph, dessen Kanten Gewichte zugeordnet werden, wodurch man einen kantengewichteten Graphen erhält. Ein Digraph mit gewichteten Kanten wird in der Graphentheorie als Netzwerk bezeichnet.

Die Adjazenzmatrix eines Digraphen (mit Schleifen und Mehrfachkanten) ist eine ganzzahlige Matrix, deren Zeilen und Spalten den Knoten des Digraphen entsprechen. Ein Eintrag $a_{ij}$ außerhalb der Hauptdiagonalen gibt die Anzahl der Kanten vom Knoten i zum Knoten j an, und der Eintrag der Hauptdiagonalen $a_{{ii}}$ entspricht der Anzahl der Schleifen im Knoten i. Die Adjazenzmatrix eines Digraphen ist bis auf Vertauschung von Zeilen und Spalten eindeutig.

Ein Digraph lässt sich auch durch eine Inzidenzmatrix repräsentieren.

Eingangs- und Ausgangsgrad

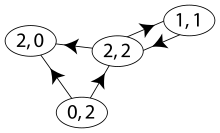
Digraph mit Knotenbeschriftung (Eingangs- und Ausgangsgrad).

→ Hauptartikel: Grad (Graphentheorie)#Gerichtete Graphen

Die Anzahl der direkten Vorgänger eines Knotens wird Eingangsgrad (auch Innengrad) und die Anzahl der direkten Nachfolger Ausgangsgrad (oder Außengrad) genannt.

Der Eingangsgrad eines Knotens in einem Graphen wird mit $d_{G}^{-}(v)$ und der Außengrad mit $d_{G}^{+}(v)$ bezeichnet. Ein Knoten mit $d_{G}^{-}(v)=0$ wird Quelle und ein Knoten mit $d_{G}^{+}(v)=0$ wird Senke genannt. Eine Senke heißt universelle Senke, falls sie eingehende Kanten von jedem anderen Knoten hat, falls also ihr Eingangsgrad gleich $\mid V\mid -1$ ist.

Für gerichtete Graphen ist die Summe aller Eingangsgrade gleich der Summe aller Ausgangsgrade, und beide gleich der Summe der gerichteten Kanten:

$\sum _{{v\in V}}d_{G}^{+}(v)=\sum _{{v\in V}}d_{G}^{-}(v)=|E|\,.$

Falls für alle Knoten $v\in V$ die Gleichung $d_{G}^{+}(v)=d_{G}^{-}(v)$ gilt, wird der Graph balancierter Digraph genannt.

Zusammenhang von Digraphen

→ Hauptartikel: Zusammenhang (Graphentheorie)

Ein gerichteter Graph heißt schwach zusammenhängend (oder nur zusammenhängend), falls der unterliegende Graph von , den man mittels Ersetzung aller gerichteter Kanten durch ungerichtete erhält, ein zusammenhängender Graph ist. Ein gerichteter Graph heißt stark zusammenhängend oder stark, wenn je zwei seiner Knoten gegenseitig erreichbar sind. Ein maximaler stark zusammenhängender Untergraph von ist eine starke Komponente.

Darstellung von gerichteten Graphen

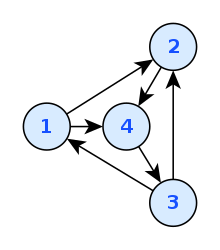
Der im Beispiel behandelte gerichtete Graph

Außer der naiven Darstellung eines gerichteten Graphen durch Angabe der Knoten- und Kantenmenge gibt es noch weitere Darstellungsmöglichkeiten, das sogenannte Kanten bzw Knotenfeld.

Kantenfeld

Ein Kantenfeld ist eine Darstellungsart für gerichtete Graphen nach folgendem Schema:

$|V|,|E|,E_{1},\ldots ,E_{{|E|}}$ ,

wobei |V| die Anzahl der Knoten, |E| die Anzahl der Kanten und $E_{1},\ldots ,E_{{|E|}}$ die Kanten mit $E_{i}=(v,w)\in E$ sind.

Knotenfeld

Ein Knotenfeld ist eine Darstellungsart für gerichtete Graphen mit folgendem Aufbau:

$|V|,|E|,{\text{ag}}(V_{1}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{{\text{ag}}(V_{1})}},\ldots ,{\text{ag}}(V_{{|V|}}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{{\text{ag}}(V_{{|V|}})}}$ ,

wobei |V| die Anzahl der Knoten, |E| die Anzahl der Kanten und ag(V) der Ausgangsgrad des Knotens sind.

Beispiel

Betrachtet man als Beispiel den rechts stehenden gerichteten Graph, so ist das Kantenfeld 4,6,(1,2),(1,4),(2,4),(3,1),(3,2),(4,3) und das Knotenfeld $4,6,{\mathbf {2}},2,4,{\mathbf {1}},4,{\mathbf {2}},1,2,{\mathbf {1}},3$ . Die fett gedruckten Zahlen geben den Ausgangsgrad an.

Klassen von Digraphen

Ein gerichteter azyklischer Graph oder azyklischer Digraph ist ein gerichteter Graph, der keinen gerichteten Kreis enthält. Spezialfälle gerichteter azyklischer Graphen sind Mehrfachbäume (je zwei gerichtete Pfade des Graphen, die vom selben Startknoten ausgehen, dürfen sich nicht im selben Endknoten treffen), orientierte Bäume oder Polybäume (Orientierung eines ungerichteten azyklischen Graphen) und Wurzelbäume (orientierte Bäume, bei denen alle Kanten des unterliegenden ungerichteten Baumes vom Wurzelknoten wegführen).

Ein Turniergraph ist eine Orientierung des vollständigen Graphen K_n .

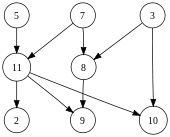
Einfach gerichteter azyklischer Graph

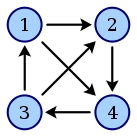
Turniergraph mit 4 Knoten

Basierend auf einem Artikel in:

Wikipedia.de