Grad (Graphentheorie)

Grad (auch Knotengrad oder Valenz) ist ein grundlegender Begriff der Graphentheorie, einem Teilgebiet der Mathematik. Der Grad eines Knotens ist die Anzahl von Kanten, die an ihn angrenzen. Dabei werden Schlingen doppelt gezählt.

Definition

Ungerichtete Graphen

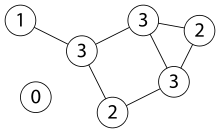
Ein ungerichteter Graph. Die Knoten sind mit ihrem Grad beschriftet.

In einem ungerichteten Graphen ist für jeden Knoten der Grad $d_{G}(v)$ definiert als

die Anzahl der Nachbarn von , falls ein Graph (oder Hypergraph) ohne Mehrfachkanten ist;
die Summe der Vielfachheiten aller mit inzidenten Kanten, falls ein Graph mit Mehrfachkanten ist.

Statt $d_{G}(v)$ wird oft auch die Notation $\deg _{G}(v)$ (engl. degree) verwendet. Der Index kann weggelassen werden, falls klar ist, um welchen Graphen es sich handelt.

Den kleinsten Grad eines Knotens in nennt man den Minimalgrad von und bezeichnet diesen mit $\delta (G)$ , den größten Grad eines Knotens in nennt man den Maximalgrad von , dieser wird meist mit $\Delta (G)$ bezeichnet. Der Durchschnitt aller Knotengrade von wird Durchschnittsgrad genannt und mit d(G) bezeichnet.

Gerichtete Graphen

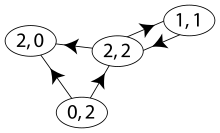
Ein gerichteter Graph mit beschrifteten Knoten: (Eingangsgrad, Ausgangsgrad)

In einem gerichteten Graphen wird unterschieden, ob eine Kante an einem Knoten beginnt oder endet. Mit $d_{G}^{-}(v)$ bezeichnet man den Eingangsgrad des Knotens in einem gerichteten Graphen und mit $d_{G}^{+}(v)$ dessen Ausgangsgrad.

Dabei ist $d_{G}^{-}(v)$ in

Graphen ohne Mehrfachkanten die Anzahl der Vorgänger von ,
Graphen mit Mehrfachkanten die Summe der Vielfachheiten aller Kanten in der Form $(v,x)$ .

und $d_{G}^{+}(v)$ in

Graphen ohne Mehrfachkanten die Anzahl der Nachfolger von ,
Graphen mit Mehrfachkanten die Summe der Vielfachheiten aller Kanten in der Form .

Einen Knoten ohne Eingangskanten ( $d_{G}^{-}(v)=0$ ) nennt man Quelle, einen Knoten ohne Ausgangskanten ( $d_{G}^{+}(v)=0$ ) nennt man Senke.

Eigenschaften

Stets gilt $\delta (G)\leq d(G)\leq \Delta (G)$ . Gleichheit tritt z.B. bei vollständigen Graphen, allgemein bei regulären Graphen ein.
Die Anzahl der Ecken mit ungeradem Grad ist stets gerade.

Verwendung

Der Grad gehört zu den Grundbegriffen der Graphentheorie und liefert viele wichtige Abschätzungen für Grapheneigenschaften wie z.B. die Kantenfärbungszahl

Basierend auf einem Artikel in: