Mittelwert
Ein Mittelwert (kurz auch nur Mittel) ist eine nach einer bestimmten Rechenvorschrift aus zwei oder mehreren Zahlen ermittelte weitere Zahl. Sie liegt zwischen den vorgegebenen Zahlen. Einige von beliebig viel berechenbaren Mittelwerten sind das Arithmetische, das Geometrische und das Quadratische Mittel.
Mittelwerte werden am häufigsten in der Statistik angewendet, wobei mit Mittel oder Durchschnitt meistens das arithmetische Mittel gemeint ist. Bei laxer Formulierung werden die Begriffe Mittelwert und Erwartungswert häufig synonym verwendet.
Definitionen der bekanntesten und wichtigsten Mittelwerte
Im Folgenden seien
gegebene reelle Zahlen, in der
Statistik etwa Messwerte, deren Mittelwert
berechnet werden soll.
| Mittelwert | Definition |
|---|---|
| Modus (Statistik) | Ausprägung mit höchster Häufigkeit |
| Median (Statistik) | Für die sortierten
Werte |
| Arithmetisches Mittel | |
| Geometrisches Mittel | |
| Harmonisches Mittel | |
| Quadratisches Mittel | |
| Kubisches Mittel |
Beispiele für die Verwendung unterschiedlicher Mittelwerte
| Merkmalsträger |
Wert |
|---|---|
| 2 (A) | |
| 2 (A) | |
| 2 (A) | |
| 3 (B) | |
| 3 (B) | |
| 4 (C) | |
| 5 (D) |
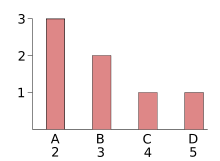
Im Folgenden soll beispielhaft an den sieben rechts angegebenen Ausprägungen gezeigt werden, wo welche Definition des Mittelwerts sinnvoll ist.
Der Modus ist bereits in der Nominalskala
sinnvoll, in der einzelne Merkmale nicht geordnet werden können. Sind etwa von
sieben befragten Personen drei katholisch (A), zwei evangelisch (B), einer
muslimisch (C) und einer Hindu (D), so liegt der Modus bei ,
denn dies kommt am häufigsten vor.
Für den Median ist eine Ordinalskala
Voraussetzung, in der die Merkmale geordnet werden können. Auf die Frage nach
der Qualität des Essens eines Restaurants antworten beispielsweise drei Kunden
mit „sehr gut“ (A), zwei mit „gut“ (B) sowie je einer mit „mittel“ und
„schlecht“ (C bzw. D). Nach Ordnen der Daten wie in der Liste rechts erkennt
man, dass die mittlere Beobachtung bei .
Das arithmetische Mittel wird beispielsweise zum Berechnen der Durchschnittsgeschwindigkeit genutzt: Läuft eine Schildkröte erst eine Stunde lang drei Meter pro Stunde, dann drei Stunden lang je zwei Meter und beschleunigt für jeweils eine Stunde nochmals auf drei, vier und fünf Meter pro Stunde, so ergibt sich als arithmetisches Mittel bei einer Strecke von 21 Metern in 7 Stunden:
Auch das harmonische Mittel kann zur Berechnung einer
durchschnittlichen Geschwindigkeit sinnvoll sein, wenn nicht über gleiche
Zeiten, sondern über gleiche Strecken gemessen wird: Die Schildkröte laufe den
1. Meter mit 3 Metern pro Stunde, weitere 3 m mit jeweils 2 m/h und
beschleunigt auf den letzten 3 Metern nochmals auf jeweils 3, 4 und 5 m/h.
Die Durchschnittsgeschwindigkeit ergibt sich bei einer Strecke von 7 Metern
in Stunden:
Mit dem geometrischen Mittel errechnet man den mittleren
Wachstumsfaktor. Eine Bakterienkultur wachse beispielsweise am ersten Tag auf
das Fünffache, am zweiten auf das Vierfache, dann zweimal auf das Dreifache und
die letzten drei Tage verdoppelt sie sich täglich. Der Bestand nach dem siebten
Tag errechnet sich also durch
Alternativ kann mit dem geometrischen Mittel der Endbestand ermittelt werden,
denn
und somit ist
Ein tägliches Wachstum der Bakterienkultur um das 2,83-Fache hätte also nach sieben Tagen zum selben Ergebnis geführt.
Geschichte
In der Mathematik treten Mittelwerte, insbesondere die drei klassischen
Mittelwerte (arithmetisches, geometrisches und harmonisches Mittel), bereits in
der Antike auf. Pappos von Alexandria
kennzeichnet 10 verschiedene Mittelwerte m von 2 Zahlen
und
(
)
durch spezielle Werte des Streckenverhältnisses
.
Auch die Ungleichung zwischen harmonischem, geometrischem und arithmetischem
Mittel ist in der Antike bereits bekannt und geometrisch interpretiert. Im 19.
und 20. Jahrhundert spielen Mittelwerte in der Analysis eine spezielle Rolle,
dort im Wesentlichen im Zusammenhang mit berühmten Ungleichungen und wichtigen
Funktionseigenschaften wie Konvexität (Hölder-Ungleichung,
Minkowski-Ungleichung,
Jensensche
Ungleichung usw.). Dabei wurden die klassischen Mittelwerte in mehreren
Schritten verallgemeinert, zunächst zu den Potenzmittelwerten (siehe
Abschnitt Hölder-Mittel
unten) und diese wiederum zu den quasi-arithmetischen
Mittelwerten. Die klassische Ungleichung zwischen harmonischem,
geometrischem und arithmetischem Mittel geht dabei über in allgemeinere
Ungleichungen zwischen Potenzmittelwerten bzw. quasi-arithmetischen
Mittelwerten.
Gemeinsame Definition der drei klassischen Mittelwerte
Die Idee, die den drei klassischen Mittelwerten zugrunde liegt, lässt sich auf folgende Weise allgemein formulieren:
Beim arithmetischen Mittel sucht man die Zahl ,
für die
gilt, wobei sich die Summe links über
Summanden erstreckt. Das arithmetische Mittel mittelt also bzgl. der
arithmetischen Verknüpfung „Summe“. Anschaulich bestimmt man mit dem
arithmetischen Mittel aus Stäben verschiedener Länge einen mit einer
durchschnittlichen oder mittleren Länge.
Beim geometrischen Mittel sucht man die Zahl ,
für die
gilt, wobei sich das Produkt links über
Faktoren erstreckt. Das geometrische Mittel mittelt also bzgl. der
arithmetischen Verknüpfung „Produkt“.
Das harmonische Mittel
löst die Gleichung
Zusammenhänge
Der Kehrwert des harmonischen Mittels ist gleich dem arithmetischen Mittel der Kehrwerte der Zahlen.
Für
hängen die Mittelwerte untereinander in folgender Weise zusammen:
oder nach dem geometrischen Mittel aufgelöst
- IMG class="text" style="width: 24.56ex; height: 3ex; vertical-align: -1.17ex;" alt="x_{{\text{geom}}}={\sqrt {x_{{\text{arithm}}}\cdot x_{{\text{harm}}}}}." src="/svg/d3d457a7a895b1b91cae934c48ea87581a154680.svg">
Ungleichung der Mittelwerte
Die Ungleichung von arithmetischen und geometrischen Mittel vergleicht die Werte des arithmetischen und geometrischen Mittels zweier gegebener Zahlen: Es gilt für positive Variable stets
Die Ungleichung lässt sich auch auf weitere Mittelwerte ausdehnen, z.B. (für positive Variable)
Für zwei (positive) Variablen gibt es auch eine grafische Veranschaulichung:
-
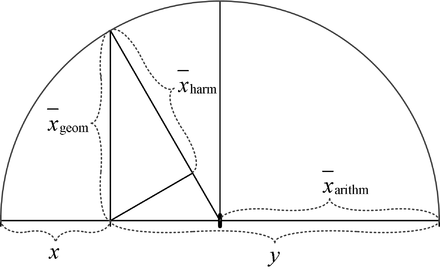 geometrischer Beweis der Ungleichung für Mittelwerte zweier Variablen
geometrischer Beweis der Ungleichung für Mittelwerte zweier Variablen
Das geometrische Mittel folgt direkt aus dem euklidischen Höhensatz und das harmonische Mittel aus dem euklidischen Kathetensatz mit der Beziehung
Weitere Mittelwerte und ähnliche Funktionen
Gewichtete Mittel
Die gewichteten oder auch gewogenen Mittelwerte entstehen, wenn man den einzelnen Werten unterschiedliche Gewichte zuordnet, mit denen sie in das Gesamtmittel einfließen; zum Beispiel wenn bei einer Prüfung mündliche und schriftliche Leistung unterschiedlich stark in die Gesamtnote einfließen.
Die genauen Definitionen finden sich hier:
Logarithmischer Mittelwert
Der logarithmische
Mittelwert
zwischen
und
ist definiert als:
Für
liegt der logarithmische Mittelwert zwischen dem geometrischen und dem
arithmetischen Mittelwert.
Winsorisiertes oder gestutztes Mittel
Kann man davon ausgehen, dass die Daten durch „Ausreißer“,
das heißt einige wenige zu hohe oder zu niedrige Werte, kontaminiert sind, so
kann man die Daten entweder durch Stutzen oder durch „Winsorisieren“ (benannt
nach Charles
P. Winsor) bereinigen und den gestutzten
(engl. truncated mean) oder winsorisierten Mittelwert
(engl. Winsorized mean) berechnen. In beiden Fällen sortiert
man die Beobachtungswerte zuerst nach aufsteigender Größe. Beim Stutzen
schneidet man sodann eine gleiche Anzahl von Werten am Anfang und am Ende der
Folge ab und berechnet von den übrig bleibenden Werten den Mittelwert. Hingegen
werden beim „Winsorisieren“ die Ausreißer am Anfang und Ende der Folge durch den
nächstgrößeren (bzw. -kleineren) Wert der restlichen Daten ersetzt.
Beispiel: Hat man 10 aufsteigend sortierte, reelle Zahlen ,
so ist das 10 %-gestutzte Mittel gleich
Indes ist der 10-%-winsorisierte Mittelwert gleich
D.h. das gestutzte Mittel liegt zwischen dem arithmetischen Mittel (keine Stutzung) und dem Median (maximale Stutzung). Üblicherweise wird ein 20 % gestutztes Mittel verwendet, d.h. 40 % der Daten bleiben unberücksichtigt für die Mittelwertberechnung. Die Prozentzahl richtet sich im wesentlich nach der Zahl der vermuteten Ausreißer in den Daten; für Bedingungen für eine Stutzung von weniger als 20 % sei auf die Literatur verwiesen.
Quartilsmittel
Das Quartilsmittel ist definiert als der Mittelwert des 1. und 3. Quartils:
Hierbei bezeichnet
das 25 %-Quantil (1. Quartil) und
entsprechend
das 75 %-Quantil (3. Quartil) der Messwerte.
Das Quartilsmittel ist robuster als das arithmetische Mittel, aber weniger robust als der Median.
Mitte der kürzesten Hälfte
Sei
das kürzeste Intervall unter allen Intervallen mit
,
so ist
dessen Mitte (middle of the shortest half). Bei unimodalen symmetrischen
Verteilungen konvergiert dieser Wert gegen das arithmetische Mittel.
Gastwirth-Cohen-Mittel
Das Gastwirth-Cohen-Mittel nutzt drei Quantile der Daten: das
Quantil und das
Quantil jeweils mit Gewicht
sowie den Median mit Gewicht
:
mit
und
.
Spezialfälle sind
- das Quartilsmittel mit
,
und
- das Trimean mit
,
.
Bereichsmittel
Das Bereichsmittel ist definiert als der Mittelwert des größten und kleinsten Beobachtungswerts:
oder
Das „a-Mittel“
Für einen gegebenen reellen Vektor
mit
wird der Ausdruck
wobei über alle Permutationen
von
summiert wird, als „
-Mittel“
[
]
der nichtnegativen reellen Zahlen
bezeichnet.
Für den Fall ,
ergibt das genau das arithmetische Mittel der Zahlen
;
für den Fall IMG class="text"
style="width: 16.01ex; height: 4.84ex; vertical-align: -1.83ex;"
alt="a=\left({\tfrac 1n},\dots ,{\tfrac 1n}\right)" src="/svg/016403f618c606a76911dc3435241a9bc7928179.svg">
ergibt sich genau das geometrische Mittel.
Für die -Mittel
gilt die Muirhead-Ungleichung.
Beispiel: Sei
und
dann gilt
und die Menge der Permutationen (in Kurzschreibweise) von
ist
Damit ergibt sich
Gleitende Durchschnitte
Gleitende Durchschnitte werden in der dynamischen Analyse von Messwerten angewandt. Sie sind außerdem ein gängiges Mittel der technischen Analyse in der Finanzmathematik. Mit gleitenden Durchschnitten kann das stochastische Rauschen aus zeitlich voranschreitenden Signalen herausgefiltert werden. Häufig handelt es sich dabei um FIR-Filter. Jedoch muss beachtet werden, dass die meisten gleitenden Durchschnitte dem echten Signal hinterherlaufen. Für vorausschauende Filter siehe z.B. Kalman-Filter.
Gleitende Durchschnitte benötigen normalerweise eine unabhängige Variable, die die Größe der nachlaufenden Stichprobe bezeichnet, bzw. das Gewicht des vorangehenden Wertes für die exponentiellen gleitenden Durchschnitte.
Gängige gleitende Durchschnitte sind:
- arithmetische gleitende Durchschnitte (Simple Moving Average – SMA),
- exponentiell gleitende Durchschnitte (Exponential Moving Average – EMA),
- doppelt exponentiell gleitende Durchschnitte (Double EMA, DEMA),
- dreifach,
-fach exponentiell gleitende Durchschnitte (Triple EMA – TEMA),
- linear gewichtete gleitende Durchschnitte (linear abfallende Gewichtung),
- quadratisch gewichtete gleitende Durchschnitte und
- weitere Gewichtungen: Sinus, Triangular, …
In der Finanzliteratur können außerdem sogenannte adaptive gleitende Durchschnitte gefunden werden, die sich automatisch einer sich ändernden Umgebung (andere Volatilität/Streuung etc.) anpassen:
- Kaufmann’s Adaptive Moving Average (KAMA) sowie
- Variable Index Dynamic Average (VIDYA).
Sonstige Mittelwerte
Sonstige Mittelwerte, die in einem eigenen Artikel beschrieben werden, sind der Modus (eigentlich kein Mittelwert, sondern der häufigste Wert) und der Median, der robust gegenüber extremen Abweichungen, sogenannten Ausreißern, ist.
Außerdem lassen sich Mittelwerte kombinieren; so entsteht etwa das arithmetisch-geometrische Mittel, das zwischen dem arithmetischen und geometrischen Mittel liegt.
Verallgemeinerte Mittelwerte
Es gibt eine Reihe weiterer Funktionen, mit denen sich die bekannten und weitere Mittelwerte erzeugen lassen.
Hölder-Mittel
Für positive
Zahlen
definiert man den -->
-Potenzmittelwert,
auch Hölder-Mittel (englisch
-th
power mean) als
Für
= 0 ist der Wert durch stetige
Ergänzung definiert:
Man beachte, dass sowohl Notation als auch Bezeichnung uneinheitlich sind.
Für
= −1, 0, 1, 2 und 3 ergeben sich daraus etwa das harmonische, das geometrische,
das arithmetische, das quadratische und das kubische Mittel. Für
→ -∞ ergibt sich das Minimum, für
→ +∞ das Maximum der Zahlen.
Außerdem gilt bei festen Zahlen :
Je größer
ist, desto größer ist
;
daraus folgt dann die verallgemeinerte Ungleichung der Mittelwerte
Lehmer-Mittel
Das Lehmer-Mittel
ist ein anderer verallgemeinerter Mittelwert; zur Stufe
ist es definiert durch
Es hat die Spezialfälle
ist das harmonische Mittel;
ist das geometrische Mittel von
und
;
ist das arithmetische Mittel;
Stolarsky-Mittel
Das Stolarsky-Mittel
zweier Zahlen
ist definiert durch
Integraldarstellung nach Chen
Die Funktion
ergibt für verschiedene Argumente
die bekannten Mittelwerte von
:
ist das harmonische Mittel
ist das geometrische Mittel
ist das arithmetische Mittel
Aus der Stetigkeit und Monotonie der so definierten Funktion
folgt die Mittelwertungleichung
Mittelwert einer Funktion
Das arithmetische Mittel einer stetigen Funktion
in einem geschlossenen Intervall
ist
, wobei
die Zahl der Stützstellen ist.
Das quadratische Mittel einer stetigen Funktion ist
Diese finden in der Technik erhebliche Beachtung, siehe Gleichwert und Effektivwert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.03. 2021