Ordnungsstatistik

In der Statistik bezeichnet die -te Ordnungsstatistik (auch Ordnungsgröße genannt) den -kleinsten Wert einer Stichprobe. Ordnungsstatistiken sind damit spezielle Zufallsvariablen. Sie werden aus einer vorgegebenen Gruppe von Zufallsvariablen gewonnen und modifizieren diese so, dass die Realisierungen der Ordnungsstatistik den Realisierungen der zugrunde liegenden Zufallsvariablen entsprechen, aber immer der Größe nach geordnet sind.

Daher treten Ordnungsstatistiken insbesondere bei der Untersuchung von zufälligen Strukturen auf, die mit einer Ordnung versehen sind. Dazu zählt beispielsweise die Analyse von Wartezeitprozessen oder die Bestimmung von Schätzfunktionen für den Median oder Quantile.

Definition

Gegeben seien Zufallsvariablen $X_{1},X_{2},\dots ,X_{n}$ . Sind die Zufallsvariablen bindungsfrei, nehmen also fast sicher nicht denselben Wert an, formell ausgedrückt

$i\neq j$ ,

so definiert man

$X_{1:n}:=\min\{X_{1},\dots ,X_{n}\}$

und

$X_{j:n}:=\min\{X_{i}\mid X_{i}>X_{(j-1):n}\}$

für $j=2,\dots ,n$ . Dann heißen $X_{1:n},X_{2:n},\dots ,X_{n:n}$ die Ordnungsstatistiken von $X_{1},X_{2},\dots ,X_{n}$ . Die Zufallsvariable $X_{j:n}$ wird dann auch die -te Ordnungsstatistik genannt. Als alternative Notation wird auch $X_{(j)}$ anstelle von $X_{j:n}$ verwendet.

Sind die Zufallsvariablen nicht bindungsfrei, so lassen sich die Ordnungsstatistiken definieren als

$X_{j:n}:=\min \left\{c\in \mathbb {R} \mid \sum _{i=1}^{n}\mathbf {1} _{\{X_{i}\leq c\}}\geq j\right\}$ .

Hierbei bezeichnet $\mathbf {1} _{A}$ die Indikatorfunktion auf der Menge . Im bindungsfreien Fall stimmen beide Definitionen überein. Nicht alle Autoren fordern wie oben, dass die Zufallsvariablen fast sicher ungleiche Werte annehmen. Die Eigenschaften der Ordnungsstatistiken variieren dann leicht.

Eigenschaften

Fordert man in der Definition

$P(X_{i}\neq X_{j})=1$ für alle $i\neq j$ ,

so gilt

$X_{1:n}<X_{2:n}<\dots <X_{n:n}$ fast sicher.

Äquivalent dazu gilt für die Realisierungen

$X_{1:n}(\omega )<X_{2:n}(\omega )<\dots <X_{n:n}(\omega )$ für fast alle Ereignisse $\omega$ .

Die Realisierungen der Ordnungsstatistiken sind also (fast sicher) strikt aufsteigend.

Verzichtet man auf die Forderung, dass die Zufallsvariablen fast sicher nicht dieselben Werte annehmen sollen, so gilt entsprechend

$X_{1:n}\leq X_{2:n}\leq \dots \leq X_{n:n}$ fast sicher.

Die Realisierungen sind dann nur noch (fast sicher) aufsteigend.

Verteilung der Ordnungsstatistiken

Für die Verteilungsfunktion der -ten Ordnungsstatistik gilt

$F_{X_{i:n}}(y)=\sum _{j=i}^{n}{\binom {n}{j}}F(y)^{j}\left[1-F(y)\right]^{n-j},\quad y\in \mathbb {R} ,\ 1\leq i\leq n,\ F=F_{X}.$

Wichtige Spezialfälle der Verteilung ergeben sich für das Minimum ( i=1 ) und Maximum ( $i=n$ ) als

$F_{X_{1:n}}(y)=1-\left[1-F(y)\right]^{n}{\text{ bzw.}}$

$F_{X_{n:n}}(y)=\left[F(y)\right]^{n}.$

Hat die Verteilung von eine Dichtefunktion f_X , dann erhält man durch Differenzieren die Dichtefunktion

$f_{X_{i:n}}(y)={\frac {n!}{(i-1)!(n-i)!}}f_{X}(y)\left[F_{X}(y)\right]^{i-1}\left[1-F_{X}(y)\right]^{n-i}$

der -ten Ordnungsstatistik.

Anwendung

In der nichtparametrischen Statistik lassen sich Rangstatistiken oder empirische Verteilungsfunktionen durch Ordnungsstatistiken ausdrücken. Zudem können aus Ordnungsstatistiken schwach konsistente Schätzer für Quantile abgeleitet werden. Weiter lassen sich durch oben genannte Verteilung über Faltungen und Transformationssätze die Verteilung von wichtigen Maßzahlen wie dem Median oder der Spannweite gewinnen.

Beispiel

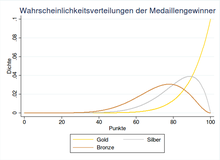
Wahrscheinlichkeitsdichten der Ränge 10 (Gold), 9 (Silber) und 8 (Bronze)

Es wird das Finale eines Wettbewerbs der Leichtathletik, bestehend aus den besten Teilnehmern, ausgetragen. In diesem Beispiel wird angenommen, dass die Leistungsdichte im Finale des Wettkampfes sehr groß ist und es daher keine Favoriten für die Medaillen gibt. Für die zufällige Gesamtpunktzahl jedes Athleten wird daher dieselbe stetige Gleichverteilung im Punktebereich von $0$ bis 100 angenommen. Es entscheidet demnach ausschließlich die Tagesform über die Gesamtpunktzahl, welche starken Schwankungen unterliegt, und alle Athleten besitzen das gleiche Leistungspotential. Setzt man die Dichtefunktion $f_{X}(x)={\frac {1}{100}}\cdot I_{[0,100]}(x)$ und die Verteilungsfunktion

$F_{X}(x)={\begin{cases}0&x<0\\{\frac {x}{100}}\cdot I_{[0,100]}(x)&0\leq x\leq 100\\1&x>100\end{cases}}$

der stetigen Gleichverteilung in die obige Dichtefunktion der Ordnungsstatistik ein, erhält man die Verteilungen für die einzelnen Ränge. Da die Punktzahlen in der Ordnungsstatistik aufsteigend sortiert sind, erhält man für $i=10$ die Wahrscheinlichkeitsverteilung für die Goldmedaille, für $i=9$ die der Silbermedaille und für $i=8$ die der Bronzemedaille. Der nebenstehenden Grafik ist bereits zu entnehmen, dass für die Goldmedaille eine höhere Punktzahl zu erwarten ist als für die Silber- oder Bronzemedaille. Da die Punkte in diesem Beispiel als stetige Gleichverteilung modelliert wurden, ist die -te Ordnungsstatistik für $i=1,...,n$ (siehe Grafik) jeweils Beta-verteilt (multipliziert mit 100 ) mit den Parametern und $11-i$ . Der Erwartungswert einer solchen Betaverteilung ist ${\frac {i}{11}}$ . Für die Goldmedaille ist daher eine Punktzahl von , für Silber $82$ und für Bronze zu erwarten. Falls ein Athlet bereits Punkte erhalten hat und auf die Punktzahlen der anderen Sportler wartet, kann er unter den gemachten Annahmen seine eigenen Chancen für Gold berechnen. Die Wahrscheinlichkeit, dass die anderen Athleten alle schlechter abschneiden, beträgt $\left({\frac {p}{100}}\right)^{9}$ . Falls der Athlet insgesamt Punkte erhält, wie für die Goldmedaille erwartet, wird er also trotzdem nur mit einer Wahrscheinlichkeit von $42,8\,\%$ die Goldmedaille bekommen.

Literatur

Herbert Büning und Götz Trenkler: Nichtparametrische statistische Methoden. 2. Auflage, de Gruyter, Berlin und New York 1994, ISBN 3-11-016351-9

Basierend auf einem Artikel in:

Wikipedia.de