
Beta-Verteilung
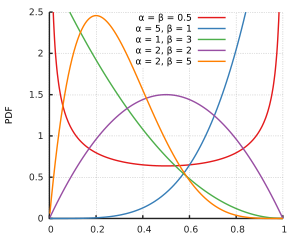
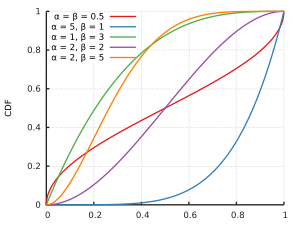
Die Beta-Verteilung ist eine Familie stetiger Wahrscheinlichkeitsverteilungen
über dem Intervall
,
parametrisiert durch zwei Parameter, die häufig als p und q – oder
auch als α und β – bezeichnet werden.
In der bayesschen
Statistik ist die Beta-Verteilung die konjugierte
a-priori-Wahrscheinlichkeitsverteilung für die Bernoulli-, Binomial-, der
negativen Binomial- und der geometrischen Verteilung.
Definition
Die Beta-Verteilung
ist definiert durch die Wahrscheinlichkeitsdichte
Außerhalb des Intervalls
wird sie durch
fortgesetzt. Für
lässt sich
durch
ersetzen. Die Beta-Verteilung besitzt die reellen Parameter
und
(in den nebenstehenden Grafiken
und
).
Um ihre Normierbarkeit zu garantieren, wird
(bzw.
)
gefordert.
Der Vorfaktor
dient der korrekten Normierung. Der Ausdruck
steht für die Betafunktion,
nach der die Verteilung benannt ist. Dabei bezeichnet
die Gammafunktion.
Die Verteilungsfunktion ist entsprechend
mit
Die Funktion
heißt auch regularisierte unvollständige Betafunktion.
Eigenschaften
Erwartungswert
Der Erwartungswert berechnet sich zu
.
Modus
Der Modus,
also die Maximalstelle der Dichtefunktion ,
ist für
,
.
Varianz
Die Varianz ergibt sich zu
.
Standardabweichung
Für die Standardabweichung ergibt sich
.
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten
.
Schiefe
Die Schiefe ergibt sich zu
.
Höhere Momente
Aus der momenterzeugenden Funktion ergibt sich für die k-ten Momente
.
Symmetrie
Die Beta-Verteilung ist für
symmetrisch
um
mit der Schiefe
.
Momenterzeugende Funktion
Die momenterzeugende Funktion einer betaverteilten Zufallsgröße lautet
.
Mit der hypergeometrischen
Funktion
erhält man die Darstellung
.
Charakteristische Funktion
Analog zur momenterzeugenden Funktion erhält man die charakteristische Funktion
.
Beziehungen zu anderen Verteilungen
Spezialfälle
- Für
ergibt sich als Spezialfall die stetige Gleichverteilung.
- Für
ergibt sich als Spezialfall die Arcsin-Verteilung.
Beziehung zur Gammaverteilung
Wenn
und
unabhängige gammaverteilte
Zufallsvariablen sind mit den Parametern
bzw.
,
dann ist die Größe
betaverteilt mit Parametern
und
,
kurz
Beziehung zur stetigen Gleichverteilung
Sind
unabhängige auf
stetig
gleichverteilte Zufallsvariable, dann sind die Ordnungsstatistiken
betaverteilt. Genauer gilt
für .
Mischverteilungen
Eine Binomialverteilung,
deren Parameter
betaverteilt ist, nennt man Beta-Binomialverteilung.
Dies ist ein spezieller Fall einer Mischverteilung.
Beispiel
Die Beta-Verteilung kann aus zwei Gammaverteilungen
bestimmt werden: Der Quotient
aus den stochastisch unabhängigen Zufallsvariablen
und
,
die beide gammaverteilt sind mit den Parametern
und
bzw.
,
ist betaverteilt mit den Parametern
und
.
und
lassen sich als Chi-Quadrat-Verteilungen
mit
bzw.
Freiheitsgraden
interpretieren.
Mit Hilfe der linearen
Regression wird eine geschätzte Regressionsgerade
durch eine „Punktwolke“
mit
Wertepaaren
zweier statistischer Merkmale
und
gelegt, und zwar so, dass die Quadratsumme der senkrechten Abstände der
-Werte
von der Geraden
minimiert wird.
Die Streuung der Schätzwerte
um ihren Mittelwert
kann durch
gemessen werden und die Streuung der Messwerte
um ihren Mittelwert kann durch
gemessen werden. Erstere stellt die „(durch die Regression) erklärte
Quadratsumme“ (sum of squares explained, kurz: SSE) und
letztere stellt die „totale
Quadratsumme“ (sum of squares total, kurz: SST) dar. Der Quotient
dieser beiden Größen ist das Bestimmtheitsmaß:
.
Die „(durch die Regression) nicht erklärte Quadratsumme“ bzw. die „Residuenquadratsumme“
(residual sum of squares, kurz SSR) ist durch
gegeben. Durch die Quadratsummenzerlegung
lässt sich das Bestimmtheitsmaß auch darstellen als
.
Es ist also betaverteilt. Da das Bestimmtheitsmaß das Quadrat des Korrelationskoeffizienten
von
darstellt (
),
ist auch das Quadrat des Korrelationskoeffizienten betaverteilt. Allerdings kann
die Verteilung des Bestimmtheitsmaßes beim globalen
F-Test durch die F-Verteilung
angegeben werden, die tabelliert vorliegt.
Verallgemeinerung: Beta-Verteilung auf (a,b)
Definition
Die allgemeine Beta-Verteilung ist definiert durch die Wahrscheinlichkeitsdichte
wobei
und
die obere und untere Grenze des Intervalls sind. Entsprechend ergibt sich die
Berechnung von
zu
Eigenschaften
Ist
betaverteilt auf dem Intervall
mit Parametern
,
,
dann ist
betaverteilt auf dem Intervall
mit den gleichen Parametern
,
.
Ist umgekehrt
betaverteilt auf
,
dann ist
betaverteilt auf .
Beispiel
Im Dreieckstest werden drei
Proben im gleichseitigen Dreieck angeordnet, wobei eine Ecke des gedachten
Dreiecks nach oben zeigt. Zwei der drei Proben gehören zum Produkt A und eine
Probe gehört zum Produkt B oder umgekehrt. Die Aufgabe des Probanden besteht nun
darin, dasjenige Produkt zu finden, das nur einmal vorkommt. Die
Wahrscheinlichkeit durch bloßes Raten die richtige Antwort zu geben beträgt
.
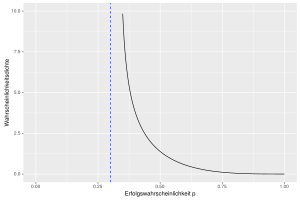
Die Erfolgswahrscheinlichkeiten variieren je nach sensorischen Fähigkeiten.
Unter der Annahme, dass kein Proband absichtlich eine falsche Antwort gibt,
liegt die Erfolgswahrscheinlichkeit bei niemandem unter .
Bei Feinschmeckern oder großen Geschmacksunterschieden kann diese theoretisch
bis auf 100 % ansteigen. Im Folgenden wird für beliebige
Rate-Erfolgswahrscheinlichkeiten
mit
die Beta-Verteilung auf
hergeleitet.
Aus den eben genannten Gründen modelliert diese Wahrscheinlichkeitsdichte die
Erfolgswahrscheinlichkeiten der Probanden realistischer als eine Beta-Verteilung
auf
.
Die Erfolgswahrscheinlichkeiten
der einzelnen Probanden
seien zunächst betaverteilt auf
mit Parametern
und
.
Die korrigierten Erfolgswahrscheinlichkeiten auf
ergeben sich aus
.
Die Wahrscheinlichkeitsdichte von
lässt sich über den Transformationssatz
für Dichten bestimmen. Die Beta-Verteilung von
hat eine positive Dichte im Intervall
.
Die Transformation
mit
ist ein Diffeomorphismus. Daraus erhält man die Umkehrfunktion
.
Für die gesuchte Dichtefunktion von
erhält man
.
Diese Wahrscheinlichkeitsdichte von
auf
wird in Abhängigkeit von der Wahrscheinlichkeitsdichte von
auf
dargestellt. In der nebenstehenden Grafik ist beispielhaft eine Beta-Verteilung
auf
mit Parametern
und
eingezeichnet. Der Erwartungswert beträgt
.
Die durchschnittliche Erfolgswahrscheinlichkeit liegt damit
über der Rate-Erfolgswahrscheinlichkeit von
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.11. 2022