Binomialtest

Ein Binomialtest ist ein statistischer Test, bei dem die Teststatistik binomialverteilt ist. Er wird verwendet, um Hypothesen über Merkmale zu prüfen, die genau zwei Ausprägungen annehmen können (dichotome Merkmale).

Hypothesen und Teststatistik

Mit dem Binomialtest können folgende Hypothesenpaare für die unbekannte Wahrscheinlichkeit eines Merkmals in der Grundgesamtheit getestet werden:

Test	$H_{0}$	$H_{1}$
zweiseitig	$p=p_{0}\,$	$p\neq p_{0}$
rechtsseitig	$p=p_{0}$ oder $p\leq p_{0}$	$p>p_{0}$
linksseitig	$p=p_{0}$ oder $p\geq p_{0}$	$p<p_{0}$

Die Teststatistik gibt an, wie oft das Merkmal in einer zufälligen Stichprobe vom Umfang aufgetreten ist. Unter der Nullhypothese $H_{0}\colon p=p_{0}$ ist die Teststatistik $B(p_{0},n)$ -verteilt, das heißt

$P(X=i)=B(i|p_{0},n)={\binom {n}{i}}p_{0}^{i}(1-p_{0})^{{n-i}}$ .

Signifikanzniveau und kritische Werte

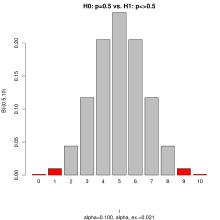
Teststatistik für den Binomialtest, die roten Säulen gehören zum kritischen Bereich.

Da die Teststatistik diskret verteilt ist, kann das vorgegebene Signifikanzniveau $\alpha$ in der Regel nicht eingehalten werden. Daher wird gefordert, die kritischen Werte so zu wählen, dass für ein möglichst großes exaktes Signifikanzniveau $\alpha _{{\text{ex}}}$ gilt $\alpha _{{\text{ex}}}\leq \alpha$ .

Für den zweiseitigen Test werden daher als kritische Werte das größte $c_{1}$ und das kleinste $c_{2}$ bestimmt werden, für die gilt

$\sum _{{i=0}}^{{c_{1}}}B(i|p_{0},n)\leq \alpha /2$ und
$\sum _{{i=c_{2}}}^{n}B(i|p_{0},n)\leq \alpha /2$ .

Das exakte Signifikanzniveau ergibt sich als $\alpha _{{\text{ex}}}=\sum _{{i=0}}^{{c_{1}}}B(i|p_{0},n)+\sum _{{i=c_{2}}}^{n}B(i|p_{0},n)$ . Für die beiden einseitigen Tests wird analog verfahren.

Test	Kritische Werte	Kritischer Bereich	Grenze(n)
zweiseitig	$c_{1}+1$ und $c_{2}-1$	$\{0,\dotsc ,c_{1}\}\cup \{c_{2},\dotsc ,n\}$
rechtsseitig		$\{c,\dotsc ,n\}$	c = kleinster Wert, für den $\sum _{{i=c}}^{n}B(i\|p_{0},n)=\alpha _{{\text{ex}}}\leq \alpha$
linksseitig		$\{0,\dotsc ,c\}$	c = größter Wert, für den $\sum _{{i=0}}^{{c}}B(i\|p_{0},n)=\alpha _{{\text{ex}}}\leq \alpha$

Approximation der Verteilung der Teststatistik

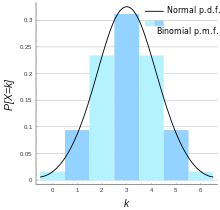
Approximation einer Binomialverteilung mit einer Normalverteilung.

Die binomialverteilte Teststatistik kann mit einer anderen Verteilung approximiert werden. Die dafür notwendigen Approximationsbedingungen können je nach Literaturquelle variieren.

Verteilung	Parameter	Approximationsbedingungen
Poisson-Verteilung $X\approx Po(\lambda )$	$\lambda =np_{0}$	und $p_{0}<0{,}05$
Normalverteilung $X\approx N(\mu ,\sigma ^{2})$	$\mu =np_{0}$ und $\sigma ^{2}=np_{0}(1-p_{0})$	$np_{0}(1-p_{0})>9$

Im Fall der Approximation der Normalverteilung kann statt der Teststatistik auch gleich die Teststatistik $\Pi =X/n\approx N\left(p_{0},{\tfrac {p_{0}(1-p_{o})}{n}}\right)$ betrachtet werden.

Beispiele

Hellseherische Fähigkeit versus Raten der Farbe einer zufällig gewählten Spielkarte (aus statistischer Test): Bei -maliger Durchführung erreicht eine Testperson Treffer (Farbe richtig genannt). Ab welcher Trefferzahl sollte man die Nullhypothese $H_{0}\colon p={\tfrac 14}$ verwerfen und die Alternativhypothese $H_{1}\colon p>{\tfrac 14}$ (also tatsächliche hellseherische Fähigkeit) für plausibler halten?^[1] Wenn $H_{0}$ richtig ist, dann ist binomialverteilt mit Parametern und 1/4. Die Wahrscheinlichkeit, oder mehr Treffer durch Raten zu erzielen, beträgt dann $\sum _{{i=k}}^{n}B(i|{\tfrac {1}{4}},n)$ . Bei einem Signifikanzniveau von 1 % verwirft man die Nullhypothese, falls $X\geq c$ . Hier ist der kleinste Wert, für den $\sum _{i=c}^{n}B(i|{\tfrac {1}{4}},n)\leq 1\,\%$ ist. Beispielsweise für ergibt sich . Die Testperson müsste also unter den genannten Bedingungen mindestens bei 36 von 100 Versuchen richtig liegen, damit ihre hellseherischen Fähigkeiten für plausibel gehalten werden.
In einer Multiple-Choice-Prüfung gibt es 50 Fragen und jeweils 4 Antwortmöglichkeiten, von denen jeweils genau eine richtig ist. Dies führt zur gleichen Fragestellung wie das Spielkartenbeispiel. Die Nullhypothese ist, dass ein Prüfling die Antwort zufällig ankreuzt ( $H_{0}\colon p=1/4$ ), und die Alternativhypothese ist $H_{1}\colon p>1/4$ .^[2] Diese Modellierung setzt allerdings voraus, dass es keine Möglichkeit gibt, gewisse Antworten als unplausibel auszuschließen.
Eine Urne enthält 10 Kugeln, von denen jede weiß oder schwarz sein kann. Man möchte die Nullhypothese testen, dass alle Kugeln weiß sind (also $H_{0}\colon p=0$ ), und zieht Kugeln mit Zurücklegen. Die Alternativhypothese ist $H_{1}\colon p>0$ und man verwirft die Nullhypothese, sobald eine oder mehr schwarze Kugeln gezogen worden sind: Der Ablehnungsbereich ist $\{1,\dotsc,n\}$ . Der Fehler 1. Art ist gleich 0, da unter der Nullhypothese keine schwarze Kugel gezogen werden kann. Der Ablehnungsbereich ist also offenbar unabhängig vom Signifikanzniveau. Der Fehler 2. Art ist maximal, falls genau eine schwarze Kugel vorhanden ist, und beträgt dann $0{,}9^{n}$ .
(Gegenbeispiel) Gleiche Situation, aber Ziehen ohne Zurücklegen (es werden maximal Kugeln gezogen). Wie im vorigen Fall verschwindet der Fehler 1. Art. Der Fehler 2. Art bestimmt sich aber aus einer hypergeometrischen Verteilung. Er ist maximal für eine schwarze Kugel und beträgt dann $(10-n)/10$ . Es handelt sich also nicht um einen Binomialtest.
Mit dem Dreieckstest möchte man herausfinden, ob es einen Geschmacksunterschied zwischen zwei Produkten und gibt. Hierfür werden drei Proben im gleichseitigen Dreieck angeordnet, wobei eine Ecke des gedachten Dreiecks nach oben zeigt. Zwei der drei Proben gehören zum Produkt und eine Probe gehört zum Produkt oder umgekehrt. Die Aufgabe des Probanden besteht nun darin, dasjenige Produkt zu finden, das nur einmal vorkommt. Die Wahrscheinlichkeit durch bloßes Raten die richtige Antwort zu geben beträgt ${\frac {1}{3}}$ . Insgesamt nehmen verschiedene Probanden an dem Versuch teil. Die statistischen Berechnungen entsprechen denen des ersten Beispiels mit dem Unterschied, dass der zu testende Parameter ${\frac {1}{3}}$ statt $\frac{1}{4}$ lautet.

Anmerkungen

↑ Wir betrachten für p den Parameterbereich [1/4,1], um zu erreichen, dass Nullhypothese und Alternativhypothese den gesamten Parameterbereich überdecken. Bei absichtlichem Nennen einer falschen Farbe könnte man zwar auch auf hellseherische Fähigkeiten schließen, aber wir nehmen an, dass die Testperson eine möglichst hohe Trefferzahl erzielen will.
↑ Wie im Spielkartenbeispiel nehmen wir an, dass der Parameterbereich [1/4,1] ist (Prüfling möchte eine möglichst hohe Trefferzahl erreichen).

Literatur

Norbert Henze: Stochastik für Einsteiger. 8. Auflage. Vieweg, 2010.
Ulrich Krengel: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 8. Auflage. Vieweg, 2005.
Horst Rinne: Taschenbuch der Statistik. 3. Auflage. Harri Deutsch, 2003.

Basierend auf einem Artikel in:

Wikipedia.de