Totale Quadratsumme

Die Summe der blauen Abweichungsquadrate ist die totale Quadratsumme.

In der Statistik, und dort insbesondere in der Regressionsanalyse, ist die gesamte bzw. totale Quadratsumme (Summe der Quadrate der Totalen Abweichungen, kurz SQT bzw. englisch sum of squared total deviations, kurz SST oder total sum of squares, kurz TSS), auch als totale Abweichungsquadratsumme, oder Gesamtabweichungsquadratsumme bezeichnet und mit SAQ_y (für Summe der Abweichungsquadrate der y-Werte) bzw. SAQ_Gesamt abgekürzt, die Quadratsumme der abhängigen Variablen. Sie wird berechnet als Summe der Quadrate der zentrierten Messwerte der abhängigen Variablen und kann als „Gesamtvariation“ bzw. „totale Variation der abhängigen Variablen $\{y_{i}\}$ “ interpretiert werden. Die totale Quadratsumme wird im Kontext der Quadratsummenzerlegung auch als zu erklärende Abweichungsquadratsumme bezeichnet. Über die genaue Bezeichnung und ihre Abkürzungen gibt es international keine Einigkeit. In der deutschsprachigen Literatur wird manchmal die deutsche Bezeichnung mit englischen Abkürzungen gebraucht.

Definition

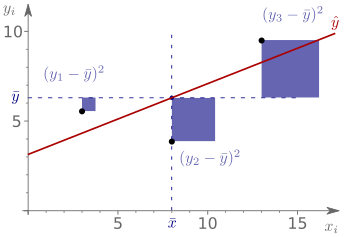
Berechnet wird die totale Quadratsumme durch die Summe der Quadrate der totalen Abweichungen (die Abweichungen der Messwerte von ihrem Mittelwert)

$SQT:=SQ_{\text{Total}}:=\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}$ ,

wobei ${\bar {y}}$ für das arithmetische Mittel steht. Die totale Quadratsumme erfasst die „Gesamtvariation“ in der abhängigen Variablen. Dividiert man die gesamte bzw. totale Quadratsumme durch die Anzahl der Freiheitsgrade (n-1) , erhält man als empirische Varianz die Gesamtvarianz bzw. totale Varianz:

$s_{y}^{2}={\frac {SQT}{n-1}}={\frac {1}{n-1}}\sum _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}$ .

Der Name totale Varianz rührt daher, dass sich die „totale Varianz“ in die „erklärte Varianz“ und die „Restvarianz“ zerlegen lässt.

Zerlegung der totalen Quadratsumme

Diese Animation zeigt die Streuungszerlegung, d.h. die Zerlegung der totalen Quadratsumme in die erklärte Quadratsumme (der Anteil der Gesamtstreuung, der durch ${\hat {y}}$ erklärt werden kann) und die Residuenquadratsumme. Ebenfalls zu sehen ist, dass die –durch die Kleinste-Quadrate-Schätzung gewonnene– Regressionsgerade durch das „Gravitationszentrum“ $G({\overline {x}},{\overline {y}})$ der Punkteverteilung im Streudiagramm verläuft (siehe auch, algebraische Eigenschaften der Kleinste-Quadrate-Schätzer).

Die Quadratsummenzerlegung, auch Zerlegung der Summe der Abweichungsquadrate, Zerlegung der totalen Quadratsumme oder Streuungszerlegung genannt, beschreibt eine Zerlegung der gesamten Abweichungsquadratsumme. Gegeben ein multiples oder einfaches lineares Regressionsmodell mit Achsenabschnitt $y_{i}=\beta _{0}+\beta _{1}x_{i1}+\ldots +\beta _{k}x_{ik}+\varepsilon _{i}$ , welches auf der Stichprobe $(y_{i},x_{i1},\ldots ,x_{ik}),\,i=1,\ldots ,n$ basiert und Beobachtungen umfasst. Die totale Quadratsumme

$SQT=\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}$

lässt sich dann zerlegen in die erklärte Quadratsumme

$SQE=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}$

und die Residuenquadratsumme

$SQR=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}$ :

$\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}+\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}$ ,

was äquivalent ist zu

$SQT=SQE+SQR\quad$ bzw. $\quad SQ_{\text{Total}}=SQ_{\mathrm {Erkl{\ddot {a}}rt} }+SQ_{\text{Rest}}$ .

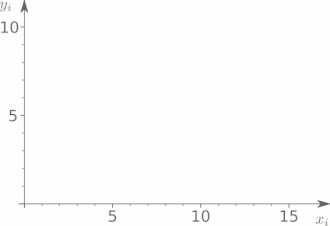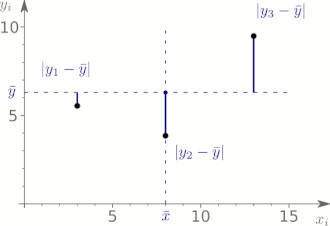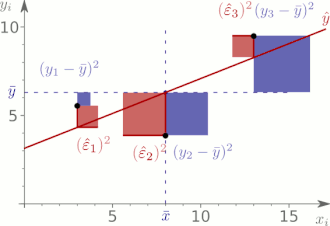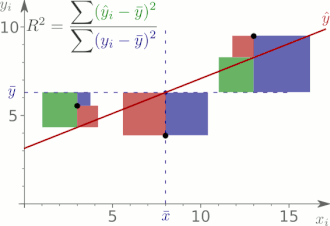
Die Quadratsummenzerlegung bzw. Streuungszerlegung besagt, dass sich die „Gesamtvariation in $\{y_{i}\}$ “ als Summe der „Gesamtvariation in $\{{\hat {y}}_{i}\}$ “ und der „Gesamtvariation in $\{{\hat {\varepsilon }}_{i}\}$ “ ergibt.

Beweis

${\begin{aligned}\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}&=\sum _{i=1}^{n}(y_{i}-{\overline {y}}+{\hat {y}}_{i}-{\hat {y}}_{i})^{2}=\sum _{i=1}^{n}(({\hat {y}}_{i}-{\overline {y}})+\underbrace {(y_{i}-{\hat {y}}_{i})} _{{\hat {\varepsilon }}_{i}})^{2}\\&=\sum _{i=1}^{n}(({\hat {y}}_{i}-{\overline {y}})^{2}+2{\hat {\varepsilon }}_{i}({\hat {y}}_{i}-{\overline {y}})+{\hat {\varepsilon }}_{i}^{2})\\&=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}+\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}+2\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}({\hat {y}}_{i}-{\overline {y}})\\&=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}+\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}+2\underbrace {\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}{\hat {y}}_{i}} _{=0}-2{\overline {y}}\underbrace {\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}} _{=0}\\&=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}+\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}=SQE+SQR\\\end{aligned}}$

wobei die Eigenschaft benutzt wurde, dass die Residuen mit den prognostizierten Werten unkorreliert sind, d.h. $\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}{\hat {y}}_{i}=0$ . Diese Unkorreliertheit der prognostizierten Werte mit den Residuen kann so interpretiert werden, dass in der Prognose bereits alle relevante Information der erklärenden Variablen bezüglich der abhängigen Variablen steckt. Zudem wurde die Eigenschaft verwendet, dass die Summe und damit das arithmetische Mittel der Residuen Null ist (wenn das Modell den Achsenabschnitt enthält) ${\overline {\hat {\varepsilon }}}={\tfrac {1}{n}}\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}=0$ (siehe statistische Eigenschaften der Kleinste-Quadrate-Schätzer). Die Quadratsummenzerlegung kann als „Streuungszerlegung“ interpretiert werden.

Das Verhältnis der erklärten Abweichungsquadratsumme zur gesamten Abweichungsquadratsumme wird Bestimmtheitsmaß genannt. Die Quadratsumme der Residuen wird auch Residuenquadratsumme genannt (oder nicht erklärte Quadratsumme). Verschiedene statistische Analyseverfahren wie etwa die Regressionsanalyse versuchen ein Modell zu finden, das vorhandene Beobachtungswerte besser erklärt als ihr Mittelwert ${\bar {y}}$ .

Basierend auf einem Artikel in:

Wikipedia.de