Residuenquadratsumme

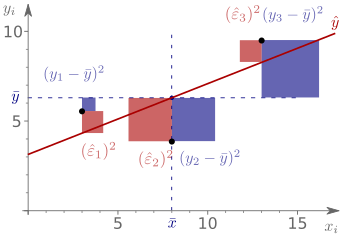
Die Summe der blauen Abweichungsquadrate ist die totale Quadratsumme und die Summe der roten Abweichungsquadrate ist die Residuenquadratsumme.

Die Residuenquadratsumme, Quadratsumme der Residuen, oder auch Summe der Residuenquadrate, bezeichnet in der Statistik die Summe der quadrierten (Kleinste-Quadrate-)Residuen (Abweichungen zwischen Beobachtungswerten und den vorhergesagten Werten) aller Beobachtungen. Da zunächst Abweichungsquadrate (hier Residuenquadrate) gebildet werden und dann über alle Beobachtungen summiert wird, stellt sie eine Abweichungsquadratsumme dar. Die Residuenquadratsumme ist ein Gütekriterium für ein lineares Modell und beschreibt die Ungenauigkeit des Modells. Sie erfasst die Streuung der Beobachtungswerte um die vorhergesagten Werte der Zielgröße, also die Streuung, die durch die Stichproben-Regressionsgerade nicht erklärt werden kann. Sie wird daher auch als die nicht erklärte Abweichungsquadratsumme (oder kurz nicht erklärte Quadratsumme) bezeichnet. Neben der Residuenquadratsumme spielt in der Statistik auch die totale Quadratsumme und die erklärte Quadratsumme eine große Rolle.

Um einen globalen F-Test durchzuführen, sind oft mittlere Abweichungsquadrate von Interesse. Dividiert man die Residuenquadratsumme durch die residualen Freiheitsgrade, erhält man das mittlere Residuenquadrat. Die Teststatistik eines globalen F-Tests ist dann gegeben durch den Quotienten aus dem „mittleren Quadrat der erklärten Abweichungen“ und dem „mittleren Residuenquadrat“.

Abkürzungs- und Bezeichnungsproblematik

Über die genaue Bezeichnung und ihre Abkürzungen gibt es international keine Einigkeit. Die natürliche deutsche Abkürzung für die Residuenquadratsumme bzw. die Summe der (Abweichungs-)Quadrate der Restabweichungen (oder: „Residuen“), ist SAQ_Rest, oder SQR. Die englische Abkürzung SSR ist vieldeutig und führt zu anhaltenden Verwechslungen: Sowohl Sum of Squared Residuals (Residuenquadratsumme) als auch Sum of Squares due to Regression (Regressionsquadratsumme) werden als SSR abgekürzt. Allerdings wird die Regressionsquadratsumme oft auch als erklärte Quadratsumme (Sum of Squares Explained) bezeichnet, deren natürliche englische Abkürzung SSE ist. Die Abkürzungsproblematik wird dadurch verschärft, dass die Residuenquadratsumme oft auch als Fehlerquadratsumme (Sum of Squares Error) bezeichnet wird, deren natürliche englische Abkürzung ebenfalls SSE ist (diese Bezeichnung ist besonders irreführend, da die Fehler und die Residuen unterschiedliche Größen sind). Des Weiteren findet sich für Residuenquadratsumme ebenfalls die englische Abkürzung RSS, statt der Abkürzung SSR, da statt der Bezeichnung Sum of Squared Residuals, oft auch die Bezeichnung Residual Sum of Squares verwendet wird. Auch diese englische Abkürzung kann mit der Regressionsquadratsumme verwechselt werden, die im Englischen auch als Regression Sum of Squares bezeichnet, deren natürliche englische Abkürzung auch hier RSS ist.

Definition

Die Residuenquadratsumme ist definiert durch die Summe der Quadrate der Restabweichungen bzw. Residuen:

$SQR:=SQ_{\text{Rest}}:=\sum _{i=1}^{n}({\hat {\varepsilon }}_{i}-\underbrace {\overline {\hat {\varepsilon }}} _{=0})^{2}=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}=\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}$ .

Die zweite Gleichheit gilt, da ${\overline {\hat {\varepsilon }}}={\frac {1}{n}}\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}=0$ .

Einfache lineare Regression

In der einfachen linearen Regression (Modell mit nur einer erklärenden Variablen) lässt sich die Residuenquadratsumme auch wie folgt ausdrücken:

$SQR=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}=\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}=\sum _{i=1}^{n}(y_{i}-({\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i}))^{2}$

Hierbei stellen die $\varepsilon _{i}=y_{i}-{\hat {y}}_{i}$ die Residuen dar und ${\hat {\beta }}_{0}$ ist die Schätzung des Absolutglieds und ${\hat {\beta }}_{1}$ die Schätzung des Steigungsparameters. Die Methode der kleinsten Quadrate versucht hier die Residuenquadratsumme zu minimieren (vgl. Minimierung der Summe der Fehlerquadrate). Ein spezielleres Konzept ist die PRESS-Statistik, auch prädiktive Residuenquadratsumme (englisch predictive residual sum of squares) genannt.

Es lässt sich zeigen, dass in der einfachen linearen Regression die Residuenquadratsumme wie folgt angegeben werden kann (für einen Beweis, siehe Erklärte Quadratsumme#Einfache lineare Regression)

$SQR=SQT\cdot (1-r_{xy}^{2})$ ,

wobei $SQT$ die totale Quadratsumme und $r_{xy}$ den Bravais-Pearson-Korrelationskoeffizienten darstellt.

Multiple lineare Regression

Die gewöhnlichen Residuen, die durch die Kleinste-Quadrate-Schätzung gewonnen werden, sind in der multiplen linearen Regression gegeben durch

${\hat {\boldsymbol {\varepsilon }}}=\mathbf {y} -{\hat {\mathbf {y} }}=\mathbf {y} -\mathbf {X} \mathbf {b}$ ,

wobei $\mathbf {b} =(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y}$ der Kleinste-Quadrate-Schätzvektor ist. Die Residuenquadratsumme ergibt sich also aus dem Produkt zwischen dem transponierten Residualvektor ${\hat {\boldsymbol {\varepsilon }}}^{\top }$ und dem nicht-transponierten Residualvektor ${\hat {\boldsymbol {\varepsilon }}}$

$SQR=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}={\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}=(\mathbf {y} -\mathbf {X} \mathbf {b} )^{\top }(\mathbf {y} -\mathbf {X} \mathbf {b} )=\sum _{i=1}^{n}(y_{i}-{\hat {\beta }}_{0}-{\hat {\beta }}_{1}x_{i1}-{\hat {\beta }}_{2}x_{i2}-\ldots -{\hat {\beta }}_{k}x_{ik})^{2}$ .

Alternativ lässt sie sich auch schreiben als:

$SQR=\mathbf {y} ^{\top }\mathbf {y} -\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} =\mathbf {y} ^{\top }\mathbf {y} -\mathbf {b} ^{\top }\mathbf {X} ^{\top }{\hat {\mathbf {y} }}$

Die Residuenquadratsumme lässt sich mittels der residuenerzeugenden Matrix auch darstellen als:

$SQR={\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}={\boldsymbol {\varepsilon }}^{\top }(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }){\boldsymbol {\varepsilon }}={\boldsymbol {\varepsilon }}^{\top }\mathbf {Q} {\boldsymbol {\varepsilon }}$ .

Dies zeigt, dass die Residuenquadratsumme eine quadratische Form der theoretischen Störgrößen ist. Eine alternative Darstellung als eine quadratische Form der y-Werte ist

$SQR=\mathbf {y} ^{\top }(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top })\mathbf {y} =\mathbf {y} ^{\top }\mathbf {Q} \mathbf {y}$ .

Rechenbeispiel

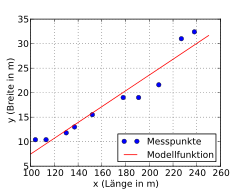
Streudiagramm der Längen und Breiten zehn zufällig ausgewählter Kriegsschiffe.

Folgendes Beispiel soll die Berechnung der Residuenquadratsumme zeigen. Es wurden zufällig zehn Kriegsschiffe ausgewählt und bezüglich ihrer Länge und Breite (in Metern) analysiert. Es soll untersucht werden, ob die Breite eines Kriegsschiffs möglicherweise in einem festen Bezug zur Länge steht.

Das Streudiagramm lässt einen linearen Zusammenhang zwischen Länge und Breite eines Schiffs vermuten. Eine mittels der Kleinste-Quadrate-Schätzung durchgeführte einfache lineare Regression ergibt für das Absolutglied ${\hat {\beta }}_{0}=-8{,}6450715$ und die Steigung ${\hat {\beta }}_{1}=0{,}1612340$ (für die Berechnung der Regressionsparameter siehe Beispiel mit einer Ausgleichsgeraden). Die geschätzte Regressionsgerade lautet somit

${\widehat {\mathtt {breite}}}=-8{,}6450715+0{,}1612340\cdot {\mathtt {l{\ddot {a}}nge}}$ .

Die Gleichung stellt die geschätzte Breite ${\hat {y}}={\widehat {\mathtt {breite}}}$ als Funktion der Länge $x={\mathtt {l{\ddot {a}}nge}}$ dar. Die Funktion zeigt, dass die Breite der ausgewählten Kriegsschiffe grob einem Sechstel ihrer Länge entspricht.

Kriegsschiff	Länge (m)	Breite (m)	$y_{i}^{*}$	$y_{i}^{}\cdot y_{i}^{}$	${\hat {y}}_{i}$	${\hat {\varepsilon }}_{i}$	${\hat {\varepsilon }}_{i}^{2}$
	$x_{i}$	$y_{i}$	$y_{i}-{\overline {y}}$	$(y_{i}-{\overline {y}})^{2}$	${\hat {y}}(x_{i})$	$y_{i}-{\hat {y}}_{i}$	$(y_{i}-{\hat {y}}_{i})^{2}$
1	208	21,6	3,19	10,1761	24,8916	−3,2916	10,8347
2	152	15,5	−2,91	8,4681	15,8625	−0,3625	0,1314
3	113	10,4	−8,01	64,1601	9,5744	0,8256	0,6817
4	227	31,0	12,59	158,5081	27,9550	3,045	9,2720
5	137	13,0	−5,41	29,2681	13,4440	−0,4440	0,1971
6	238	32,4	13,99	195,7201	29,7286	2,6714	7,1362
7	178	19,0	0,59	0,3481	20,0546	−1,0546	1,1122
8	104	10,4	−8,01	64,1601	8,1233	2,2767	5,1835
9	191	19,0	0,59	0,3481	22,1506	−3,1506	9,9265
10	130	11,8	−6,61	43,6921	12,3154	−0,5154	0,2656
Σ	1678	184,1		574,8490		0,0000	44,7405
Σ/n	167,8	18,41		57,48490		0,0000	4,47405

Aus der Tabelle lässt neben der totalen Quadratsumme der Messwerte $574{,}849\;{\text{m}}^{2}$ auch die Residuenquadratsumme (letzte Spalte) $44{,}7405\;{\text{m}}^{2}$ ablesen. Auf diesen beiden Größen aufbauend lässt sich ebenfalls das Bestimmtheitsmaß berechnen (siehe auch Bestimmtheitsmaß#Rechenbeispiel).

Eigenschaften der Residuenquadratsumme

Verteilung der Residuenquadratsumme

Wenn die Beobachtungen mehrdimensional normalverteilt sind, dann gilt für den Quotienten aus der Residuenquadratsumme $SQR$ und der Störgrößenvarianz $\sigma ^{2}$ , dass er einer Chi-Quadrat-Verteilung mit n-p (mit $p=k+1$ ) Freiheitsgraden folgt:

${\frac {SQR}{\sigma ^{2}}}={\frac {{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}}{\sigma ^{2}}}=(n-p){\frac {{\hat {\sigma }}^{2}}{\sigma ^{2}}}\sim \chi ^{2}(n-p)$ ,

wobei ${\hat {\sigma }}^{2}$ die erwartungstreue Schätzung der Varianz der Störgrößen darstellt.

Erwartungswert der Residuenquadratsumme

Man kann zeigen, dass der Erwartungswert der Residuenquadratsumme $\sigma ^{2}(n-k-1)$ ergibt

$\operatorname {E} ({\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}})=\operatorname {E} ({\boldsymbol {\varepsilon }}^{\top }(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }){\boldsymbol {\varepsilon }})=\sigma ^{2}(n-k-1)$ ,

wobei $(n-k-1)$ die Anzahl der Freiheitsgrade der Residuenquadratsumme und $\sigma ^{2}$ die Störgrößenvarianz ist. Daraus lässt sich schließen, dass der erwartungstreue Schätzer für die unbekannte skalare Störgrößenvarianz gegeben sein muss durch ${\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}/(n-k-1)$ .

Mittleres Residuenquadrat

Wenn man die Residuenquadratsumme durch die Anzahl der Freiheitsgrade dividiert, dann erhält man als mittleres Abweichungsquadrat das „mittlere Residuenquadrat“ (Mittleres Quadrat der Residuen, kurz: MQR)

$MQR={\frac {\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{n-k-1}}={\frac {SQR}{n-k-1}}$ .

Die Quadratwurzel des mittleren Residuenquadrats ist der Standardfehler der Regression. In der linearen Einfachregression, die den Zusammenhang zwischen der Einfluss- und der Zielgröße mithilfe von zwei Regressionsparametern herstellt ist das mittlere Residuenquadrat gegeben durch

$MQR={\frac {\sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{n-2}}={\frac {SQR}{n-2}}$ .

Gewichtete Residuenquadratsumme

In der verallgemeinerten Kleinste-Quadrate-Schätzung und anderen Anwendungen wird oft eine gewichtete Version der Residuenquadratsumme verwendet

$GSQR=\sum _{i=1}^{n}{\frac {1}{w_{i}}}(y_{i}-\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }})^{2}=(\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})^{\top }\,\mathbf {W} ^{-1}(\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})\quad {\text{mit}}\quad \mathbf {W} =\operatorname {diag} (w_{1},\ldots ,w_{n})$ ,

wobei $\mathbf {W} =\operatorname {diag} (w_{1},\ldots ,w_{n})$ die Gewichtsmatrix darstellt.

Penalisierte Residuenquadratsumme

Im Kontext von penalisierten Splines (kurz: P-Splines) wird eine sogenannte penalisierte Residuenquadratsumme verwendet, die approximativ der gewöhnlichen Residuenquadratsumme entspricht.

Basierend auf einem Artikel in:

Wikipedia.de