Multiple lineare Regression
In der Statistik ist die multiple lineare Regression, auch mehrfache lineare Regression (kurz: MLR) oder lineare Mehrfachregression genannt, ein regressionsanalytisches Verfahren und ein Spezialfall der linearen Regression. Die multiple lineare Regression ist ein statistisches Verfahren, mit dem versucht wird, eine beobachtete abhängige Variable durch mehrere unabhängige Variablen zu erklären. Das dazu verwendete Modell ist linear in den Parametern, wobei die abhängige Variable eine Funktion der unabhängigen Variablen ist. Diese Beziehung wird durch eine additive Störgröße überlagert. Die multiple lineare Regression stellt eine Verallgemeinerung der einfachen linearen Regression bzgl. der Anzahl der Regressoren dar.
Das klassische Modell der linearen Mehrfachregression
Im Folgenden wird von linearen Funktionen ausgegangen. Es ist dann keine
weitere Beschränkung der Allgemeinheit, dass diese Funktionen direkt aus den
unabhängigen (erklärenden, exogenen) Variablen bestehen und es ebenso viele zu
schätzende Regressionsparameter
gibt wie unabhängige Variablen
(Index
).
Zum Vergleich: In der einfachen linearen Regression ist
und
konstant gleich
,
der zugehörige Regressionsparameter also der Achsenabschnitt.
Das Modell für
Messungen der abhängigen (endogenen) Variablen
ist also
,
mit Störgrößen
,
die rein zufällig
sind, falls das lineare
Modell passt. Für das Modell wird weiterhin angenommen, dass die Gauß-Markow-Annahmen
gelten. In einem stichprobentheoretischen Ansatz wird jedes Stichprobenelement
als eine eigene Zufallsvariable
interpretiert, ebenso jedes
.
Liegen die Daten
vor, so ergibt sich folgendes lineare Gleichungssystem:
Das multiple lineare Regressionsmodell (selten und doppeldeutig allgemeines lineares Modell) lässt sich in Matrixschreibweise wie folgt formulieren
Dies ist das zugrundeliegende Modell in der Grundgesamtheit und
wird auch als „wahres
Modell“ bezeichnet. Hierbei stehen ,
und
für die Vektoren bzw. Matrizen:
und
und
eine
-Matrix
(Versuchsplan- oder Datenmatrix):
, wobei
Aufgrund der unterschiedlichen Schreibweisen für
lässt sich erkennen, dass sich das Modell
auch darstellen lässt als:
mit
,
hierbei ist
die beobachtete abhängige Variable für Beobachtung
und
,
sind die unabhängigen Variablen. Wie gewöhnlich ist,
das Absolutglied und
sind unbekannte skalare
Steigungsparameter. Die Störgröße
für Beobachtung
ist eine unbeobachtbare Zufallsvariable. Der Vektor
ist der transponierte
Vektor der Regressoren
und
wird auch als linearer
Prädiktor bezeichnet.
Die wesentliche Voraussetzung an das multiple lineare Regressionsmodell ist,
dass es bis auf die Störgröße
das „wahre Modell“ beschreibt.
Dabei wird in der Regel nicht genau spezifiziert, von welcher Art die Störgröße
ist; sie kann beispielsweise von zusätzlichen Faktoren oder Messfehlern
herrühren. Jedoch nimmt man als Grundvoraussetzung an, dass dessen
Erwartungswert (in allen Komponenten) 0 ist:
(Annahme 1). Diese Annahme bedeutet, dass das Modell grundsätzlich für korrekt
gehalten wird und die beobachtete Abweichung als zufällig angesehen wird oder
von vernachlässigbaren äußeren Einflüssen herrührt. Typisch ist die Annahme,
dass die Komponenten des Vektors unkorreliert
sind (Annahme 2) und dieselbe Varianz
besitzen (Annahme 3), wodurch sich mit Hilfe klassischer Verfahren wie der Methode
der kleinsten Quadrate (englisch
ordinary least squares, kurz: OLS) einfache Schätzer für die
unbekannten Parameter
und
ergeben. Die Methode wird daher auch (multiple lineare) KQ-Regression
(englisch
OLS regression) genannt.
Zusammenfassend wird für die Störgrößen angenommen, dass
- (A1) sie den Erwartungswert null haben:
,
- (A2) unkorreliert sind:
und
- (A3) eine homogene
Varianz haben:
(skalare Kovarianzmatrix).
Hierbei bezeichnet
den Nullvektor und
die Einheitsmatrix
der Dimension
.
Die oben genannten Annahmen sind die Annahmen der klassischen
linearen Regression. Das Modell (die Gleichung
zusammen mit obigen Annahmen) wird daher das klassische Modell der linearen
Mehrfachregression genannt.
Statt nur die Varianzen und Kovarianzen der Störgrößen einzeln zu betrachten, werden diese in folgender Kovarianzmatrix zusammengefasst:
Somit gilt für
mit
.
Über diese grundlegende Annahme hinaus sind grundsätzlich alle
Verteilungsannahmen an
erlaubt. Wird zudem vorausgesetzt, dass der Vektor
mehrdimensional
normalverteilt ist, lässt sich ferner zeigen, dass die beiden Schätzer
Lösungen der Maximum-Likelihood-Gleichungen
sind (siehe Statistische
Inferenz). In diesem Modell ist die Unabhängigkeit der Störgrößen dann
gleichbedeutend mit der der
.
Schätzung des Parametervektors mit der Kleinste-Quadrate-Schätzung
Auch im multiplen linearen Regressionsmodell wird der Vektor der Störgrößen
mithilfe der Kleinste-Quadrate-Schätzung
(KQ-Schätzung) minimiert, das heißt, es soll
so gewählt werden, dass die euklidische
Norm
minimal wird. Im Folgenden wird der Ansatz benutzt,
dass die Residuenquadratsumme
minimiert wird. Dazu wird vorausgesetzt, dass
den Rang
hat. Dann ist
invertierbar und man
erhält als Minimierungsproblem:
Die Bedingung erster Ordnung (Nullsetzen des Gradienten) lautet:
Die partiellen Ableitungen erster Ordnung lauten:
Dies zeigt, dass sich die Bedingung erster Ordnung für den Vektor
der geschätzten Regressionsparameter kompakt darstellen lässt als:
bzw.
.
Dieses lineare Gleichungssystem wird in der Regel (Gaußsches) Normalgleichungssystem genannt.
Da die Matrix
den Rang
hat, ist die quadratische
symmetrische
Matrix
nichtsingulär
und die Inverse für
existiert. Daher erhält man nach linksseitiger
Multiplikation mit der Inversen der Produktsummenmatrix
als Lösung des Minimierungsproblems den folgenden Vektor der geschätzten
Regressionskoeffizienten:
Wenn der Rang von
kleiner als
ist, dann ist
nicht invertierbar, also das Normalgleichungssystem nicht eindeutig lösbar,
mithin
nicht identifizierbar,
siehe hierzu aber den Begriff der Schätzbarkeit.
Da
die Residuenquadratsumme
minimiert, wird
auch Kleinste-Quadrate-Schätzer (kurz: KQ-Schätzer) genannt.
Alternativ kann der Kleinste-Quadrate-Schätzer durch Einsetzen des wahren
Modells
auch dargestellt werden als
Für die Kovarianzmatrix des Kleinste-Quadrate-Schätzers ergibt sich (dargestellt in kompakter Form):[5]
Im Fall der linearen Einfachregression ()
reduziert sich die obigen Formel auf die bekannten Ausdrücke für die Varianzen
der KQ-Schätzer
und
(siehe Statistische
Eigenschaften der Kleinste-Quadrate-Schätzer).
| Beweis |
|
|
Man erhält mit Hilfe des Kleinste-Quadrate-Schätzers
das Gleichungssystem
,
wobei
der Vektor der Residuen
und
die Schätzung für
ist. Das Interesse der Analyse liegt oft in der Schätzung
oder in der Vorhersage der abhängigen Variablen
für ein gegebenes Tupel von
.
Diese berechnet sich als
.
Güteeigenschaften des Kleinste-Quadrate-Schätzers
Erwartungstreue
Im multiplen Fall kann man genauso wie im einfachen
Fall zeigen, dass der Kleinste-Quadrate-Schätzvektor erwartungstreu für
ist. Dies gilt allerdings nur, wenn die Annahme der
Exogenität
der Regressoren gegeben ist. Dies ist der Fall, wenn die möglicherweise
zufälligen Regressoren und die Störgrößen unkorreliert sind, d.h. wenn
gilt. Wenn man also hier voraussetzt, dass die exogenen Variablen keine
Zufallsvariablen sind, sondern wie in einem Experiment kontrolliert
werden können, gilt
bzw.
und damit ist
erwartungstreu für
.
| Beweis |
|
|
Falls die Exogenitätsannahme nicht zutrifft, ,
ist der Kleinste-Quadrate-Schätzer nicht erwartungstreu. Es liegt also eine
Verzerrung
(englisch
bias) vor, d.h., „im Mittel“ weicht der Parameterschätzer vom
wahren Parameter ab:
.
Der Erwartungswert
des Kleinste-Quadrate-Parametervektor für
ist also nicht gleich dem wahren Parameter
,
siehe dazu auch unter Regression
mit stochastischen Regressoren.
Effizienz
Der Kleinste-Quadrate-Schätzer ist linear:
.
Nach dem Satz
von Gauß-Markow ist der Schätzer ,
bester
linearer erwartungstreuer Schätzer (BLES bzw. englisch Best
Linear Unbiased Estimator, kurz: BLUE), das heißt, er ist derjenige
lineare
erwartungstreue Schätzer, der unter allen linearen erwartungstreuen Schätzern
die kleinste Varianz bzw. Kovarianzmatrix besitzt. Für diese Eigenschaften der
Schätzfunktion
braucht keine Verteilungsinformation der Störgröße vorzuliegen. Wenn die
Störgrößen normalverteilt
sind, ist
Maximum-Likelihood-Schätzer
und nach dem Satz
von Lehmann-Scheffé beste erwartungstreue Schätzung (BES bzw. englisch Best
Unbiased Estimator, kurz: BUE).
Konsistenz
Der KQ-Schätzer ist unter den bisherigen Annahmen erwartungstreu für
(
),
wobei die Stichprobengröße
keinen Einfluss auf die Erwartungstreue
hat (schwaches
Gesetz der großen Zahlen). Ein Schätzer ist genau dann konsistent
für den wahren Wert, wenn er in Wahrscheinlichkeit
gegen den wahren Wert konvergiert
(englisch
probability limit, kurz: plim). Die Eigenschaft der Konsistenz
bezieht also das Verhalten des Schätzers mit ein, wenn die Anzahl der
Beobachtungen größer wird.
Für die Folge
gilt, dass sie in Wahrscheinlichkeit gegen den wahren Parameterwert
konvergiert
oder vereinfacht ausgedrückt
bzw.
Die Grundlegende Annahme, um die Konsistenz des KQ-Schätzers sicherzustellen lautet
,
d.h. man geht davon aus, dass das durchschnittliche Quadrat der beobachteten Werte der erklärenden Variablen auch bei einem ins Unendliche gehendem Stichprobenumfang endlich bleibt (siehe Produktsummenmatrix). Außerdem nimmt man an, dass
.
Die Konsistenz kann wie folgt gezeigt werden:
| Beweis |
|
|
Hierbei wurde das Slutsky-Theorem und die Eigenschaft verwendet, dass wenn
deterministisch bzw. nichtstochastisch ist
gilt.
Folglich ist der Kleinste-Quadrate-Schätzer konsistent für .
Die Eigenschaft besagt, dass mit steigender Stichprobengröße die
Wahrscheinlichkeit, dass der Schätzer
vom wahren Parameter
abweicht, sinkt. Weiterhin lässt sich durch das Chintschin-Theorem
zeigen, dass für die durch die KQ-Schätzung gewonnene Störgrößenvarianz gilt,
dass sie konsistent für
ist, d. h.
.
| Beweis |
|
Dazu schreibt man zunächst die geschätzte Störgrößenvarianz wie folgt um Damit ergibt sich als Wahrscheinlichkeitslimes Somit ist |
Verbindung zur optimalen Versuchsplanung
Wenn die Werte der unabhängigen Variablen
einstellbar sind, kann durch optimale Wahl dieser Werte die Matrix
(d.h. bis auf einen Faktor die Kovarianzmatrix
des Kleinste-Quadrate-Schätzers) im Sinne der Loewner-Halbordnung
„verkleinert“ werden. Das ist eine Hauptaufgabe der optimalen
Versuchsplanung.
Residuen und geschätzte Zielwerte
Die Schätzwerte der
berechnen sich mithilfe des KQ-Schätzers
als
,
wobei man dies auch kürzer als
mit
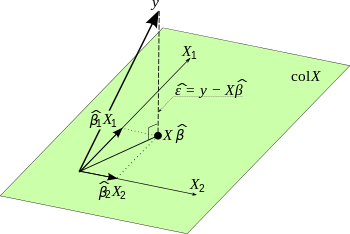
schreiben kann. Die Projektionsmatrix
ist die Matrix der Orthogonalprojektion
auf den Spaltenraum von
und hat maximal den Rang
.
Sie wird auch Prädiktionsmatrix
genannt, da sie die vorhergesagten Werte (
-Werte)
generiert wenn man die Matrix auf die
-Werte
anwendet. Die Prädiktionsmatrix beschreibt numerisch die Projektion von
auf die durch
definierte Ebene.
Der Residualvektor lässt sich mittels der Prädiktionsmatrix darstellen als:
.
Die Matrix
wird auch als Residualmatrix
bezeichnet und mit
abgekürzt. Ferner ist die Residuenquadratsumme als nichtlineare Transformation
Chi-Quadrat-verteilt
mit
Freiheitsgraden.
Dies zeigt folgende Beweisskizze:
| Beweisskizze |
|
Sei
damit erhält man
wobei und der Satz von Cochran verwendet wurden. |
Außerdem gilt ebenso
.
Erwartungstreue Schätzung des unbekannten Varianzparameters
Obwohl manchmal angenommen wird, dass die Störgrößenvarianz
bekannt ist, muss man davon ausgehen, dass sie in den meisten Anwendungsfällen
unbekannt ist (beispielsweise bei der Schätzung von Nachfrageparametern in
ökonomischen Modellen, oder Produktionsfunktionen).
Ein naheliegender Schätzer des Vektors der Störgrößen
ist der Residulavektor
,
der aus der Regression gewonnen wird. Die in den Residuen steckende Information
könnte also für einen Schätzer der Störgrößenvarianz genutzt werden. Aufgrund
der Tatsache, dass
gilt, ist
aus frequentistischer
Sicht der „Mittelwert“ von
.
Die Größe
ist aber unbeobachtbar, da die Störgrößen unbeobachtbar sind. Wenn man statt
nun das beobachtbare Pendant
benutzt, führt dies zum Schätzer:
,
wobei
die Residuenquadratsumme
darstellt. Allerdings erfüllt der Schätzer nicht gängige Qualitätskriterien
für Punktschätzer und wird daher nicht oft genutzt.
Beispielsweise ist der Schätzer nicht erwartungstreu für
.
Dies liegt daran, dass der Erwartungswert
der Residuenquadratsumme
ergibt und daher für den Erwartungswert dieses Schätzers
gilt.
Eine erwartungstreue Schätzung für
,
d.h. eine Schätzung die
erfüllt, ist in der multiplen linearen Regression gegeben ist durch das mittlere
Residuenquadrat
mit dem Kleinste-Quadrate-Schätzer
.
Wenn nun bei der Kovarianzmatrix des KQ-Schätzvektors
durch
ersetzt wird ergibt sich für die geschätzte Kovarianzmatrix des KQ-Schätzers
.
Statistische Inferenz
Für die statistische Inferenz (Schätzen und Testen) wird noch die Information
über die Verteilung des Vektors der Störgrößen
gefordert. Bedingt auf die Datenmatrix
sind die
unabhängig und identisch verteilt und folgen einer
-Verteilung.
Äquivalent ist
(bedingt auf
)
mehrdimensional
normalverteilt mit dem Erwartungswert
und der Kovarianzmatrix
,
d.h.
Hier sind stochastisch
unabhängige Zufallsvariablen auch unkorreliert. Weil der Störgrößenvektor
mehrdimensional normalverteilt ist folgt daraus, dass auch der Regressand
mehrdimensional normalverteilt ist ().
Aufgrund der Tatsache, dass beim KQ-Schätzer die einzige zufällige Komponente
ist, folgt für den Parametervektor
,
dass er ebenfalls normalverteilt ist:
.
Multiples Bestimmtheitsmaß
Das Bestimmtheitsmaß
ist eine Maßzahl für die Güte (Bestimmtheit) einer multiplen linearen
Regression. In der multiplen linearen Regression, lässt sich das Bestimmtheitsmaß
darstellen als
.
oder
.
Die Besonderheit beim multiplen Bestimmtheitsmaß ist, dass es nicht wie in
der einfachen linearen Regression dem quadrierten Korrelationskoeffizienten
zwischen
und
,
sondern dem Quadrat des Korrelationskoeffizienten zwischen den Messwerten
und den Schätzwerten
entspricht (für einen Beweis, siehe Matrixschreibweise).
Test auf Gesamtsignifikanz eines Modells
Hat man eine Regression ermittelt, ist man auch an der Güte dieser Regression
interessiert. Im Fall
für alle
wird häufig als Maß für die Güte das Bestimmtheitsmaß
verwendet. Generell gilt, je näher der Wert des Bestimmtheitsmaßes bei
liegt, desto besser ist die Güte der Regression. Ist das Bestimmtheitsmaß klein,
kann man seine Signifikanz
durch das Hypothesenpaar
gegen
,
mit der Prüfgröße
testen. Die Prüfgröße
ist F-verteilt mit
und
Freiheitsgraden. Überschreitet die Prüfgröße bei einem Signifikanzniveau
den kritischen Wert
,
das
-Quantil
der F-Verteilung mit
und
Freiheitsgraden, wird
abgelehnt.
ist dann ausreichend groß, mindestens ein Regressor trägt also vermutlich
genügend viel Information zur Erklärung von
bei.
Unter den Voraussetzungen des klassischen
linearen Regressionsmodells ist der Test ein Spezialfall der einfachen
Varianzanalyse. Für jeden Beobachtungswert
ist die Störgröße
und damit
-verteilt
(mit
der wahre Regressionswert in der Grundgesamtheit), d.h., die
Voraussetzungen der Varianzanalyse sind erfüllt. Sind alle
-Koeffizienten
gleich null, so ist dies äquivalent zur Nullhypothese der Varianzanalyse:
.
Die Residualanalyse, bei der man die Residuen über den unabhängigen Variablen aufträgt, gibt Aufschluss über
- die Richtigkeit des angenommenen linearen Zusammenhangs,
- mögliche Ausreißer,
- Homoskedastizität, Heteroskedastizität.
Ein Ziel bei der Residualanalyse ist es, die Voraussetzung der
Residuen
zu überprüfen. Hierbei ist es wichtig zu beachten, dass
gilt. Das Residuum
ist mit der Formel
berechenbar. Im Gegensatz hierzu ist die Störgröße
nicht berechenbar oder beobachtbar. Nach den oben getroffenen Annahmen soll für
alle Störgrößen gelten
Es liegt somit eine Varianzhomogenität
vor. Dieses Phänomen wird auch als Homoskedastizität
bezeichnet und ist auf die Residuen übertragbar. Dies bedeutet: Wenn man die
unabhängigen Variablen
gegen die Residuen
aufträgt, sollten keine systematischen Muster erkennbar sein.
-
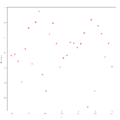 Beispiel 1 zur Residualanalyse
Beispiel 1 zur Residualanalyse -
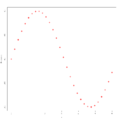 Beispiel 2 zur Residualanalyse
Beispiel 2 zur Residualanalyse -
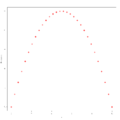 Beispiel 3 zur Residualanalyse
Beispiel 3 zur Residualanalyse
In den obigen drei Grafiken wurden die unabhängigen Variablen
gegen die Residuen
abgetragen, und im Beispiel 1 sieht man, dass hier tatsächlich kein
erkennbares Muster in den Residuen vorliegt, d.h., dass die Annahme der
Varianzhomogenität erfüllt ist. In den Beispielen 2 und 3 dagegen ist diese
Annahme nicht erfüllt: Man erkennt ein Muster. Zur Anwendung der linearen
Regression sind daher hier zunächst geeignete Transformationen
durchzuführen. So ist im Beispiel 2 ein Muster zu erkennen, das an eine Sinus-Funktion erinnert, womit
hier eine Daten-Transformation der Form
denkbar wäre, während im Beispiel 3 ein Muster zu erkennen ist, das an eine
Parabel erinnert, in diesem Fall also eine Daten-Transformation der Form
angebracht sein könnte.
Beitrag der einzelnen Regressoren zur Erklärung der abhängigen Variablen
Man ist daran interessiert, ob man einzelne Parameter oder Regressoren aus
dem Regressionsmodell entfernen kann, ob also ein Regressor nicht (oder nur
gering) zur Erklärung von
beiträgt. Dies ist dann möglich, falls ein Parameter
gleich null ist, somit testet man die Nullhypothese
.
Das heißt, man testet, ob der
-te
Parameter gleich Null ist. Wenn dies der Fall ist, kann der zugehörige
-te
Regressor
aus dem Modell entfernt werden. Der Vektor
ist als lineare Transformation von
wie folgt verteilt:
Wenn man die Varianz der Störgrößen schätzt, erhält man für die geschätzte Kovarianzmatrix des Kleinste-Quadrate-Schätzers
.
Die geschätzte Varianz
eines Regressionsparameters
steht als
-tes
Diagonalelement in der geschätzten Kovarianzmatrix. Es ergibt sich die Prüfgröße
,
wobei die Wurzel der geschätzten Varianz
des
-ten
Parameters den (geschätzten) Standardfehler
des Regressionskoeffizienten
darstellt.
Die Prüf- bzw. Pivotstatistik
ist t-verteilt
mit
Freiheitsgraden. Ist
größer als der kritische Wert
,
dem
-Quantil
der
-Verteilung
mit
Freiheitsgraden, wird die Hypothese abgelehnt. Somit wird der Regressor
im Modell beibehalten und der Beitrag des Regressors
zur Erklärung von
ist signifikant groß, d.h. signifikant von null verschieden.
Vorhersage
Ein einfaches Modell zur Vorhersage von endogenen Variablen ergibt sich durch
,
wobei
den Vektor von zukünftigen abhängigen Variablen und
die Matrix der erklärenden Variablen zum Zeitpunkt
darstellt.
Die Vorhersage wird wie folgt dargestellt: ,
woraus sich folgender Vorhersagefehler
ergibt:
Eigenschaften des Vorhersagefehlers:
Der Vorhersagefehler
ist im Mittel null:
Die Kovarianzmatrix des Vorhersagefehlers lautet:
Ermittelt man einen Vorhersagewert, möchte man möglicherweise wissen, in
welchem Intervall sich die vorhergesagten Werte mit einer festgelegten
Wahrscheinlichkeit bewegen. Man wird also ein Vorhersageintervall
für den durchschnittlichen Vorhersagewert
ermitteln. Im Fall der linearen Einfachregression ergibt sich für die Varianz
des Vorhersagefehlers
.
Man erhält dann als Vorhersageintervall
für die Varianz des Vorhersagefehlers
.
Speziell für den Fall der einfachen linearen Regression ergibt sich das Vorhersageintervall:
Aus dieser Form des Vorhersageintervalls erkennt man sofort, dass das
Vorhersageintervall breiter wird, wenn sich die exogene Vorhersagevariable
vom „Gravitationszentrum“ der Daten entfernt. Schätzungen der endogenen
Variablen sollten also im Beobachtungsraum der Daten liegen, sonst werden sie
sehr unzuverlässig.
Das verallgemeinerte Modell der linearen Mehrfachregression
Beim verallgemeinerten
Modell der linearen Mehrfachregression wird für die Strukturbeziehung
zugelassen, dass die Störgrößen heteroskedastisch und autokorreliert sind. Die
Kovarianzmatrix des Störgrößenvektors ist dann nicht wie gewöhnlich unter den
Gauß-Markow-Annahmen
,
sondern hat die Struktur
,
wobei
als eine beliebige bekannte reelle nichtsinguläre positiv
definite
Matrix angenommen wird und
ein noch unbekannter Skalar darstellt. Das resultierende Modell
mit
nennt man verallgemeinertes (multiples) lineares
Regressionsmodell (mit fixen Regressoren), kurz VLR.
Polynomiale Regression
Die polynomiale Regression ist ein Spezialfall der multiplen linearen
Regression. Das multiple lineare Regressionsmodell wird auch zur Lösung von
speziellen (im Hinblick auf die erklärenden Variablen) nichtlinearen
Regressionsproblemen herangezogen. Bei der polynomialen Regression wird der
Erwartungswert der abhängigen Variablen von den erklärenden Variablen mithilfe
eines Polynoms vom Grade ,
also durch die Funktionsgleichung
beschrieben. Man erhält ein multiples lineares Regressionsmodell mit der oben
genannten Regressionsfunktion, wenn man für die Potenzen von
die Bezeichnungen
einführt. Im Falle
spricht man von quadratischer Regression.
Beispiel
Zur Illustration der multiplen Regression wird im folgenden Beispiel
untersucht, wie die abhängige Variable :
Bruttowertschöpfung
(in Preisen von 95; bereinigt, Mrd. Euro) von den unabhängigen Variablen
„Bruttowertschöpfung nach Wirtschaftsbereichen Deutschland (in jeweiligen
Preisen; Mrd. EUR)“ abhängt. Da man in der Regel die Berechnung eines
Regressionsmodells am Computer durchführt, wird in diesem Beispiel exemplarisch
dargestellt, wie eine multiple Regression mit der Statistik-Software
R durchgeführt werden kann.
| Variable | Beschreibung der Variablen |
|---|---|
| Bruttowertschöpfung in Preisen von 95 (bereinigt) | |
| Bruttowertschöpfung von Land- und Forstwirtschaft, Fischerei | |
| Bruttowertschöpfung des produzierenden Gewerbes ohne Baugewerbe | |
| Bruttowertschöpfung im Baugewerbe | |
| Bruttowertschöpfung von Handel, Gastgewerbe und Verkehr | |
| Bruttowertschöpfung durch Finanzierung, Vermietung und Unternehmensdienstleister | |
| Bruttowertschöpfung von öffentlichen und privaten Dienstleistern |
Zunächst lässt man sich ein Streudiagramm ausgeben. Es zeigt, dass die gesamte Wertschöpfung offensichtlich mit den Wertschöpfungen der wirtschaftlichen Bereiche positiv korreliert ist. Das erkennt man daran, dass die Datenpunkte in der ersten Spalte der Grafik in etwa auf einer Geraden mit einer positiven Steigung liegen. Auffällig ist, dass die Wertschöpfung im Baugewerbe negativ mit den anderen Sektoren korreliert. Dies erkennt man daran, dass in der vierten Spalte die Datenpunkte näherungsweise auf einer Geraden mit einer negativen Steigung liegen.
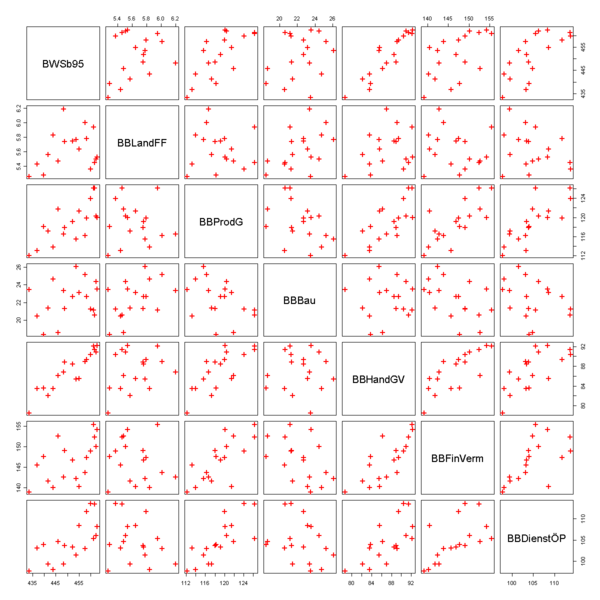
In einem ersten Schritt gibt man das Modell mit allen Regressoren in R ein:
lm(BWSb95~BBLandFF+BBProdG+BBBau+BBHandGV+BBFinVerm+BBDienstÖP)
Anschließend lässt man sich in R ein Summary des Modells mit allen Regressoren ausgeben, dann erhält man folgende Auflistung:
Residuals:
Min 1Q Median 3Q Max
−1.5465 −0.8342 −0.1684 0.5747 1.5564
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 145.6533 30.1373 4.833 0.000525 ***
BBLandFF 0.4952 2.4182 0.205 0.841493
BBProdG 0.9315 0.1525 6.107 7.67e−05 ***
BBBau 2.1671 0.2961 7.319 1.51e−05 ***
BBHandGV 0.9697 0.3889 2.494 0.029840 *
BBFinVerm 0.1118 0.2186 0.512 0.619045
BBDienstÖP 0.4053 0.1687 2.402 0.035086 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.222 on 11 degrees of freedom
Multiple R-Squared: 0.9889, Adjusted R-squared: 0.9828
F-statistic: 162.9 on 6 and 11 DF, p-value: 4.306e−10
Der globale
F-Test ergibt eine Prüfgröße von .
Diese Prüfgröße hat einen p-Wert
von
,
somit ist die Anpassung signifikant gut.
Die Analyse der einzelnen Beiträge der Variablen (Tabelle
Coefficients) des Regressionsmodells ergibt bei einem Signifikanzniveau von
,
dass die Variablen
und
offensichtlich die Variable
nur unzureichend erklären können. Dies erkennt man daran, dass die zugehörigen
-Werte
zu diesen beiden Variablen verhältnismäßig klein sind, und somit die Hypothese,
dass die Koeffizienten dieser Variablen null sind, nicht verworfen werden kann.
Die Variablen
und
sind gerade noch signifikant. Besonders stark korreliert ist
(in diesem Beispiel also
)
mit den Variablen
und
,
was man an den zugehörigen hohen
-Werten
erkennen kann.
Im nächsten Schritt werden die nicht-signifikanten Regressoren
und
aus dem Modell entfernt:
lm(BWSb95~BBProdG+BBBau+BBHandGV+BBDienstÖP)
Anschließend lässt man sich wiederum ein Summary des Modells ausgeben, dann erhält man folgende Auflistung:
Residuals:
Min 1Q Median 3Q Max
−1.34447 −0.96533 −0.05579 0.82701 1.42914
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 158.00900 10.87649 14.528 2.05e−09 ***
BBProdG 0.93203 0.14115 6.603 1.71e−05 ***
BBBau 2.03613 0.16513 12.330 1.51e−08 ***
BBHandGV 1.13213 0.13256 8.540 1.09e−06 ***
BBDienstÖP 0.36285 0.09543 3.802 0.0022 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.14 on 13 degrees of freedom
Multiple R-Squared: 0.9886, Adjusted R-squared: 0.985
F-statistic: 280.8 on 4 and 13 DF, p-value: 1.783e−12
Dieses Modell liefert eine Prüfgröße von .
Diese Prüfgröße hat einen p-Wert
von
,
somit ist die Anpassung besser als im ersten Modell. Dies ist vor allem darauf
zurückzuführen, dass in dem jetzigen Modell alle Regressoren signifikant sind.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.07. 2025