Optimierungsproblem

Ein Optimierungsproblem ist ein mathematisches Problem. Die Aufgabe besteht darin, in einer Menge von Alternativen die beste bezüglich eines Zielkriteriums zu bestimmen.^[1] Ein Beispiel ist das Problem des Handlungsreisenden, also die Bestimmung einer kürzesten Rundreise durch eine Reihe von Städten. Die Modellierung und das Lösen von Optimierungsproblemen sind Teil der mathematischen Optimierung.

Mathematische Definition und Begriffe

Die Minimierung der Funktion $f(x)=(x-1)^{2}+2$ ergibt den Optimalpunkt $x^{\star }=1$ und den Optimalwert $v=2$ .^[2]

Ein Optimierungsproblem $P$ besteht aus einer reellwertigen Zielfunktion $f$ , einer zulässigen Menge $M$ , Entscheidungsvariablen $x$ und festen problemdefinierenden Eingangsdaten wie etwa den Abständen zwischen den zu besuchenden Städten des Problems des Handlungsreisenden oder dem Wert der Gegenstände im Rucksackproblem. Es ist gegeben durch

P:\qquad \min _{x}f(x)\quad {\text{s. t.}}\quad x\in M.

Üblicherweise ist hierbei $P$ in einen Raum $V$ , wie etwa den $\mathbb {R} ^{n}$ , eingebettet. In diesem Fall gelten $f:V\to \mathbb {R}$ , $M\subseteq V$ und $x\in V$ . Die Schreibweise ${\text{s. t.}}$ geht auf den englischen Ausdruck subject to zurück und bedeutet, dass bei der Suche nach der Lösung von $P$ nur sogenannte zulässige Punkte $x\in M$ infrage kommen. Da $\min$ die Optimierungsrichtung angibt, läge in diesem Fall ein Minimierungsproblem vor. Bei einem Maximierungsproblem sind Lösungen $x$ mit möglichst großen $f(x)$ gesucht, aber dieser Fall lässt sich durch Negieren von $f$ auf den vorherigen zurückführen. Falls $P$ lösbar ist, so gibt es mindestens einen Optimalpunkt $x^{\star }\in M$ mit $f(x^{\star })\leq f(x)$ für alle $x\in M$ und einen eindeutigen Optimalwert $v=f(x^{\star })$ . Zu beachten ist, dass der Optimalpunkt in der Regel ein hochdimensionaler Vektor ist (zum Beispiel die optimale Route im Falle des Problems des Handlungsreisenden) und der Optimalwert eine reelle Zahl ist (etwa die Länge der kürzesten Tour). Die zulässige Menge $M$ von $P$ wird in der Regel durch Gleichungen und Ungleichungen beschrieben und kann daher durch

M=\{x\in V|\ g_{i}(x)\leq 0,\ h_{j}(x)=0,\ i\in I,\ j\in J\}

dargestellt werden, wobei $I$ die Indexmenge der Ungleichungsrestriktionen und $J$ die Indexmenge der Gleichungsrestriktionen darstellt. Restriktionen werden auch als Nebenbedingungen oder Constraints bezeichnet.

Anmerkungen

Anstatt ein Optimierungsproblem algebraisch, also durch Gleichungen und Ungleichungen, zu beschreiben, ist es manchmal auch üblich, die Problemstellung in der Sprache der Graphentheorie zu formulieren. Dies passiert insbesondere oft in der kombinatorischen Optimierung wie beispielsweise bei der Formulierung des Problem des Handlungsreisenden.^[3]
Die funktionale Beschreibung eines Optimierungsproblems, das heißt die Wahl der Funktionen $f$ , $g_{i}$ und $h_{j}$ , ist in der Regel nicht eindeutig, sondern das Ergebnis eines Modellierungsprozesses, welcher eine ausreichend genaue Beschreibung der Anwendung bei einer möglichst guten Lösbarkeit des resultierenden Problems gewährleisten soll. Steht die Modellierung im Vordergrund, so spricht man auch von einem Optimierungsmodell.

Ausgewählte Beispiele

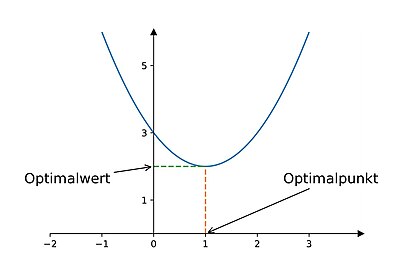
Das Optimierungsproblem $P:\qquad \min _{x\in \mathbb {R} ^{2}}x_{1}^{2}+x_{2}\quad {\text{s. t.}}\quad x_{2}\geq -1$ ist ein Optimierungsproblem mit eindeutigem Optimalpunkt $x^{\star }=(0,-1)$ und Optimalwert $v=-1$ .
Rucksackproblem
Problem des Handlungsreisenden
Transportproblem
Scheduling-Probleme (siehe ^[4] für eine Ausarbeitung als Optimierungsproblem)
Parameterschätzung in Statistik/Machine Learning durch Minimierung der Verlustfunktion (engl. loss function) etwa durch die Methode der kleinsten Quadrate oder die Methode der kleinsten absoluten Abweichungen
Probleme der Graphentheorie wie das Problem der kürzesten Pfade oder der Frage nach optimalen Flüssen und Schnitten in Netzwerken.

Klassifikation von Optimierungsproblemen

Optimierungsprobleme lassen sich anhand ihrer mathematischen Eigenschaften klassifizieren.

Falls $V$ unendlichdimensional ist, ist $P$ ein unendlichdimensionales Optimierungsproblem. Dies tritt etwa in der Variationsrechnung oder der optimalen Steuerung auf. Im Folgenden gehen wir von endlichdimensionalen Optimierungsproblemen aus.
Falls $P$ mehrere Zielfunktionen besitzt, sprechen wir von der Mehrzieloptimierung und bezeichnen $P$ als multikriterielles Optimierungsproblem. Im Folgenden gehen wir von Optimierungsproblemen mit einer Zielfunktion aus. Diese werden auch skalare Optimierungsprobleme genannt.
Falls $P$ keine Restriktionen besitzt, d. h. falls $M=V$ gilt, ist $P$ ein unrestringiertes Optimierungsproblem, andernfalls ist $P$ ein restringiertes Optimierungsproblem.
Falls $V=\mathbb {B} ^{n}$ gilt, d. h. alle Entscheidungsvariablen binär sind, $P$ keine Restriktionen besitzt und die Zielfunktion $f$ quadratisch ist, so spricht man von quadratischer unrestringierter binärer Optimierung (QUBO).
Falls $V=\mathbb {R} ^{n}$ gilt und die Zielfunktion $f$ sowie die Funktionen $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ linear sind, ist $P$ ein (kontinuierliches) lineares Optimierungsproblem (LP).
Falls $V=\mathbb {R} ^{n}$ gilt, die die Gleichungen definierende Funktionen $h_{j},\ j\in J,$ linear sind, und die Zielfunktion $f$ sowie ggf. Funktionen $g_{i},\ i\in I,$ quadratisch sind, ist $P$ ein (kontinuierliches) quadratisches Optimierungsproblem (QP) bzw. ein (kontinuierliches) quadratisches Optimierungsproblem mit quadratischen Nebenbedingungen (QCQP).
Falls $V=\mathbb {R} ^{n}$ gilt und $M$ eine konvexe Menge ist sowie die Zielfunktion $f$ konvexe Funktion, ist $P$ ein konvexes Optimierungsproblem. Man beachte, das die Zielfunktion nicht zwangsläufig differenzierbar sein muss, da auf das Subdifferential zurückgegriffen werden kann und auch die Funktionen $g_{i},\ i\in I,$ nicht selbst konvex sein müssen, um eine konvexe zulässige Menge zu definieren^[5]. Spezialfälle für konvexe Optimierungsprobleme sind konische Optimierungsprobleme (insbesondere semi-definite und Second-Order-Cone Probleme) und geometrische Optimierungsprobleme.
Falls $V=\mathbb {R} ^{n}$ gilt und beliebig viele der Funktionen $f$ , $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ beliebig nichtlinear (jedoch meistens stetig differenzierbar) sind, ist $P$ ein nichtlineares Optimierungsproblem (NLP).
Falls $V=\mathbb {Z} ^{n}$ gilt und die Zielfunktion $f$ sowie die Funktionen $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ linear sind, ist $P$ ein ganzzahliges lineares Optimierungsproblem (ILP).
Falls $V=\mathbb {R^{n}} \times \mathbb {Z^{m}}$ gilt, d. h. falls einige der Entscheidungsvariablen kontinuierlich und andere ganzzahlig sind, und die Zielfunktion $f$ sowie die Funktionen $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ linear sind, ist $P$ ein gemischt-ganzzahliges lineares Optimierungsproblem (MILP oder MIP).
Falls $V=\mathbb {R^{n}} \times \mathbb {Z^{m}}$ gilt und beliebig viele der Funktionen $f$ , $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ quadratisch sind, ist $P$ ein gemischt-ganzzahliges quadratisches Optimierungsproblem (MIQP oder ggf. MIQCP)
Falls $V=\mathbb {R^{n}} \times \mathbb {Z^{m}}$ gilt und beliebig viele der Funktionen $f$ , $g_{i},\ i\in I,$ und $h_{j},\ j\in J,$ beliebig nichtlinear sind, ist $P$ ein gemischt-ganzzahliges nichtlineares Optimierungsproblem (MINLP)
Falls $V=\mathbb {Z} ^{n}$ gilt, ist $P$ ein kombinatorisches Optimierungsproblem.
Falls $V=\mathbb {R} ^{n}$ gilt und $P$ (abzählbar) unendlich viele Gleichungsrestriktionen besitzt, ist $P$ ein semi-infinites Optimierungsproblem (SIP).

Optimierungsmethoden

→ Hauptartikel: Mathematische Optimierung#Optimierungsmethoden

Einen Algorithmus, der ein Optimierungsproblem löst, nennt man Optimierungsmethode oder Optimierungsalgorithmus. Je nach Klasse des Optimierungsproblems kommen verschiedene Verfahren zum Einsatz. Neben spezialisierten Verfahren, wie etwa dem Dijkstra-Algorithmus zur Bestimmung kürzester Wege gibt es auch allgemeine Lösungsverfahren, welche anwendungsunabhängig basierend auf der Kenntnis der Problemklasse eingesetzt werden können. Am bekanntesten sind vermutlich die Verfahren der nichtlinearen Optimierung zur Bestimmung lokaler Optimalpunkte wie das Gradientenverfahren, das Newtonverfahren und Quasi-Newton-Verfahren. Für die Minimierung der Verlustfunktion im Bereich Machine Learning werden typischerweise leichtfüßige Varianten des Gradientenverfahrens wie das stochastische Gradientenverfahren (stochastic gradient descent) eingesetzt. Für LPs kommen das Simplex-Verfahren sowie Innere-Punkte-Methoden zum Einsatz, wobei letztgenannte auch zur Lösung nichtlinearer konvexer Optimierungsprobleme verwendet werden. Optimierungsprobleme, in denen auch ganzzahlige Variablen auftreten, können exakt mit Branch-and-Bound sowie Branch-and-Cut Methoden gelöst werden. Darüber hinaus können auch anwendungsspezifische Heuristiken wie die Nearest-Neighbor-Heuristik oder allgemeine Metaheuristiken eingesetzt werden, die in der Regel jedoch keine Aussage über die Qualität der gefundenen Lösung treffen.

Einzelnachweise

↑ Oliver Stein: Grundzüge der Globalen Optimierung. 2. Auflage. Springer Spektrum, Berlin / Heidelberg 2021, ISBN 978-3-662-62533-0, doi: 10.1007/978-3-662-55360-2.
↑ Nathan Sudermann-Merx: Einführung in Optimierungsmodelle. Springer, Berlin / Heidelberg 2023, ISBN 978-3-662-67380-5, doi: 10.1007/978-3-662-67381-2.
↑ Bernhard Korte, Jens Vygen: Combinatorial optimization: theory and algorithms (= Algorithms and combinatorics). 5. Auflage. Springer, Berlin Heidelberg 2012, ISBN 978-3-642-24487-2 ( uni-muenchen.de [PDF]).
↑ Christodoulos A. Floudas, Xiaoxia Lin: Mixed Integer Linear Programming in Process Scheduling: Modeling, Algorithms, and Applications. In: Annals of Operations Research. Band 139, Nr. 1, Oktober 2005, ISSN 0254-5330, S. 131–162, doi: 10.1007/s10479-005-3446-x ( umich.edu [PDF]).
↑ Stephen P. Boyd, Lieven Vandenberghe: Convex optimization. 29. Auflage. Cambridge University Press, Cambridge / New York / Melbourne / New Delhi / Singapore 2023, ISBN 978-0-521-83378-3 ( stanford.edu [PDF; 6,9 MB;]).

Basierend auf einem Artikel in:

Wikipedia.de