Nichtlineare Optimierung
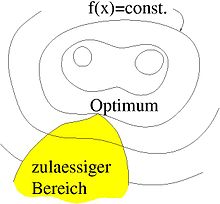
In der Mathematik ist die nichtlineare Optimierung (auch nichtlineares Programm, NLP, genannt) das Vorhaben, eine skalare Zielfunktion einer oder mehrerer reeller Variablen in einem eingeschränkten Bereich zu optimieren, wobei die Zielfunktion oder die Bereichsgrenzen nicht linear (affin) sind. Es ist ein Teilgebiet der mathematischen Optimierung und ein Obergebiet der konvexen Optimierung. In Abgrenzung von den genannten Begriffen wird hier die Anwendung auf differenzierbare nichtlineare Zielfunktionen ohne Beschränkung auf Konvexität der Zielfunktion oder des Suchbereiches beschrieben. Unter Begriffe: Zielfunktion, Nebenbedingungen, zulässige Menge, lokale und globale Optimierung finden sich wesentliche Erklärungen.
Anwendungsfelder
Nichtlineare Programme finden sich in vielfältiger Weise in der Wissenschaft und im Ingenieurwesen.
In der Wirtschaftswissenschaft kann es darum gehen, die Kosten eines Prozesses zu minimieren, der Einschränkungen in der Verfügbarkeit der Mittel und Kapazitäten unterliegt. Die Kostenfunktion kann darin nichtlinear sein. In der theoretischen Mechanik findet sich im Hamiltonschen Prinzip ein Extremalprinzip, dessen Lösung bei nichtlinearen Randbedingungen ein nichtlineares Programm darstellt.
Moderne Ingenieuranwendungen beinhalten oft und in komplizierter Weise Optimierungsaufgaben. So kann es darum gehen, das Gewicht eines Bauteils zu minimieren, das gleichzeitig bestimmten Anforderungen (z.B. Einschränkungen des Bauraumes, Obergrenzen für Verformungen bei gegebenen Lasten) genügen muss.
Bei der Anwendung eines mathematischen Modells kann es darum gehen, die Parameter des Modells an gemessene Werte anzupassen. Nichtlineare Einflüsse der Parameter und Einschränkungen an die Parameter (z.B. dass nur positive Werte zugelassen sind) führen hier auf ein nichtlineares Programm.
In diesen Fragestellungen ist oftmals nicht a priori bekannt, ob das gestellte Problem konvex ist oder nicht. Manchmal beobachtet man eine Abhängigkeit der gefundenen optimalen Lösung vom Startpunkt der Suche. Dann hat man lokale Optima gefunden und das Problem ist mit Sicherheit nicht konvex.
Problemdefinition
Es gibt viele mögliche Formulierungen eines nicht linearen Programms. An
dieser Stelle soll eine möglichst allgemeine Form gewählt werden. Der
Eingabeparameter
sei aus dem
,
das heißt, das Problem hängt von
Einflussparametern ab, die im Vektor
eingelagert sind. Die Zielfunktion
sei einmal stetig differenzierbar. Weiterhin seien die Nebenbedingungen (NB) in
Ungleichheitsform
mit
und in Gleichheitsform
mit
gegeben und einmal stetig differenzierbar. Dann lautet das Problem
mathematisch:
.
Der zulässige Bereich
wird von den Nebenbedingungen (NB) eingeschränkt: Für alle Werte der Parameter
aus dem zulässigen Bereich (
)
sollen die NB erfüllt sein. Zulässig ist das Problem
,
wenn der zulässige Bereich
nicht leer ist.
Zumeist beschränkt sich die theoretische Behandlung der nicht linearen
Optimierung auf Minimierungsprobleme. In der Tat kann das Maximierungsproblem
einer Funktion
in ein Minimierungsproblem von
oder
,
falls
gesichert ist, umformuliert werden.
Vorgehen
Das Problem wird mit den unten beschriebenen Verfahren auf die Optimierung einer Hilfsfunktion ohne NB zurückgeführt. Um sich die gradientenbasierten Methoden zu Nutze machen zu können, teilt man das abzusuchende Gebiet gegebenenfalls in solche auf, in denen die Zielfunktion differenzierbar ist. Wenn möglich, sollten die Teilgebiete konvex sein und die Zielfunktion in ihnen auch. Dann kann man die globalen Extrema in den Teilgebieten mit den in Mathematische Optimierung und Konvexe Optimierung aufgeführten Verfahren berechnen und das optimale auswählen.
Die Konstruktion der Hilfsfunktion soll anhand eines Beispiels erläutert
werden: Zwei Kugeln in einer Mulde versuchen den tiefstmöglichen Punkt
einzunehmen, dürfen sich dabei aber nicht durchdringen. Die Zielfunktion ist
also die Lageenergie
der Kugeln und nimmt im Gleichgewicht ein Minimum an. Die Nebenbedingung
würde hier die Durchdringung der Kugeln
und
bezeichnen, wobei mit negativer Durchdringung ein positiver Abstand gemeint
wird.
- Lagrange-Multiplikatoren: Die NB werden mit reellen Faktoren, den Lagrange-Multiplikatoren, multipliziert und in die Zielfunktion eingebaut, so dass bei positiven Lagrange-Multiplikatoren die Verletzung der NB bestraft wird. Die so erhaltene Hilfsfunktion heißt Lagrange-Funktion. Die Lagrange-Multiplikatoren werden als Unbekannte in das Problem eingeführt und müssen ebenfalls bestimmt werden. Bei den Kugeln sind die Lagrange-Multiplikatoren gerade die Kontaktkräfte, die die Kugeln bei Berührung aufeinander ausüben, so dass sie sich nicht durchdringen.
- Barrierefunktionen: Die NB werden mit Barrierefunktionen dargestellt, die
bei Annäherung an die Grenze des Definitionsbereiches positive Werte annehmen
und auf der Grenze ins Unendliche wachsen. Die Barrierefunktionen werden mit
Barriereparametern
multipliziert und in die Zielfunktion eingebaut, so dass die Annäherung an die Grenze bestraft wird und so die Verletzung der NB verhindert wird. Im Kugelbild bekämen die Kugeln einen mehr oder weniger dicken Mantel, der immer steifer wird, je stärker er bei Berührung zusammengedrückt wird. Eine Verletzung der NB wird so verhindert zu dem Preis, dass bereits die Annäherung an die Bereichsgrenze bestraft wird. Die Methode wird bei Innere-Punkte-Verfahren angewendet.
- Straffunktionen: Die Straffunktionen werden wie die Barrierefunktionen
eingesetzt. Die NB werden mit Straffunktionen dargestellt, die im zulässigen
Bereich verschwinden und bei Verletzung der NB positiv sind. Die
Straffunktionen werden mit Strafparametern
multipliziert und in die Zielfunktion eingebaut, so dass die Verletzung der NB bestraft wird, daher der Name. Hier werden aktive NB evtl. verletzt und die Zulässigkeit der Lösung muss geprüft werden. Im Kugel-Bild entspricht die Straffunktion der „echten“ Durchdringung (die bei positivem Abstand der Kugeln verschwindet) und der Strafparameter einer Federsteifigkeit. Die Feder versucht eindringende Punkte wieder an die Oberfläche zu ziehen. Je steifer die Feder ausfällt, desto geringer wird die Eindringung sein.
- Erweiterte Lagrange-Methode (englisch augmented Lagrange method): Dies ist eine Kombination der Lagrange-Multiplikatoren und der Strafmethode. Der Lagrange-Multiplikator wird iterativ anhand der Verletzung der NB bestimmt.
- Trivial (und deshalb in den Quellen oftmals nicht behandelt), aber doch zu erwähnen und im praktischen Gebrauch ist, dass aktive NB dazu genutzt werden können, Variable zu eliminieren. Die Variablen werden auf Werte festgelegt, derart dass eine Verletzung der NB nunmehr unmöglich ist. Im Kugel-Bild würde man Berührungspunkte der Kugeln aneinanderkoppeln (ihre Koordinaten gleichsetzen), so dass eine Durchdringung (dort) nicht mehr stattfinden kann.
Die Vor- und Nachteile der beschriebenen Methoden sind in der Tabelle zusammengefasst:
| Methode | Vorteile | Nachteile |
|---|---|---|
| Lagrange-Multiplikatoren |
|
|
| Barrierefunktionen |
|
|
| Strafverfahren | Für |
|
| Erweiterte Lagrange-Methode |
|
Benötigt mehrere konvergierte Lösungen des globalen Problems. |
| Eliminierung der Freiheitsgrade |
|
Ist nur anwendbar, wenn die Aktivität der NB bekannt ist. |
Theorie der Optimierung
Isolierte Punkte
In einem nicht linearen Programm können NB den zulässigen Bereich in einigen
Punkten
derart einschränken, dass zwar
aber kein Punkt in seiner Umgebung
im zulässigen Bereich liegt. Mathematisch formuliert heißt das, dass es eine
Umgebung
gibt, so dass
gilt. Isolierte Punkte müssen alle einzeln, jeder für sich, auf Optimalität geprüft werden.
Regularitäts-Bedingungen, Tangenten- und Linearisierender Kegel
Für die Formulierung von Optimalitätsbedingungen müssen die NB gewisse Anforderungen erfüllen, engl. constraint qualifications (CQ). Unter Anderem geht es darum, optimale Punkte aus der Betrachtung auszuschließen, die isoliert sind oder in denen es redundante NB gibt. Es existieren mehrere unterschiedlich scharfe Formulierungen, welche die Erfüllung dieser CQ sicherstellen. Punkte, in denen die Anforderungen erfüllt sind, heißen regulär. Irreguläre Punkte, in denen keine dieser Anforderungen greift, müssen ausgeschlossen oder gesondert betrachtet werden.
Zentral für die Formulierung der Anforderungen an die NB und der
Optimalitätsbedingungen ist der Begriff Tangentenkegel
und Linearisierender
Kegel. Um sich diese anschaulich klarzumachen, stellt man sich an einen
Punkt
im zulässigen Gebiet und läuft unter Beachtung der NB (die NB kann man sich als
undurchdringliche Wände vorstellen) zum Zielpunkt
.
Der Tangentenkegel ist dann die Menge aller möglichen Richtungen aus denen man
im Zielpunkt
ankommen kann. Beim linearisierenden Kegel werden zunächst die NB linearisiert,
d.h. durch ihre Tangenten im Zielpunkt
ersetzt. Der linearisierende Kegel ist dann die Menge aller möglichen
Richtungen, aus denen man unter Beachtung der linearisierten NB im Zielpunkt
ankommen kann. Der Tangentenkegel und Linearisierende Kegel unterscheiden sich
dort, wo zwei Wände am Standort parallel verlaufen und der Zielpunkt
sozusagen in einem Gang (der Breite 0) liegt. Im linearisierenden Kegel kann man
dann aus beiden Richtungen des Gangs ankommen, er linearisierte ja die
Wände. Wenn die zunächst parallelen Wände in einer Richtung unmittelbar ihre
Parallelität verlieren und den Gang zumachen, so dass kein noch so kleiner
Schritt in diese Richtung möglich ist, kann man im Tangentenkegel nur aus der
offenen Richtung in
ankommen. Das ist der Unterschied, siehe den ersten pathologischen Fall unten.
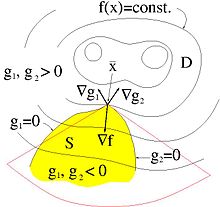
In der Grafik stimmen Tangentenkegel und Linearisierender Kegel im optimalen
Punkt überein und sind rot angedeutet.
Die Anforderungen an die NB stellen sicher, dass im optimalen Punkt der Tangentenkegel und der linearisierende Kegel übereinstimmen und der optimale Punkt nicht isoliert ist. Die Übereinstimmung von linearisierenden Kegel und Tangentialkegel wird manchmal auch als eigene Regularitätsbedingung aufgeführt und Abadie Constraint Qualification genannt. Beispiele für Regularitätsbedingungen sind:
- Slater-Bedingung
(nur für konvexe Probleme): Es gibt einen Punkt
, so dass
für alle
und alle Gleichungsnebenbedingungen in
erfüllt sind. An dieser Stelle sei erwähnt, dass die Constraint Qualification von Slater im Allgemeinen als die Wichtigste angesehen wird.
- Lineare
Unabhängigkeit – linear independence constraint
qualification (LICQ): Die Gradienten der aktiven
Ungleichungsbedingungen und die Gradienten der Gleichungsbedingungen sind
linear unabhängig im Punkt
.
- Mangasarian-Fromovitz
– Mangasarian-Fromovitz constraint qualification
(MFCQ): Die Gradienten der aktiven Ungleichungsbedingungen und die
Gradienten der Gleichungsbedingungen sind positiv-linear unabhängig im Punkt
.
- Konstanter Rang – constant rank constraint
qualification (CRCQ): Für jede Untermenge der Gradienten der
Ungleichungsbedingungen, welche aktiv sind, und der Gradienten der
Gleichungsbedingungen ist der Rang in der Nähe von
konstant.
- Konstante positive-lineare Abhängigkeit – constant
positive-linear dependence constraint qualification (CPLD): Für
jede Untermenge der Gradienten, der Ungleichungsbedingungen, welche aktiv
sind, und der Gradienten der Gleichungsbedingungen, und falls eine
positive-lineare Abhängigkeit im Punkt
vorliegt, dann gibt es eine positiv-lineare Abhängigkeit in der Nähe von
.
Man kann zeigen, dass die folgenden beiden Folgerungsstränge gelten
und
,
obwohl MFCQ nicht äquivalent zu CRCQ ist. In der Praxis werden schwächere Constraint Qualifications bevorzugt, da diese stärkere Optimalitäts-Bedingungen liefern.
Pathologische Fälle
Die CQ sind dazu da, Zustände wie im Ursprung in folgenden Beispielen von der Betrachtung auszuschließen:
- Minimiere
unter den NB
und
.
- Minimiere
unter der NB
.
- Minimiere
unter der NB
.
Optimalitätsbedingungen
Notwendige Bedingung
Karush-Kuhn-Tucker-Bedingungen
Die Karush-Kuhn-Tucker-Bedingungen sind ein notwendiges
Optimalitätskriterium erster Ordnung und eine Verallgemeinerung der
notwendigen Bedingung
von Optimierungsproblemen ohne Nebenbedingungen sowie der Lagrange-Multiplikatoren
für Optimierungsprobleme unter Gleichungsnebenbedingungen. In Worten bedeutet
der Satz von Karush-Kuhn-Tucker ungefähr, dass wenn
ein zulässiger, regulärer und optimaler Punkt ist, sich der Gradient der
Zielfunktion
als positive Linearkombination der Gradienten der aktiven NB darstellen lässt,
siehe auch das Bild oben.
Sei
die Zielfunktion und die Funktionen
mit
und die Funktionen
mit
sind Nebenbedingungs-Funktionen. Alle vorkommenden Funktionen
seien einmal stetig
differenzierbar. Es sei
ein regulärer Punkt, das heißt, eine der Regularitätsanforderung (CQ) von oben
ist erfüllt. Falls
ein lokales Optimum ist, dann existieren Konstanten
und
so dass
("+" bei Minimierung, "-" bei Maximierung),
für alle
,
für alle
.
Jeder Punkt, in dem diese Bedingungen erfüllt sind, heißt Karush-Kuhn-Tucker-Punkt (kurz: KKT-Punkt).
Ist
ein Punkt des zulässigen Gebietes in dem keine NB aktiv sind, insbesondere keine
Gleichheitsnebenbedingungen
vorliegen, dann sind wegen
alle
und die obigen Bedingungen reduzieren sich auf die bekannte notwendige Bedingung
unrestringierter Probleme
.
Fritz-John-Bedingungen
Die Fritz-John-Bedingungen (oder kurz FJ-Bedingungen) sind genau wie die KKT-Bedingungen ein Optimalitätskriterium erster Ordnung. Im Gegensatz zu den KKT-Bedingungen kommen sie ohne Regularitätsbedingungen aus, liefern aber eine schwächere Aussage. Unter Umständen stimmen sie mit den KKT-Bedingungen überein.
Ist
ein zulässiger Punkt, der lokal Optimal ist, dann existieren
so dass
("+" bei Minimierung, "-" bei Maximierung),
für alle
,
für alle
.
und
ungleich dem Nullvektor ist.
Jeder Punkt, in dem diese Bedingungen erfüllt sind, heißt
Fritz-John-Punkt oder kurz FJ-Punkt. Die FJ-Bedingungen unterscheiden
sich nur durch Einführung des Skalars
vor dem Gradient der Zielfunktion.
Hinreichende Bedingungen
Ist
ein KKT-Punkt und die Richtung des steilsten Auf- bzw. Abstiegs schließt mit den
Flanken des Tangentenkegels einen Winkel kleiner als 90° ein, dann ist
ein minimaler bzw. maximaler Punkt. Mathematisch: Gilt
für alle
,
dann ist
ein lokales Minimum (bzw. Maximum). Dies ist ein hinreichendes
Optimalitätskriterium erster Ordnung. Ein hinreichendes
Optimalitätskriterium zweiter Ordnung für einen KKT-Punkt
besagt, dass wenn
ein stationärer Punkt und die Hesse-Matrix der Zielfunktion ist positiv
(negativ) definit für alle Vektoren aus dem Tangentenkegel, dann ist
ein lokales Minimum (bzw. Maximum). Mathematisch:
und
für alle
.
Darin ist
der Tangentenkegel, siehe Regularitäts-Bedingungen,
Tangenten- und Linearisierender Kegel.
Sätze zu den Näherungsverfahren
- Im Grenzwert der gegen null gehenden Barriereparameter geht die mit Barrierefunktionen gefundene Lösung in die mit den Lagrange Multiplikatoren gefundene Lösung über.
- Im Grenzwert der gegen unendlich gehenden Strafparameter geht die mit Straffunktionen gefundene Lösung in die mit den Lagrange Multiplikatoren gefundene Lösung über.
- Im Grenzwert unendlich vieler Iterationen strebt die mit der erweiterten Lagrange Methode gefundene Lösung auch gegen die mit den Lagrange Multiplikatoren gefundene Lösung.
Beispiel
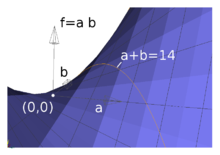
Anhand eines einfachen Beispiels sollen die oben genannten fünf Methoden der Lösung eines Problems erläutert werden. In dem Problem soll das Produkt zweier positiver reeller Zahlen maximiert werden, deren Summe höchsten sechzehn beträgt. Mathematisch formuliert heißt das: Gesucht wird
mit der NB
.
Es ist anschaulich klar, dass im Optimum die NB aktiv ist, sonst könnte
leicht eine bessere Lösung gefunden werden. Der einzige stationäre Punkt mit
dieser in
und
linearen Funktion liegt in
weswegen die Suche manchmal in diese Richtung geht. Dann muss man die NB
gewissermaßen „in den Weg legen“, damit der Algorithmus sie „bemerkt“.
Eliminierung der Freiheitsgrade
Aus der als aktiv erkannten NB ermittelt man
und die Hilfsfunktion hängt nur noch von
ab, so dass die Lösung mittels Kurvendiskussion berechnet werden kann:
Man sieht:
- Die Hilfsfunktion hat nur noch eine Variable.
- Die Lösung ist korrekt, denn es handelt sich um ein Maximum.
- Das Verfahren findet vor allem dann Anwendung, wenn bekannt ist, dass die NB aktiv ist, z.B. im Kontakt fest verklebter Bauteile.
Lagrange-Multiplikator
Hier wird die -fache
NB von der Zielfunktion subtrahiert, worin der Faktor
der Lagrange-Multiplikator ist und wie eine zusätzliche Unbekannte behandelt
wird. Die Subtraktion wird gewählt, damit eine Verletzung der NB bei
bestraft wird. Die Hilfs- oder Lagrange-Funktion lautet hier also:
.
Im Minimum verschwinden alle Ableitungen nach allen Variablen:
und die Lösung
ist gefunden. Wegen
und
ist die Karush-Kuhn-Tucker-Bedingung erfüllt. Das obige Gleichungssystem kann
als Matrizengleichung geschrieben werden:
Die Methode der lagrangeschen Multiplikatoren
- erfüllt die NB exakt,
- führt zusätzliche Unbekannte (
) ein,
- schleust verschwindende Diagonalelemente in das Gleichungssystem ein, die bei Anwendung der Cholesky-Zerlegung problematisch sind.
- kann anhand des Vorzeichens von
beurteilen, ob die Nebenbedingung aktiv ist oder nicht (positiv bei Aktivität).
Barrierefunktion
Mit Barrierefunktionen können Neben-Bedingungen mit Sicherheit erfüllt werden
zu dem Preis, dass im Optimum die NB nicht ausgereizt wird. Bei der Suche nach
einer Lösung wird zur Ziel-Funktion
das
-fache
einer Barrierefunktion hinzu addiert, z.B.:
.
Darin ist
eine logarithmische Barrierefunktion und
der Barriereparameter. Im Extremum verschwinden wieder alle Ableitungen:
,
und daher
sowie
, was die Lösung
besitzt, die für
die Lösungen
annimmt. Bei der iterativen Suche mit dem Newton-Raphson Verfahren bekommt man
die Vorschrift
für die Berechnung des Inkrements
und
.
Die Determinante der Hesse-Matrix
lautet:
.
Man sieht:
- Die Nebenbedingung wird eingehalten.
- Im Grenzwert
erhält man die exakte Lösung.
- Für
existiert kein optimaler Punkt. Allgemein stimmen die Höhenlinien der Hilfsfunktion nicht mit denen der Zielfunktion überein.
- Bei Annäherung an die Lösung und mit
kann die Hesse-Matrix schlecht konditioniert sein.
- Bei einer inkrementellen Suche muss sichergestellt werden, dass das Inkrement in den Unbekannten nicht so groß ist, dass man aus Versehen auf der falschen Seite der Barriere landet, wo die Barrierefunktion in diesem Beispiel nicht definiert ist.
Strafverfahren
Mit Straf-Verfahren können Neben-Bedingungen näherungsweise erfüllt werden.
Bei der Suche nach einer Lösung wird von der Ziel-Funktion
das
-fache
einer Straffunktion abgezogen (soll ja die Verletzung bestrafen):
.
Darin ist
der Straf-Parameter und
die Straffunktion. Mit
nennt man die Straffunktion exakt, sie ist aber nicht differenzierbar.
Hier soll
benutzt werden. Im Extremum verschwinden wieder alle Ableitungen:
.
Mit
bekommt man
weswegen man hier im „verbotenen“ Gebiet
starten muss. Dann folgt aus
das Gleichungssystem
mit der Lösung
,
die für
in die Lösung
übergeht.
Man sieht:
- Die Nebenbedingung wird nur näherungsweise erfüllt aber mit wachsendem Strafparameter immer besser, allerdings nur weil hier exakt gerechnet werden kann. Bei numerischer Lösung des Gleichungssystems würden Rundungsfehler mit wachsendem Strafparameter zu Fehlern führen.
- Der Grund hierfür liegt darin, dass mit zunehmendem Strafparameter der
Wert der Determinante des Gleichungssystems
gegen null geht. Das Problem ist zunehmend schlecht gestellt.
- Es muss ein Kompromiss hinsichtlich der Konditionierung des Gleichungssystems und der Genauigkeit der Erfüllung der NB gefunden werden.
- Durch Einsetzen von
und
in die NB kann geprüft werden, wie stark sie verletzt wird.
- Es werden keine zusätzlichen Variablen oder verschwindende
Diagonalelemente eingeschleust, es existiert eine Lösung für alle
Strafparameter
und das Verfahren gilt als numerisch robust.
Erweiterte oder verallgemeinerte-Lagrange-Methode
Die erweiterte oder verallgemeinerte Lagrange-Methode (englisch augmented-lagrange-method)
benutzt die Straffunktion, um die Lagrange-Multiplikatoren näherungsweise zu
berechnen. Bei der Suche nach einer Lösung wird von der Zielfunktion
das
-fache
der NB und das
-fache
einer Straffunktion abgezogen (Strafidee):
.
Im Extremum verschwinden alle Ableitungen:
.
Mit
bekommt man
.
Andernfalls entsteht aus
das Gleichungssystem
,
das die Lösung
hat.
Die numerische Suche des Extremums mit der erweiterten Lagrange-Methode
- startet normalerweise mit
und den Anfangswerten
,
- berechnet
und
(im nicht-linearen Fall Iteration bis zur Konvergenz),
- setzt
und
- bricht ab, wenn ein geeignetes Konvergenzkriterium erfüllt ist oder
inkrementiert
und kehrt in Schritt 2 zurück.
Hier muss allerdings ein Startwert mit
vorgegeben werden, damit der Punkt
gefunden werden kann. Mit
und
ergibt sich bis zu einem Fehler
folgender Iterationsverlauf:
| 1 | 8.04020100503 | −91.959798995 | 8.04020100502 | 64.6448322012 | 0.0804020100502 |
| 2 | 7.9997979849 | −0.0404030201258 | 7.9997979849 | −0.648064402007 | −0.000404030201256 |
| 3 | 8.00000101515 | 0.000203030251889 | 8.00000101515 | 0.00324844322116 | 2.03030252166e-06 |
| 4 | 7.9999999949 | −1.02025252513e-06 | 7.9999999949 | −1.63240414395e-05 | −1.02025285997e-08 |
| 5 | 8.00000000003 | 5.12689890542e-09 | 8.00000000003 | 8.20303824867e-08 | 5.12692110988e-11 |
| 6 | 8.0 | −2.57633914202e-11 | 8.0 | −4.12214262724e-10 | −2.57571741713e-13 |
Mit einem größeren Straf-Parameter wäre die Konvergenz schneller, das Beispiel aber weniger illustrativ.
Die erweiterte Lagrange-Methode
- erfüllt die NB beliebig genau,
- führt weder neue Unbekannte ein noch beeinträchtigt sie die Konditionierung des Gleichungssystems,
- benötigt dazu mehrere konvergierte Lösungen des globalen Problems (im zweiten Schritt) und
- kann die Aktivität der Neben-Bedingung an
messen.
Literatur
- R. Reinhardt, A. Hoffmann, T. Gerlach: Nichtlineare Optimierung. Springer, 2013, ISBN 978-3-8274-2948-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.04. 2020