`p`-Wert

Der p-Wert (nach Ronald Aylmer Fisher), auch Überschreitungswahrscheinlichkeit, oder Signifikanzwert genannt (p für lateinisch probabilitas = Wahrscheinlichkeit), ist in der Statistik und dort insbesondere in der Testtheorie ein Evidenzmaß für die Glaubwürdigkeit der Nullhypothese, d. h. er gibt an inwieweit die Beobachtungen die Nullhypothese (meist besagt sie, dass ein bestimmter Zusammenhang nicht besteht, z. B. ein neues Medikament ist nicht wirksam) „stützen“. Er ist definiert als die Wahrscheinlichkeit – unter der Bedingung, dass die Nullhypothese in Wirklichkeit gilt – den beobachteten Wert der Prüfgröße oder einen in Richtung der Alternative „extremeren“ Wert zu erhalten. Der p-Wert kann als das kleinste Signifikanzniveau interpretiert werden, bei dem die Nullhypothese gerade noch verworfen werden kann. Da der p-Wert eine Wahrscheinlichkeit ist, kann er Werte von null bis eins annehmen. Dies bietet den Vorteil, dass er die Vergleichbarkeit verschiedener Testergebnisse ermöglicht. Der konkrete Wert wird durch die gezogene Stichprobe bestimmt. Ist der p-Wert „klein“ (kleiner als ein vorgegebenes Signifikanzniveau; allgemein < 0,05), so lässt sich die Nullhypothese ablehnen. Anders ausgedrückt: Ist die errechnete Prüfgröße größer als der kritische Wert (kann unmittelbar aus einer Quantiltabelle abgelesen werden), so kann die Nullhypothese verworfen werden und man kann davon ausgehen, dass die Alternativhypothese gilt und damit ein bestimmter Zusammenhang besteht (z. B. ein neues Medikament ist wirksam). Wenn die Nullhypothese zugunsten der Alternativhypothese verworfen wird, wird das Resultat als „statistisch signifikant“ bezeichnet. „Signifikant“ bedeutet hierbei lediglich „überzufällig“ und ist nicht gleichbedeutend mit „praktischer Relevanz“ oder „wissenschaftlicher Bedeutsamkeit“. In verschiedenen wissenschaftlichen Disziplinen haben sich festgesetzte Grenzen wie 5 %, 1 % oder 0,1 % etabliert, die verwendet werden, um zu entscheiden, ob die Nullhypothese abgelehnt werden kann oder nicht. Die Größe des p-Werts gibt keine Aussage über die Größe des wahren Effekts.

Der p-Wert wird sehr häufig fehlinterpretiert und falsch verwendet, weswegen sich die American Statistical Association im Jahr 2016 genötigt sah, eine Mitteilung über den Umgang mit p-Werten und statistischer Signifikanz zu veröffentlichen. Einer kleinen kanadischen Feldstudie von 2019 zufolge werden in etlichen Lehrbüchern die Begriffe „p-Wert“ und „statistische Signifikanz“ nicht korrekt vermittelt. Studien von Oakes (1986) und Haller & Krauss (2002) zeigen, dass ein Großteil von Studierenden und von Lehrern der Statistik den p-Wert nicht korrekt interpretieren können. Die falsche Verwendung und die Manipulation von p-Werte ist eine Kontroverse in der Meta-Forschung.

Mathematische Formulierung

Bei einem statistischen Test wird eine Vermutung (Nullhypothese) $H_{0}$ überprüft, indem ein passendes Zufallsexperiment durchgeführt wird, das die Zufallsgrößen $X_1, X_2, \dotsc, X_n$ liefert. Diese Zufallsgrößen werden zu einer einzelnen Zahl, Prüfgröße genannt, zusammengefasst:

$T=u(X_{1},X_{2},\dotsc ,X_{n})$

Für einen konkreten Versuchsausgang $X_{1}=x_{1},X_{2}=x_{2},\dotsc ,X_{n}=x_{n}$ des Experiments erhält man einen Wert

$t=u(x_{1},x_{2},\dotsc ,x_{n})$ .

Der -Wert ist definiert als die Wahrscheinlichkeit – unter der Bedingung, dass die Nullhypothese $H_{0}$ in Wirklichkeit gilt – den beobachteten Wert der Prüfgröße oder einen in Richtung der Alternative „extremeren“ Wert zu erhalten. Für zusammengesetzte Nullhypothesen ist diese bedingte Wahrscheinlichkeit nur noch nach oben abschätzbar.

Bei einem rechtsseitigem Test gilt:

$p_{\text{rechts}}:=P(T\geq t\mid H_{0}).$

Bei einem linksseitigem Test gilt:

$p_{\text{links}}:=P(T\leq t\mid H_{0}).$

Und bei einem zweiseitigem Test gilt:

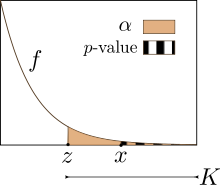
$p=2\cdot \min\{p_{\text{rechts}},p_{\text{links}}\}.$

Für diese Realisierung im Ablehnbereich ist der -Wert kleiner als $\alpha$ , oder dazu äquivalent ist die Realisierung der Prüfgröße x größer als der kritische Wert z. Hier ist die Wahrscheinlichkeitsdichte der Verteilung unter der Nullhypothese

Üblicherweise wird vor dem Test ein Signifikanzniveau $\alpha$ festgelegt und der -Wert dann mit diesem verglichen. Je kleiner der -Wert ist, desto mehr Grund gibt es, die Nullhypothese zu verwerfen. Ist der -Wert kleiner als das vorgegebene Signifikanzniveau $\alpha$ , so wird die Nullhypothese verworfen. Ansonsten kann man die Nullhypothese nicht verwerfen.

Nach frequentistischer Sichtweise enthält der von R. A. Fisher eingeführte -Wert keine weiterführende Information; nur die Tatsache, ob er kleiner ist als ein vorgegebenes Niveau $\alpha$ , ist von Interesse. In dieser Form ist $p\leq \alpha$ nur eine andere Formulierung dafür, dass der beobachtete Wert der Prüfgröße in der kritischen Region liegt, und fügt der Neyman-Pearsonschen Theorie der Hypothesentests nichts Neues hinzu.

Beispiel

Gegeben sei eine Münze. Die zu prüfende Nullhypothese $H_{0}$ sei, dass die Münze fair ist, dass also Kopf und Zahl gleich wahrscheinlich sind; die Alternativhypothese sei, dass ein Ergebnis wahrscheinlicher ist, wobei nicht festgelegt wird, welches der beiden wahrscheinlicher sein soll. Das Zufallsexperiment zum Testen der Nullhypothese bestehe nun darin, dass die Münze zwanzig Mal geworfen wird. bezeichne die Anzahl der Würfe, die „Kopf“ als Ergebnis liefern. Bei einer fairen Münze wäre zehnmal „Kopf“ zu erwarten. Als Statistik wählt man daher sinnvollerweise

$Y=|K-10|$ .

Angenommen, der Versuch liefert k=14 -mal das Ergebnis „Kopf“, also ist die Realisierung von hier y=4 . Unter der Nullhypothese ist die Anzahl der Köpfe binomialverteilt mit n=20 und $p=\tfrac{1}{2}$ . Der -Wert für diesen Versuchsausgang ist daher

$P(Y\geq y\mid H_{0})=P(Y\geq 4\mid H_{0})=\sum _{j=0}^{6}{20 \choose j}\left({\frac {1}{2}}\right)^{j}\left(1-{\frac {1}{2}}\right)^{20-j}+\sum _{j=14}^{20}{20 \choose j}\left({\frac {1}{2}}\right)^{j}\left(1-{\frac {1}{2}}\right)^{20-j}$

$={\frac {1}{2^{{20}}}}\sum _{{j=0}}^{{6}}{20 \choose j}+{\frac {1}{2^{{20}}}}\sum _{{j=14}}^{{20}}{20 \choose j}=2{\frac {1}{2^{{20}}}}\sum _{{j=0}}^{{6}}{20 \choose j}\approx 0{,}115$ .

Auf einem Signifikanzniveau von α = 5 % = 0,05 kann man die Nullhypothese nicht verwerfen, da 0,115 > 0,05 (und nicht kleiner, wie nötig wäre). Das heißt, dass man aus den Daten nicht folgern kann, dass die Münze nicht fair ist.

Wäre das Versuchsergebnis k=15 -mal Kopf, also y=5 , dann wäre der -Wert für diesen Versuchsausgang

$P(Y\geq 5\mid H_{0})=2\sum _{{j=0}}^{{5}}{20 \choose j}{\frac {1}{2^{{20}}}}\approx 0{,}041$ .

Auf einem Signifikanzniveau von α = 5 % = 0,05 würde man in diesem Fall die Nullhypothese verwerfen, da 0,041 < 0,05; man würde also schließen, dass die Münze nicht fair ist. Auf einem Signifikanzniveau von 1 % hingegen wären weitere Tests nötig. (Genauer gesagt: Man würde die Datenlage für unzureichend ansehen, um den Schluss zu rechtfertigen, die Münze sei nicht fair. Dies als einen Beweis zu nehmen, dass die Münze fair ist, wäre jedoch falsch.)

Beziehung zum Signifikanzniveau

Es gibt eine Äquivalenz zwischen einem Testverfahren mit der Berechnung des -Wertes und einem Verfahren mit dem im Voraus bestimmten Signifikanzniveau. Der -Wert berechnet sich anhand des beobachteten Wertes der Prüfgröße, und der kritische Wert folgt aus dem Signifikanzniveau $\alpha$ , so gilt z.B. rechtsseitig:

$\!p=P(T\geq t\mid H_{0})$

$\!\alpha =P(T\geq k\mid H_{0})$

und

$p<\alpha \Leftrightarrow t>k,$

KS-Test für die Variable „Mittlerer Hauspreis pro Bezirk“ des Boston-Housing-Datensatzes.

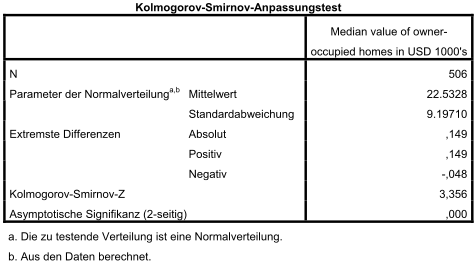
wobei den kritischen Wert darstellt. In statistischer Software wird bei der Durchführung eines Tests der -Wert, siehe rechts unter Asymptotische Signifikanz (letzte Zeile im Kasten), angegeben. Ist der -Wert kleiner als das vorgegebene Signifikanzniveau $\alpha$ , so ist die Nullhypothese abzulehnen.

Auf der einen Seite enthebt die Ausgabe des -Wertes bei einem Test die Software explizit davon, nach dem vorgegebenen Signifikanzniveau zu fragen, um eine Testentscheidung zu treffen. Auf der anderen Seite besteht die Gefahr, dass der Forscher das eigentlich im Voraus festzulegende Signifikanzniveau anpasst, um sein gewünschtes Ergebnis zu bekommen.

Weitere Eigenschaften

Falls die Prüfgröße eine stetige Verteilung hat, ist der -Wert, unter der (punktförmigen) Nullhypothese, uniform verteilt auf dem Intervall [0,1] .

Typische Fehlinterpretationen

Wenn die Nullhypothese zugunsten der Alternativhypothese verworfen wird, wird das Resultat als „statistisch signifikant“ bezeichnet. „Signifikant“ bedeutet hierbei lediglich „überzufällig“. Ein häufiges Missverständnis ist die Gleichsetzung dieser Aussage mit der falschen Behauptung, der -Wert würde angeben, wie wahrscheinlich die Nullhypothese bei Erhalt dieses Stichprobenergebnisses sei. Tatsächlich wird mit dem -Wert jedoch angedeutet, wie extrem das Ergebnis ist: Je kleiner der -Wert, desto mehr spricht das Ergebnis gegen die Nullhypothese.

Goodman formuliert 12 Aussagen über -Werte, die ausgesprochen weit verbreitet und dennoch falsch sind, wie zum Beispiel die folgenden:

Falsch ist: Wenn , ist die Chance, dass die Nullhypothese wahr ist, nur 5 %.
Falsch ist: Ein nicht-signifikanter Unterschied bedeutet bei einem Mittelwertsvergleich zwischen zwei Gruppen, dass die Mittelwerte gleich sind.
Ebenfalls falsch ist: Nur ein signifikanter Unterschied bedeutet, dass das Ergebnis in der Realität, beispielsweise in der klinischen Anwendung, wichtig ist.

Kritik am p-Wert

Kritiker des -Werts weisen darauf hin, dass das Kriterium, mit dem über die „statistische Signifikanz“ entschieden wird, auf einer willkürlichen Festlegung des Signifikanzlevels basiert (oft auf 0,05 gesetzt) und dass das Kriterium zu einer alarmierenden Anzahl von falsch-positiven Tests führt. Der Anteil aller „statistisch signifikanten“ Tests, bei denen die Nullhypothese wahr ist, könnte beträchtlich höher sein als das Signifikanzniveau, was wiederum davon abhängt, wie viele der Nullhypothesen falsch sind und wie hoch die Trennschärfe des Tests ist. Die Einteilung der Resultate in signifikante und nicht-signifikante Ergebnisse kann stark irreführend sein. Zum Beispiel kann die Analyse von beinahe identischen Datensätzen zu -Werten führen, die sich stark in der Signifikanz unterscheiden. In der medizinischen Forschung stellte der -Wert anfangs eine beachtliche Verbesserung der bisherigen Ansätze dar, aber gleichzeitig ist es mit der steigenden Komplexität der publizierten Artikel wichtig geworden, die Fehlinterpretationen des -Werts aufzudecken. Es wurde darauf hingewiesen, dass in Forschungsfeldern wie der Psychologie, bei denen Studien typischerweise eine niedrige Trennschärfe haben, die Anwendung von Signifikanztests zu höheren Fehlerraten führen kann. Die Verwendung von Signifikanztests als Grundlage von Entscheidungen wurde ebenfalls, aufgrund der weit verbreiteten Missverständnisse über den Prozess, kritisiert. Entgegen der weit verbreiteten Meinung gibt der -Wert nicht die Wahrscheinlichkeit der Nullhypothese an, wahr oder falsch zu sein. Des Weiteren sollte die Festlegung der Signifikanzschwelle nicht willkürlich sein, sondern die Konsequenzen eines falsch-positiven Ergebnisses berücksichtigen.

Basierend auf einem Artikel in:

Wikipedia.de