
Kritischer Wert (Statistik)
Ein kritischer Wert ist in der Testtheorie derjenige Schwellenwert, der den Ablehnbereich (synonym: kritischer Bereich) vom Nicht-Ablehnungsbereich trennt. Weitere Details sind im Artikel Statistischer Test benannt.
Beispiel: einseitiger t-Test
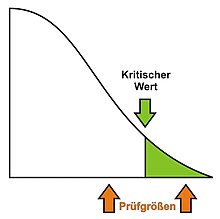
Bei einem einseitigen Einstichproben-t-Test mit dem Ablehnbereich
ist der kritische Wert
das
-Quantil der t-Verteilung mit
Freiheitsgraden. Der kritische Wert ist der Berührungspunkt
zwischen dem Ablehnbereich
und dem Annahmebereich
.
Liegt die Prüfgröße t, das ist eine Realisierung einer Teststatistik T, im Ablehnbereich, ist t also größer als der kritische Wert, so
wird die Nullhypothese dieses
Tests abgelehnt, anderenfalls nicht abgelehnt. Die nebenstehende Abbildung verdeutlicht dies.
Bei einer Testdurchführung, die auf dem p-Wert basiert, ist der p-Wert genau dann kleiner als das vorgegebene
Signifikanzniveau
,
wenn die Prüfgröße t im Ablehnbereich liegt, das bedeutet hier, dass t größer als der kritische Wert ist.
Beispiel: zweiseitiger t-Test
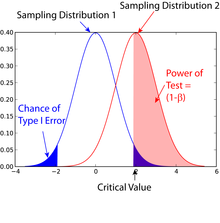
Bei einem zweiseitigen Einstichproben-t-Test setzt sich der Ablehnbereich
aus zwei Teilintervallen zusammen. Dabei bezeichnet
das
-Quantil der t-Verteilung mit
Freiheitsgraden. Es gibt in diesem Fall die zwei kritischen Werte
und
,
die den Ablehnbereich vom Annahmebereich
trennen. Die Nullhypothese dieses Tests wird abgelehnt, wenn die Prüfgröße t im Ablehnbereich liegt, wenn also entweder
oder
gilt.
In der zweiten Abbildung ist, zusammengesetzt aus zwei blauen Teilflächen, die Fehlerwahrscheinlichkeit 1. Art, d. h. die Ablehnwahrscheinlichkeit bei Richtigkeit der Nullhypothese, für den Fall einer zweiseitigen Alternativhypothese dargestellt. Die rot schraffierte Fläche unter der roten Dichtefunktion über dem Ablehnbereich verdeutlicht eine Fehlerwahrscheinlichkeit 2. Art und damit einen Wert der Trennschärfe (Power) des Tests. Ein zweiter, in diesem Fall sehr kleiner, Teil der Fehlerwahrscheinlichkeit 2. Art wird durch die Fläche unter der roten Dichtefunktion über dem linken Teil des Ablehnbereichs beigetragen, ist aber in dieser Graphik nicht sichtbar. Häufig, wie auch in den beiden angegebenen Beispielen von Ablehnbereichen, kann im Fall einer einfachen Nullhypothese der Ablehnbereich so gewählt werden, dass die Fehlerwahrscheinlichkeit 1. Art und das vorgegebene Signifikanzvniveau übereinstimmen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.09. 2023