Trennschärfe eines Tests

Trennschärfe eines Tests beschreibt die Entscheidungsfähigkeit eines statistischen Tests. Andere Ausdrücke hierfür sind Güte, Macht, Power, Schärfe eines Tests, Teststärke oder Testschärfe. Das entsprechende Fachgebiet ist die Testtheorie, ein Teilgebiet der mathematischen Statistik. Im Kontext der Beurteilung eines binären Klassifikators wird die Trennschärfe eines Tests auch als Sensitivität (recall) bezeichnet. Die Trennschärfe eines Tests ist genauso wie das Niveau eines Tests ein Begriff, der aus der Gütefunktion (Trennschärfefunktion) abgeleitet ist.

Die Trennschärfe eines Tests gibt die Fähigkeit eines Tests an, Unterschiede (Effekte) zu erkennen, wenn sie in Wirklichkeit vorhanden sind. Genauer gesagt gibt die Trennschärfe an, mit welcher Wahrscheinlichkeit ein statistischer Test die abzulehnende Nullhypothese $H_{0}$ („Es gibt keinen Unterschied“) korrekt zurückweist, wenn die Alternativhypothese $H_{1}$ („Es gibt einen Unterschied“) wahr ist. Unter der Annahme, dass die Nullhypothese die Abwesenheit einer bestimmten Krankheit („nicht krank“), die Alternativhypothese das Vorhandensein der Krankheit („krank“) und die Ablehnung der Nullhypothese einen positiven diagnostischen Test darstellt, ist die Trennschärfe des Tests äquivalent^[1] zur Sensitivität des Tests (der Wahrscheinlichkeit, dass ein Kranker ein positives Testergebnis aufweist). Zugleich stellt diese Tatsache einen Brückenschlag zwischen der Testtheorie und der Theorie diagnostischen Testens dar.

Die Trennschärfe des Tests kann also als „Ablehnungskraft“ des Tests interpretiert werden. Hohe Trennschärfe des Tests spricht gegen niedrige Trennschärfe für die Nullhypothese $H_{0}$ . Es wird versucht, den Ablehnbereich so zu bestimmen, dass die Wahrscheinlichkeit für die Ablehnung einer „falschen Nullhypothese“ $H_{0}$ , d.h. für Beibehaltung der Alternativhypothese $H_{1}$ unter der Bedingung, dass $H_{1}$ wahr ist, möglichst groß ist: $\operatorname {Pr} (T\in A\mid H_{1})\;=1-\beta$ . Um die Trennschärfe eines Tests berechnen zu können, muss die Alternativhypothese in Form einer konkreten Punkthypothese spezifiziert sein.

Sie bildet das Komplement zur Typ-II-Fehlerwahrscheinlichkeit $\beta$ , d.h. der Wahrscheinlichkeit, bei Gültigkeit von $H_{1}$ fälschlich zugunsten der Nullhypothese ( $H_{0}$ ) zu entscheiden. Die Trennschärfe selbst ist also die Wahrscheinlichkeit, einen ebensolchen Fehler zu vermeiden.

Beschreibung

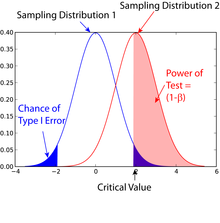
Darstellung der Trennschärfe und des Signifikanzniveaus eines statistischen Tests bei gegebener Nullhypothese (sampling distribution 1) und Alternativhypothese (sampling distribution 2). Eingezeichnet ist ebenso der kritische Wert, der meist durch die Wahl des Signifikanzniveaus festgelegt wird.

Für eine Fehlerwahrscheinlichkeit vom Typ II $\beta$ beträgt die entsprechende Trennschärfe $1-\beta$ . Wenn beispielsweise Experiment E eine Trennschärfe von $0{,}7$ und Experiment F eine Trennschärfe von $0{,}95$ hat, besteht eine höhere Wahrscheinlichkeit, dass Experiment E einen Typ-II-Fehler aufweist als Experiment F, und Experiment F ist, aufgrund seiner geringeren Wahrscheinlichkeit eines Fehlers vom Typ II, zuverlässiger als Experiment E. Äquivalent kann die Trennschärfe eines Tests als die Wahrscheinlichkeit angesehen werden, dass ein statistischer Test die abzulehnende Nullhypothese $H_{0}$ („Es gibt keinen Unterschied“) korrekt zurückweist, wenn die Alternativhypothese $H_{1}$ („Es gibt einen Unterschied“) wahr ist, d.h.

${\text{Trennschärfe}}=\Pr \left({\text{ablehnen}}\;H_{0}\mid H_{1}\;{\text{ist wahr}}\right)=1-\beta$ .

Sie kann also als Fähigkeit eines Tests angesehen werden, einen bestimmten Effekt zu erkennen, wenn dieser bestimmte Effekt tatsächlich vorliegt. Wenn $H_{1}$ keine Gleichheit ist, sondern lediglich die Negation von $H_{0}$ (so hätte man zum Beispiel für $H_{0}:\mu =0$ mit einem nicht beobachtbaren Populationsparameter $\mu$ als Negation einfach $H_{1}:\mu \neq 0$ ), dann kann die Trennschärfe des Tests nicht berechnet werden, es sei denn die Wahrscheinlichkeiten für alle möglichen Werte des Parameters, die die Nullhypothese verletzen sind bekannt. Man bezieht sich also allgemein auf die Trennschärfe eines Tests gegen eine spezifische Alternativhypothese (Punkthypothese).

Mit zunehmender Trennschärfe nimmt die Wahrscheinlichkeit eines Fehlers vom Typ II ab, da die Trennschärfe gleich $1-\beta$ ist. Ein ähnliches Konzept ist die Fehlerwahrscheinlichkeit vom Typ I. Je kleiner bei vorgegebenem Fehler 1. Art $\alpha$ die Wahrscheinlichkeit $\beta$ ist, desto schärfer trennt der Test $H_{0}$ und $H_{1}$ . Ein Test heißt trennscharf, wenn er im Vergleich zu anderen möglichen Tests bei vorgegebenem $\alpha$ eine relativ hohe Trennschärfe aufweist. Wenn $H_{0}$ wahr ist, ist die maximale Trennschärfe eines Tests gleich $\alpha$ .

		H₀ ist wahr	H₁ ist wahr
		Wirklichkeit
Entscheidung des Tests …	… für H₀	Richtige Entscheidung (Spezifität) Wahrscheinlichkeit: 1 - α	Fehler 2. Art Wahrscheinlichkeit: β
Entscheidung des Tests …	… für H₁	Fehler 1. Art Wahrscheinlichkeit: α	richtige Entscheidung Wahrscheinlichkeit: 1-β (Trennschärfe des Tests)

Trennschärfe-Analysen

Trennschärfe-Analysen bzw. Power-Analysen können verwendet werden, um die erforderliche minimale Stichprobengröße zu berechnen, bei der mit hinreichender Wahrscheinlichkeit (Trennschärfe $1-\beta$ ) ein Effekt einer bestimmten Größe (Effektstärke) erkannt werden kann. Beispiel: „Wie oft muss ich eine Münze werfen, um zu dem Schluss zu kommen, dass sie um ein gewisses Ausmaß manipuliert ist?“. Im Kontext der Beurteilung eines binären Klassifikators wird die Trennschärfe eines Tests auch als Sensitivität bezeichnet.

Trennschärfe-Analysen sind in vielen Software-Bibliotheken implementiert, beispielsweise im Python-Paket statsmodels, in der Software G*power und in der statistischen Umgebung R.

Faustregel Stichprobengröße

Die grobe Faustregel von Lehr besagt, dass die Stichprobengröße für einen zweiseitigen Zweistichproben-t-Test mit Trennschärfe 80 % ( $\beta =0{,}2$ ) und Signifikanzniveau $\alpha = 0{,}05$ folgendes gilt:

$n=16{\frac {s^{2}}{\delta ^{2}}},$

wobei $s^{2}$ die (geschätzte) Populationsvarianz ist und $\delta =\mu _{1}-\mu _{2}$ die zu detektierenden Unterschiede der Mittelwerte beider Stichproben. Um die Trennschärfe auf 90 % zu erhöhen muss statt mit 16 mit 21 multipliziert werden. Für einen Einstichproben-t-Test wird 16 mit 8 ersetzt.

Eine intuitive Erklärung ist laut Lehr, dass bei einer Standardnormalverteilung circa 80 % der Fläche unter der Wahrscheinlichkeitsdichte rechts von $z=-0{,}84$ liegt. Daher sollte bei $\beta =20\%$ am kritischen Wert $\delta _{c}=1{,}96S.E.$ folgendes gelten:

$\delta -0{,}84S.E.=\delta _{c}\Leftrightarrow {\frac {\delta -\delta _{c}}{S.E.}}=0{,}84,$

wobei $S.E.={\sqrt {2}}s/{\sqrt {n}}$ der mit ${\sqrt {2}}$ multiplizierte Standardfehler des Mittelwertes ist (wobei der Faktor ${\sqrt {2}}$ auftritt, da die Standardabweichung der Schätzung der Differenz zweier Mittelwerte betrachtet wird). Auflösen nach liefert

$n\approx 15{,}68{\frac {s^{2}}{\delta ^{2}}}\approx 16{\frac {s^{2}}{\delta ^{2}}}.$

Der Wert der Faustregel liegt in der einfachen Form (welche auch nach $\delta$ umgestellt werden kann) und der leichten Merkbarkeit. Bei genauen Aussagen, sollte man eine Trennschärfen-Analyse mit einer Software-Bibliothek durchführen.

Wahl des β-Fehler-Niveaus

Einfluss des Stichprobenumfangs auf die Gütefunktion bzw. Trennschärfe eines einseitigen (in diesem Fall linksseitigen) Tests

Einfluss des Stichprobenumfangs auf die Gütefunktion bzw. Trennschärfe eines zweiseitigen Tests

Für Wirksamkeitsstudien medizinischer Behandlungen schlägt Cohen (1969: 56) für $\beta$ einen 4-mal so hohen Wert wie für das Signifikanzniveau $\alpha$ vor. Wenn $\alpha =5\,\%$ ist, sollte das $\beta$ -Fehler-Niveau also 20 % betragen. Liegt in einer Untersuchung die $\beta$ -Fehler-Wahrscheinlichkeit (Wahrscheinlichkeit für einen Fehler 2. Art) unter dieser 20 %-Grenze, so ist die Trennschärfe ( $1-\beta$ ) damit größer als 80 %.

Es sollte dabei bedacht werden, dass $\beta$ -Fehler bei vorgegebenem, festem Signifikanzniveau $\alpha$ im Allgemeinen nicht direkt kontrolliert werden können. So ist der $\beta$ -Fehler bei vielen asymptotischen oder nichtparametrischen Tests schlechthin unberechenbar oder es existieren nur Simulationsstudien. Bei einigen Tests dagegen, zum Beispiel dem t-Test, kann der $\beta$ -Fehler kontrolliert werden, wenn der statistischen Auswertung eine Stichprobenumfangsplanung vorausgeht.

Ein (aus den Parametern des t-Tests induzierter) Äquivalenztest kann verwendet werden, um den (t-Test) $\beta$ -Fehler unabhängig von der Fallzahlplanung zu kontrollieren. In diesem Fall ist das (t-Test) Signifikanzniveau $\alpha$ variabel.

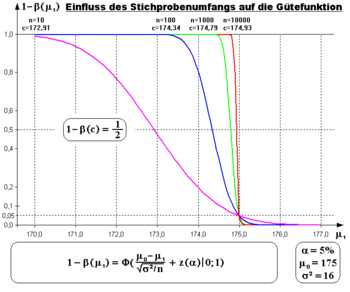
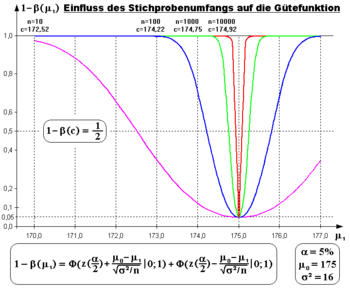
Bestimmungsfaktoren der Trennschärfe

Es gibt verschiedene Möglichkeiten zur Erhöhung der Trennschärfe eines Tests. Die Trennschärfe ( $1-\beta$ ) wird größer:

mit wachsender Differenz von $(\mu _{0}-\mu _{1})$ (das bedeutet: ein großer Unterschied zwischen zwei Teilpopulationen wird seltener übersehen als ein kleiner Unterschied)
mit kleiner werdender Merkmalsstreuung $\sigma$
mit größer werdendem Signifikanzniveau $\alpha$ (sofern $\beta$ nicht festgelegt ist)
mit wachsendem Stichprobenumfang, da der Standardfehler dann kleiner wird: $\sigma _{{\overline {x}}}={\frac {\sigma }{{\sqrt {n}}}}$ . Kleinere Effekte lassen sich durch einen größeren Stichprobenumfang trennen
bei einseitigen Tests im Vergleich zu zweiseitigen Tests: Für den zweiseitigen Test braucht man einen etwa um $25\,\%$ größeren Stichprobenumfang, um dieselbe Trennschärfe wie für den einseitigen Test zu erreichen.
durch die Verwendung des besten bzw. trennschärfsten (englisch most powerful) Tests
durch die Reduktion von Streuung in den Daten, z.B. durch den Einsatz von Filtern oder die Wahl von homogenen Untergruppen (Stratifizierung)
durch die Erhöhung der Empfindlichkeit des Messverfahrens (Verstärken der Effekte, z.B. durch höhere Dosierung)

Wichtig für die Trennschärfe bzw. Power ist auch die Art des statistischen Tests: Parametrische Tests wie zum Beispiel der t-Test haben, falls die Verteilungsannahme stimmt, bei gleichem Stichprobenumfang stets eine höhere Trennschärfe als nichtparametrische Tests wie zum Beispiel der Wilcoxon-Vorzeichen-Rang-Test. Weichen die angenommene und die wahre Verteilung jedoch voneinander ab, liegt also beispielsweise in Wahrheit eine Laplace-Verteilung zugrunde, während eine Normalverteilung angenommen wurde, können nichtparametrische Verfahren jedoch auch eine wesentlich größere Trennschärfe aufweisen als ihre parametrischen Gegenstücke.

Entgegengesetzte Notation

In manchen Quellen wird – was für Verwirrung sorgen kann – für den Fehler 2. Art und die Trennschärfe die genau entgegengesetzte Notation verwendet, also die Wahrscheinlichkeit, einen Fehler 2. Art zu begehen, mit dem Wert $\beta$ .

Literatur

Jacob Cohen: Statistical Power Analysis for the Behavioral Sciences. Erlbaum, Hillsdale, NJ 1969, ISBN 0-8058-0283-5.

Anmerkungen

↑ Dies gilt, da $1-\beta =1-{\frac {f_{\text{n}}}{f_{\text{n}}+r_{\text{p}}}}={\frac {f_{\text{n}}+r_{\text{p}}}{f_{\text{n}}+r_{\text{p}}}}-{\frac {f_{\text{n}}}{f_{\text{n}}+r_{\text{p}}}}={\frac {r_{\text{p}}}{f_{\text{n}}+r_{\text{p}}}}={\text{Sensitivität}}$ . Für die Bedeutung der Notation, siehe Wahrheitsmatrix: Richtige und falsche Klassifikationen.

Basierend auf einem Artikel in:

Wikipedia.de