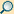Äquivalenztest

Äquivalenztests sind eine Variation von Hypothesentests, mit denen statistische Schlussfolgerungen aus beobachteten Daten gezogen werden können.

In Äquivalenztests wird die Nullhypothese definiert als ein Effekt, der groß genug ist, um als interessant angesehen zu werden, spezifiziert durch eine Äquivalenzgrenze. Die alternative Hypothese ist jeder Effekt, der weniger extrem ist als die gebundene Äquivalenz. Die beobachteten Daten werden statistisch mit den Äquivalenzgrenzen verglichen.

Wenn der statistische Test zeigt, dass die beobachteten Daten überraschend sind, unter der Annahme, dass wahre Effekte mindestens so extrem wie die Äquivalenzgrenzen sind, kann ein Neyman-Pearson-Ansatz für statistische Schlussfolgerungen verwendet werden, um Effektgrößen, die größer als die Äquivalenzgrenzen sind, mit einer im Voraus festgelegten Typ-1-Fehlerrate abzulehnen.

Äquivalenztests können zusätzlich zu Signifikanztests mit Nullhypothese durchgeführt werden. Dies könnte häufige Fehlinterpretationen von p-Werten, die größer als der Alpha-Wert sind, verhindern, um das Fehlen eines wahren Effekts zu unterstützen. Darüber hinaus können Äquivalenztests statistisch signifikante, aber praktisch unbedeutende Effekte identifizieren, wenn die Effekte statistisch von Null verschieden sind, aber auch statistisch kleiner als jede als sinnvoll erachtete Effektgröße (siehe erste Abbildung).

Motivation

Äquivalenztests stammen aus dem Bereich der Pharmakodynami bzw. der Medikamentenentwicklung. Eine Anwendung besteht darin, zu zeigen, dass ein neues Medikament, das billiger ist als verfügbare Alternativen, genauso gut funktioniert wie ein bestehendes Medikament. Im Wesentlichen bestehen Äquivalenztests darin, ein Konfidenzintervall um eine beobachtete Effektgröße herum zu berechnen und Effekte abzulehnen, die extremer sind als die Äquivalenzgrenze, wenn sich das Konfidenzintervall nicht mit der Äquivalenzgrenze überschneidet. Bei zweiseitigen Tests wird eine obere und untere Äquivalenzgrenze angegeben. In Nicht-Unterlegenheitsstudien, in denen das Ziel darin besteht, die Hypothese zu testen, dass eine neue Behandlung nicht schlechter ist als bestehende Behandlungen, ist nur eine niedrigere Äquivalenzgrenze im Voraus festgelegt.

Mittlere Differenzen (schwarze Quadrate) und 90 % Konfidenzintervalle (horizontale Linien) mit Äquivalenzgrenzen ΔL = −0,5 und ΔU= 0,5 für vier Kombinationen von Testergebnissen, die statistisch äquivalent sind oder nicht und sich statistisch von Null oder nicht unterscheiden. Das Muster A ist statistisch äquivalent, das Muster B ist statistisch verschieden von 0, das Muster C ist praktisch unbedeutend und das Muster D ist nicht schlüssig (weder statistisch verschieden von 0 noch äquivalent).

TOST-Verfahren

Ein sehr einfacher Äquivalenztestansatz ist das Verfahren der „zwei einseitigen t-Tests“ (englisch two one sided tests, kurz: TOST). Im TOST-Verfahren wird eine obere (Δ_U) und eine untere (–Δ_L) Äquivalenzgrenze basierend auf der kleinsten Effektgröße von Interesse (z.B. eine positive oder negative Differenz von d = 0,3) angegeben. Zwei zusammengesetzte Nullhypothesen werden getestet: H₀₁: Δ ≤ -Δ_L und H₀₂: Δ ≥ Δ_U. Wenn beide einseitigen Tests statistisch abgelehnt werden können, können wir zu dem Schluss kommen, dass -Δ_L < Δ < Δ_U, oder dass der beobachtete Effekt innerhalb der Äquivalenzgrenzen liegt und statistisch kleiner ist als jeder als sinnvoll erachtete und praktisch gleichwertige Effekt. Alternativen zum TOST-Verfahren wurden ebenfalls entwickelt. Eine erfolgte Modifikation von TOST macht den Ansatz bei wiederholten Messungen und der Bewertung mehrerer Variablen möglich.

Bootstrap-Test

Bootstrap-Tests können die Nullhypothese $H_{0}:F\neq G$ testen und sind somit für Äquivalenztests geeignet.

Vergleich zwischen t-Test und Äquivalenztest

Der Äquivalenztest kann zu Vergleichszwecken aus dem t-Test „induziert“ werden. Bei einem t-Test zum Signifikanzniveau α_t-Test und welcher für eine Effektgröße d_r eine Power von 1-β_t-Test erreicht, führen beide Tests zu der gleichen Schlussfolgerung, wenn die Parameter Δ=d_r sowie α_equiv.-test=β_t-test und β_equiv.-test=α_t-test zusammenfallen, d.h. die Fehler (Typ I und Typ II) zwischen dem t-Test und dem Äquivalenztest sind vertauscht. Um dies für den t-Test zu gewährleisten, muss entweder die Fallzahlplanung korrekt durchgeführt werden oder durch Anpassung des Signifikanzniveaus α_t-test ein korrigierter Test bestimmt werden. Beide Ansätze haben praktische Probleme, da die Fallzahlplanung auf nicht überprüfbaren Annahmen hinsichtlich der Standardabweichung beruht und beim Anpassen von α_t-test (sogenannter revised t-Test) numerische Probleme auftreten. Diese Einschränkungen treten bei Anwendung des Äquivalenztests nicht auf.

Die zweite Abbildung ermöglicht einen Vergleich des Äquivalenztests und des t-Tests, wenn die Fallzahlplanung von Differenzen zwischen der A-priori-Standardabweichung ${\textstyle \sigma }$ und der Standardabweichung aus der Stichprobe ${\textstyle {\hat {\sigma }}}$ betroffen ist. Die Verwendung eines Äquivalenztests anstelle eines t-Tests stellt sicher, dass α_equiv.-test (bzw. β_t-test) beschränkt ist, was der t-Test nicht tut. Insbesondere im Fall ${\textstyle {\hat {\sigma }}>\sigma }$ kann im t-Test der Typ II Fehler beliebig groß werden. Demgegenüber führt ${\textstyle {\hat {\sigma }}<\sigma }$ dazu, dass der t-Test strenger ausfällt als der für d_r geplante, was zu zufälligen Nachteilen (z.B. eines Geräteherstellers) führen kann. Dies macht den Äquivalenztest sicherer in der Anwendung.

Wahrscheinlichkeit, den t-Test (a) bzw. den Äquivalenztest (b) zu bestehen, abhängig vom tatsächlichen Fehler 𝜇

Weiterführende Literatur

Esteban Walker, Amy S. Nowacki: Understanding Equivalence and Noninferiority Testing. In: Journal of General Internal Medicine. 26. Jahrgang, Februar 2011, S. 192–6, PMC 3019319 (freier Volltext).

Basierend auf einem Artikel in:

Wikipedia.de