Einstichproben-t-Test

Der Einstichproben-t-Test (engl. one sample t-test) ist ein Signifikanztest aus der mathematischen Statistik. Er prüft anhand des Mittelwertes einer Stichprobe, ob der Mittelwert einer Grundgesamtheit gleich einem vorgegebenen Wert ist (bzw. kleiner oder größer).

Eine entsprechende Erweiterung eines Mittelwertvergleiches für zwei (abhängige oder unabhängige) Stichproben ist der Zweistichproben-t-Test.

Testidee

Der Einstichproben-t-Test prüft (im einfachsten Fall) mit Hilfe des Mittelwertes ${\bar {x}}$ einer Stichprobe, ob der Mittelwert der Grundgesamtheit $\mu$ verschieden von einem vorgegebenen Wert $\mu _{0}$ ist.

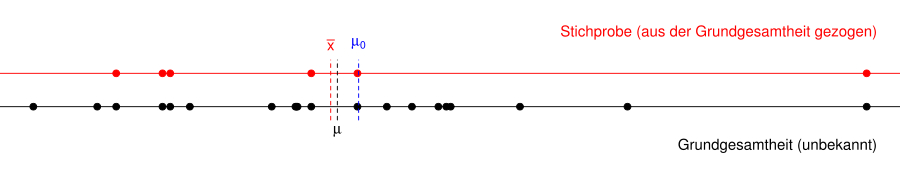
Die untenstehende Grafik zeigt eine Grundgesamtheit (schwarze Punkte) und eine Stichprobe (rote Punkte), die zufällig aus der Grundgesamtheit gezogen wurde. Der Mittelwert ${\bar {x}}$ der Stichprobe kann aus der Stichprobe berechnet werden, der Mittelwert $\mu$ der Grundgesamtheit ist jedoch unbekannt. Man vermutet, z.B. wegen historischer Ergebnisse oder theoretischer Überlegungen, dass der Mittelwert $\mu$ der Grundgesamtheit verschieden von einem vorgegebenen Wert $\mu _{0}$ ist.

Im einfachsten Fall prüft der Test

die Nullhypothese, dass der Mittelwert der Grundgesamtheit gleich dem vorgegebenen Wert ist ( $H_0:\,\mu=\mu_0$ )
gegen die Alternativhypothese, dass der Mittelwert der Grundgesamtheit ungleich dem vorgegebenen Wert ist ( $H_1:\,\mu\neq\mu_0$ ).

Wenn die Stichprobe geeignet gezogen wird, z.B. als einfache Zufallsstichprobe, wird der Mittelwert der Stichprobe ${\bar {x}}$ mit hoher Wahrscheinlichkeit nahe bei dem Mittelwert der Grundgesamtheit $\mu$ liegen. D.h. der Abstand zwischen der gestrichelten roten und schwarzen Linie wird mit hoher Wahrscheinlichkeit klein sein.

Liegt nun der vorgegebene Wert $\mu _{0}$ nahe dem Mittelwert der Stichprobe ${\bar {x}}$ , d.h. die gestrichelte blaue und die gestrichelte rote Linie haben einen kleinen Abstand, dann liegt der vorgegebene Wert $\mu _{0}$ auch nahe dem Mittelwert der Grundgesamtheit $\mu$ . Wir können dann die Nullhypothese nicht ablehnen.
Liegt jedoch der vorgegebene Wert $\mu _{0}$ weit entfernt von dem Mittelwert der Stichprobe ${\bar {x}}$ , d.h. die gestrichelte blaue und die gestrichelte rote Linie haben einen großen Abstand, dann liegt der vorgegebene Wert $\mu _{0}$ auch weit entfernt von dem Mittelwert der Grundgesamtheit $\mu$ . Dann können wir die Nullhypothese ablehnen.

Die genauen mathematischen Berechnungen finden sich in den folgenden Abschnitten.

Hypothesen

Für den Einstichproben-t-Test können drei verschiedene Hypothesenpaare (Nullhypothese $H_{0}$ vs. Alternativhypothese $H_{1}$ ) formuliert werden:

$H_0:\,\mu=\mu_0$ vs. $H_1:\,\mu\neq\mu_0$ (zweiseitiger Test),
$H_0:\,\mu\leq\mu_0$ vs. $H_1:\,\mu>\mu_0$ (rechtsseitiger Test) und
$H_0:\,\mu\geq\mu_0$ vs. $H_1:\,\mu<\mu_0$ (linksseitiger Test),

Für alle drei Hypothesenpaare wird die gleiche Teststatistik benutzt, lediglich die Bereiche für die Ablehnung bzw. Annahme der Nullhypothese unterscheiden sich.

Mathematische Herleitung der Teststatistik

Für eine normalverteilte Grundgesamtheit

Sind $X_1, X_2, \dots, X_n$ unabhängige normalverteilte Zufallsvariablen mit Erwartungswert $\mu \in \mathbb {R}$ und Standardabweichung $\sigma >0$ , und möchte man die Nullhypothese $\mu=\mu_0$ testen, dann liegt es nahe, ihr arithmetisches Mittel

$\bar X = \frac{1}{n} \sum_{i=1}^n X_i$

als Teststatistik zu benutzen. Sie ist namentlich ebenfalls normalverteilt mit Erwartungswert $\mu$ , hat aber die Standardabweichung ${\tfrac {\sigma }{{\sqrt {n}}}}$ . Bei bekanntem $\sigma$ könnte die Hypothese mit einem Gauß-Test getestet werden. Dazu berechnet man

$Z = \sqrt{n}\frac{\bar X - \mu_0}{\sigma}$ ,

welche unter der Nullhypothese standardnormalverteilt ist.

Normalerweise ist jedoch die Standardabweichung unbekannt und tritt (da man hier keine Inferenz über $\sigma$ betreibt) hier als sogenannter Störparameter auf. In diesem Fall liegt es nahe, sie durch die empirische Standardabweichung

$S = \sqrt{\frac{\sum_{i=1}^n(X_i - \bar X )^2}{n-1}}$

zu schätzen und als Teststatistik

$T = \sqrt{n}\frac{\bar X - \mu_0}{S}$

zu verwenden. Diese Statistik ist unter der Nullhypothese allerdings nicht mehr normalverteilt, sondern t-verteilt mit n-1 Freiheitsgraden. Ist der Wert der Teststatistik für eine konkrete Stichprobe so groß (oder so klein), dass dieser oder ein noch signifikanterer Wert unter der Nullhypothese hinreichend unwahrscheinlich ist, wird die Nullhypothese abgelehnt.

Für eine beliebig verteilte Grundgesamtheit

Sind $X_1, X_2, \dots, X_n$ ( n>30 ) unabhängig und identisch verteilte Zufallsvariablen mit Erwartungswert $\mu \in \mathbb {R}$ und Standardabweichung $\sigma >0$ , dann liegt es wie im obigen Fall nahe, ihr arithmetisches Mittel

$\bar X = \frac{1}{n} \sum_{i=1}^n X_i$

als Teststatistik zu benutzen. Obwohl die Verteilung von ${\bar {X}}$ unbekannt ist, gilt aufgrund des zentralen Grenzwertsatzes, dass es approximativ normalverteilt ist mit Erwartungswert $\mu$ und Standardabweichung ${\tfrac {\sigma }{{\sqrt {n}}}}$ .

Weil normalerweise die Standardabweichung unbekannt ist, liegt es auch in diesem Fall nahe, sie durch die empirische Standardabweichung

$S = \sqrt{\frac{\sum_{i=1}^n(X_i - \bar X )^2}{n-1}}$

zu schätzen und wieder als Teststatistik

$T = \sqrt{n}\frac{\bar X - \mu_0}{S}$

zu verwenden. Diese Statistik ist unter der Nullhypothese allerdings nur annähernd t-verteilt mit n-1 Freiheitsgraden. Ist der Wert der Teststatistik für eine konkrete Stichprobe so groß (oder so klein), dass dieser oder ein noch extremerer Wert unter der Nullhypothese hinreichend unwahrscheinlich ist, wird die Nullhypothese abgelehnt.

Beispiel

Zweiseitiger Test

Es soll getestet werden, ob die durchschnittliche Laufzeit $\mu$ von Notebook-Akkus möglicherweise von den vom Hersteller angegebenen 3,5 Stunden abweicht. Dazu werden bei 10 Akkus dieser Marke unter kontrollierten gleichen Bedingungen die Laufzeiten gemessen. Da wir nur wenige Beobachtungen haben, kann der zentrale Grenzwertsatz nicht angewendet werden; siehe Abschnitt Mathematische Herleitung der Teststatistik für eine beliebig verteilte Grundgesamtheit. Wir müssen daher davon ausgehen, dass die Laufzeit der Notebook-Akkus in der Grundgesamtheit normalverteilt ist.

Folgende Hypothesen sollen geprüft werden:

Allgemein	Beispiel
$H_0:\, \mu = \mu_0$ vs. $H_1:\, \mu \neq \mu_0$	$H_0:\, \mu = 3{,}5$ Stunden vs. $H_1:\, \mu \neq 3{,}5$ Stunden

Bei der Durchführung des Tests ergebe sich beispielsweise der Stichprobenmittelwert $\bar{x} = 3{,}25$ Stunden und die Stichprobenstandardabweichung s = 0{,}31 Stunden. Daraus lässt sich nun der Prüfwert folgendermaßen berechnen:

Allgemein	Beispiel
$t = \sqrt{n}\frac{\bar x - \mu_0}{s}$	$t = \sqrt{10}\frac{3{,}25-3{,}5}{0{,}31} \approx -2{,}55$
mit $\bar x = \frac{1}{n}\sum_{i=1}^n x_i$	$\bar{x}=3{,}25$ Stunden
und $s = \sqrt{\frac{\sum_{i=1}^n(x_i-\bar x)^2}{n-1}}$	Stunden

Die Nullhypothese wird zum Signifikanzniveau $\alpha$ abgelehnt, falls $|t| > t(1-\tfrac{\alpha}{2}, n-1)$ . Darin entspricht $t(1-\tfrac{\alpha}{2}, n-1)$ dem $(1 - \tfrac{\alpha}{2})$ -Quantil der t-Verteilung mit n-1 Freiheitsgraden.

Für das Beispiel heißt das, dass die Nullhypothese abgelehnt wird bei einem Signifikanzniveau $\alpha =5\,\%$ , wenn t kleiner ist als das 2,5 %-Quantil oder größer als das 97,5 %-Quantil der t-Verteilung mit 10-1=9 Freiheitsgraden. Man findet mit Hilfe einer t-Tabelle oder eines Computerprogramms den Wert t(0{,}975; 9) = 2{,}262 . Aufgrund der Symmetrie der t-Verteilung ist t(0{,}025; 9) = -2{,}262 . Wegen $t=-2{,}55<-2{,}262$ kann die Nullhypothese, dass der Erwartungswert der Laufzeit gleich 3,5 Stunden ist, zum Signifikanzniveau $\alpha =5\,\%$ abgelehnt werden. Die Akkus laufen im Mittel nicht 3,5 Stunden, also mehr oder weniger.

Einseitiger Test

In der Praxis hätte man einen einseitigen Test durchgeführt, denn nur wenn die Akkus mehr als 3,5 Stunden laufen, dann ist man als Kunde zufrieden. Die Hypothesen zum Prüfen, ob die Akkus mindestens 3,5 Stunden durchhalten, lauten dann

Allgemein	Beispiel
$H_0:\, \mu \geq \mu_0$ vs. $H_1:\, \mu < \mu_0$	$H_0:\, \mu \geq 3{,}5$ Stunden vs. $H_1:\, \mu < 3{,}5$ Stunden

Der Prüfwert ergibt sich wieder zu $t \approx -2{,}55$ und kann auch zum Testen der einseitigen Hypothese zum Signifikanzniveau $\alpha$ verwendet werden. Die Nullhypothese $\mu \geq \mu_0$ wird nun abgelehnt, wenn $t < -t(1-\alpha,\ n-1)$ ist.

Für $\alpha = 0{,}05$ ergibt sich $t(1-\alpha,\ n-1)=1{,}833$ . Und da -2{,}55<-1{,}833 gilt, können wir diese Nullhypothese ebenfalls ablehnen, d.h., wir konnten zeigen, dass die durchschnittliche Akkulaufzeit kleiner als 3,5 Stunden ist.

Alternative Tests

Im Fall,

wenn der zentrale Grenzwertsatz für die Stichprobenvariablen $X_{i}$ nicht erfüllt ist oder
wenn der zentrale Grenzwertsatz für die Stichprobenvariablen $X_{i}$ erfüllt ist und der Stichprobenumfang kleiner gleich 30 ist

kann als Alternative der nichtparametrische Einstichproben-Median-Test eingesetzt werden. Dieser testet allerdings, ob der Median der Grundgesamtheit einem vorgegebenen Wert entspricht.

Ist die Standardabweichung $\sigma$ bekannt, dann sollte der Einstichproben-Gauß-Test verwendet werden.

Kompaktdarstellung

Einstichproben-t-Test
Voraussetzungen	$X_i\,$ unabhängig voneinander $X_{i}\sim {\mathcal {N}}(\mu ;\sigma )\,$ oder $X_i\sim (\mu;\sigma)\,$ und hinreichend großes (siehe ZGS)
Hypothesen	$H_0: \mu\leq\mu_0$ $H_1: \mu>\mu_0\,$ (rechtsseitig)	$H_0: \mu=\mu_0\,$ $H_1: \mu\neq\mu_0$ (zweiseitig)	$H_0: \mu\geq\mu_0$ $H_1: \mu<\mu_0\,$ (linksseitig)
Teststatistik	$T=\sqrt{n}\frac{\bar{X}-\mu_0}{S} \sim t_{n-1}$
Prüfwert	$t=\sqrt{n}\frac{\bar{x}-\mu_0}{s}$ mit $\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i$ und $s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2}$
Ablehnungsbereich $H_{0}$	$(t_{1-\alpha;n-1},\infty)\,$	$(-\infty,-t_{1-\frac{\alpha}2;n-1})\cup (t_{1-\frac{\alpha}2;n-1},\infty)\,$	$(-\infty,-t_{1-\alpha;n-1})\,$

Basierend auf einem Artikel in:

Wikipedia.de