Orthogonalprojektion
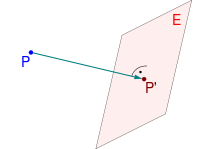
Eine Orthogonalprojektion (von gr. ὀρθός orthós gerade, γωνία gōnía Winkel und lat. prōicere, PPP prōiectum vorwärtswerfen), orthogonale Projektion oder senkrechte Projektion ist eine Abbildung, die in vielen Bereichen der Mathematik eingesetzt wird. In der Geometrie ist eine Orthogonalprojektion die Abbildung eines Punkts auf eine Gerade oder eine Ebene, sodass die Verbindungslinie zwischen dem Punkt und seinem Abbild mit dieser Gerade oder Ebene einen rechten Winkel bildet. Das Abbild hat dann von allen Punkten der Gerade oder Ebene den kürzesten Abstand zum Ausgangspunkt. Eine Orthogonalprojektion ist damit ein Spezialfall einer Parallelprojektion, bei der die Projektionsrichtung gleich der Normalenrichtung der Gerade oder Ebene ist.
In der linearen Algebra wird dieses Konzept auf höherdimensionale Vektorräume über den reellen oder komplexen Zahlen und allgemeinere Winkel- und Abstandsbegriffe erweitert. Eine Orthogonalprojektion ist dann die Projektion eines Vektors auf einen Untervektorraum, sodass der Differenzvektor aus Abbild und Ausgangsvektor in dessen orthogonalem Komplement liegt. In der Funktionalanalysis wird der Begriff noch weiter in unendlichdimensionalen Skalarprodukträumen gefasst und insbesondere auf Funktionen angewandt. Die Existenz und Eindeutigkeit solcher Orthogonalprojektionen stellt dann der Projektionssatz sicher.
Orthogonalprojektionen besitzen vielfältige Einsatzbereiche innerhalb der Mathematik, beispielsweise in der darstellenden Geometrie, dem Gram-Schmidtschen Orthogonalisierungsverfahren, der Methode der kleinsten Quadrate, dem Verfahren der konjugierten Gradienten, der Fourier-Analysis oder der Bestapproximation. Sie besitzen Anwendungen unter anderem in der Kartografie, der Architektur, der Computergrafik und der Physik.
Darstellende Geometrie
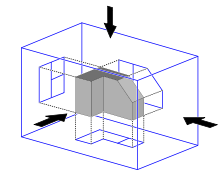
In der darstellenden Geometrie und im technischen Zeichnen dienen Projektionen dazu, zweidimensionale Abbildungen von dreidimensionalen geometrischen Körpern herzustellen. Neben der Zentralprojektion kommen hierbei häufig Parallelprojektionen zum Einsatz. Eine Parallelprojektion ist eine Abbildung, die Punkte des dreidimensionalen Raums auf Punkte einer gegebenen Bildebene abbildet, wobei die Projektionsstrahlen zueinander parallel sind. Treffen die Projektionsstrahlen im rechten Winkel auf die Projektionsebene, so spricht man von einer Orthogonalprojektion.
Werden statt einer Bildebene drei Projektionsebenen verwendet, die
aufeinander senkrecht
stehen, dann handelt es sich um eine Dreitafelprojektion oder Normalprojektion.
Meist liegen dabei die Projektionsebenen parallel zu den Achsen des verwendeten
(kartesischen) Koordinatensystems.
Besitzt ein Punkt im Raum dann die Koordinaten ,
so erhält man die Orthogonalprojektionen des Punkts auf die drei Koordinatenebenen
durch
(Projektion auf die xy-Ebene)
(Projektion auf die xz-Ebene)
(Projektion auf die yz-Ebene)
Verläuft eine Projektionsebene zwar parallel zu zwei der Koordinatenachsen,
aber nicht durch den Nullpunkt des Koordinatensystems, so erhält man den
projizierten Punkt durch Ersetzen des Werts
durch den Schnittpunkt
der Ebene mit der dritten Koordinatenachse. Bei einer orthogonalen Axonometrie, beispielsweise
einer Isometrie
oder einer Dimetrie,
wird das abzubildende Objekt vor der Projektion auf spezifische Weise gedreht.
Analytische Geometrie
Die analytische Geometrie beschäftigt sich mit der Berechnung und den mathematischen Eigenschaften von Orthogonalprojektionen im zwei- und dreidimensionalen Raum, insbesondere für den Fall, dass die Projektionsebene nicht parallel zu den Koordinatenachsen liegt.
Projektion auf eine Gerade
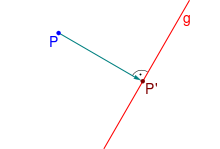
Definition
In der euklidischen
Ebene ist eine Orthogonalprojektion die Abbildung eines
Punkts
auf eine Gerade
,
derart dass die Verbindungslinie zwischen dem Punkt und seinem Abbild
einen rechten Winkel mit der Gerade bildet. Eine Orthogonalprojektion muss
demnach die beiden Bedingungen
(Projektion)
(Orthogonalität)
erfüllen. Die Linie
heißt Lot
des Punkts auf die Gerade und der projizierte Punkt
wird Lotfußpunkt genannt. Die zeichnerische
Konstruktion des Lots mit Zirkel und Lineal ist eine Standardaufgabe der euklidischen
Geometrie und man spricht dabei vom Fällen
des Lots.
Herleitung
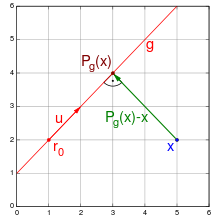
In der analytischen Geometrie werden Punkte im kartesischen
Koordinatensystem durch Ortsvektoren
beschrieben und Geraden typischerweise als Geradengleichung
in Parameterform
,
wobei
der Ortsvektor eines Geradenpunkts,
der Richtungsvektor der Geraden und
ein reeller Parameter
ist. Zwei Vektoren
und
bilden dabei einen rechten Winkel, wenn ihr Skalarprodukt
ist. Die Orthogonalprojektion
auf die Gerade
muss die beiden Bedingungen
für ein
erfüllen.
Wird die erste Gleichung in die zweite eingesetzt, so erhält man
,
was nach
aufgelöst
ergibt.
Verläuft die Gerade als Ursprungsgerade
durch den Nullpunkt,
dann gilt
und die Formel vereinfacht sich zu
.
Ist zudem der Richtungsvektor der Gerade ein Einheitsvektor,
gilt also ,
so erhält man die einfachere Darstellung
.
Der Faktor
gibt dann an, wie weit der projizierte Punkt auf der Gerade vom Nullpunkt
entfernt ist. Analog kann auch ein Punkt
im euklidischen
Raum auf eine Gerade im Raum orthogonal projiziert werden, es wird lediglich
mit drei statt zwei Komponenten gerechnet.
Beispiele
Die Orthogonalprojektion des Punkts mit
auf die Ursprungsgerade mit Richtung
in der euklidischen Ebene ist
.
Die Orthogonalprojektion des Punkts mit
auf die Ursprungsgerade mit Richtung
im euklidischen Raum ist
.
Eigenschaften
Befindet sich der zu projizierende Punkt
bereits auf der Gerade, dann gibt es eine Zahl
mit
und die Orthogonalprojektion
verändert den Punkt nicht. Andernfalls minimiert die Orthogonalprojektion den Abstand zwischen dem Ausgangspunkt und allen Geradenpunkten, da für das Quadrat dieses Abstands nach dem Satz des Pythagoras
für alle Zahlen
gilt. Das Minimum wird dabei eindeutig an dem orthogonal projizierten Punkt
angenommen, da der erste Term der Summe genau für
null wird. Bilden die Vektoren
und
einen rechten Winkel, so ist der projizierte Punkt der Nullpunkt.
Berechnung
Die Orthogonalprojektion eines Punkts
auf eine Gerade
,
die keine Ursprungsgerade ist, ist durch
.
gegeben, was durch Einsetzen der allgemeinen Geradengleichung in die
Orthogonalitätsbedingung und durch Auflösen nach dem freien Parameter
ermittelt werden kann. Aus dem Allgemeinfall erhält man die obigen Spezialfälle,
indem der Stützvektor
der Gerade in den Nullpunkt verschoben
wird und ihr Richtungsvektor normiert
wird, also durch seinen Betrag
geteilt wird. In dem Beispiel der obigen Abbildung ist
,
sowie
und damit
.
Alternativ kann eine Orthogonalprojektion im zweidimensionalen Fall auch
durch Ermittlung des Schnittpunkts der Ausgangsgeraden mit der Lotgeraden
berechnet werden. Ist
ein Normalenvektor
der Ausgangsgeraden, so folgt aus den beiden Bedingungen
durch Einsetzen der ersten Gleichung in die zweite Gleichung und Auflösen
nach dem freien Parameter
für die Orthogonalprojektion
.
Einen Normalenvektor kann man durch Vertauschen der beiden Komponenten des
Richtungsvektors der Geraden und durch Umkehrung des Vorzeichens einer der
beiden Komponenten ermitteln. In dem obigen Beispiel ist ein solches .
Da eine Gerade im dreidimensionalen Raum keine ausgezeichnete Normalenrichtung
besitzt, ist dieser einfache Ansatz aber nur in zwei Dimensionen möglich.
Projektion auf eine Ebene
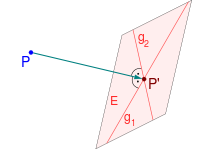
Definition
Im dreidimensionalen Raum kann ein Punkt
auch auf eine Ebene
orthogonal projiziert werden. Eine Orthogonalprojektion muss dann die beiden
Bedingungen
(Projektion)
(Orthogonalität)
erfüllen. Auch hier spricht man von Lot und Lotfußpunkt. Die Orthogonalität
impliziert dabei, dass das Lot senkrecht auf allen Geraden der Ebene durch den
Lotfußpunkt
steht.
Herleitung
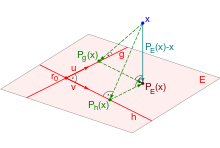
Ein Punkt im euklidischen Raum werde wieder durch einen Ortsvektor
Aufgrund der Linearität des Skalarprodukts reicht es dabei aus, Orthogonalität bezüglich der beiden Spannvektoren statt bezüglich aller Vektoren der Ebene nachzuweisen.
Handelt es sich bei der Ebene um eine Ursprungsebene,
das heißt ,
dann muss die Orthogonalprojektion
des Punkts
auf die Ebene
die folgenden drei Bedingungen erfüllen:
Setzt man die erste Gleichung in die anderen beiden Gleichungen ein, erhält man mit
ein lineares
Gleichungssystem mit zwei Gleichungen und den beiden Unbekannten
und
.
Falls die Spannvektoren zueinander orthogonal
sind, das heißt
gilt, dann zerfällt dieses Gleichungssystem in zwei voneinander unabhängige
Gleichungen und seine Lösung kann direkt angegeben werden. Die
Orthogonalprojektion
des Punkts
auf die Ebene
ist dann gegeben durch:
Sind die Spannvektoren sogar orthonormal,
gilt also zusätzlich ,
dann hat man die einfachere Darstellung
-
.
Man erhält die Orthogonalprojektion eines Punkts auf eine Ebene also durch
Ermittlung der Orthogonalprojektionen
und
des Punkts auf die beiden von den Spannvektoren gebildeten Geraden
und
und durch Addition der Resultate (siehe Abbildung).
Beispiel
Die Orthogonalprojektion des Punkts
auf die Ursprungsebene, die durch die orthogonalen Vektoren
und
aufgespannt wird, ist
.
Eigenschaften
Befindet sich der zu projizierende Punkt
bereits auf der Ebene, dann gibt es Zahlen
und
mit
und die Orthogonalprojektion
verändert den Punkt nicht. Andernfalls minimiert der orthogonal projizierte Punkt den Abstand zwischen dem Ausgangspunkt und allen Punkten der Ebene, da für das Quadrat dieses Abstands mit dem Satz des Pythagoras
für alle Zahlen
gilt. Das Minimum wird dabei eindeutig für
und
an dem orthogonal projizierten Punkt angenommen. Bildet
sowohl mit
,
als auch mit
einen rechten Winkel, dann ist der projizierte Punkt der Nullpunkt.
Berechnung
Verläuft eine Ebene nicht durch den Ursprung, so kann sie durch Translation
um
in den Ursprung verschoben werden. Sind ihre Spannvektoren nicht orthogonal, so
können diese mit Hilfe des Gram-Schmidtschen
Orthogonalisierungsverfahrens orthogonalisiert werden. Hierzu ermittelt man
(beispielsweise) einen zu
orthogonalen Vektor
als Verbindungsvektor von
zur Orthogonalprojektion von
auf die Gerade in Richtung
und erhält somit den Allgemeinfall einer Orthogonalprojektion eines Punkts
auf eine Ebene
durch
.
Alternativ dazu kann eine Orthogonalprojektion auch durch Berechnung des
Schnitts der Lotgeraden mit der Ebene berechnet werden. Ein Normalenvektor
der Ebene kann, sofern sie nicht in Normalenform
gegeben ist, über das Kreuzprodukt
der (nicht notwendigerweise orthogonalen, aber nichtkollinearen) Spannvektoren
durch
berechnet werden. Man erhält dann wie im zweidimensionalen Fall als
Orthogonalprojektion
.
Lineare Algebra
In der linearen
Algebra wird das Konzept der Orthogonalprojektion auf allgemeine Vektorräume
mit endlicher Dimension
über dem Körper
der reellen oder komplexen Zahlen, sowie
allgemeine
Skalarprodukte
und damit Orthogonalitätsbegriffe
verallgemeinert. Zwei Vektoren
sind definitionsgemäß genau dann orthogonal, wenn ihr Skalarprodukt
ist.[1]
Algebraische Darstellung
Definition
Eine Orthogonalprojektion auf einen Untervektorraum
eines Vektorraums
ist eine lineare
Abbildung
,
die für alle Vektoren
die beiden Eigenschaften
(Projektion)
für alle
(Orthogonalität)[2]
erfüllt. Der Differenzvektor
liegt damit im orthogonalen
Komplement
von
.
Das orthogonale Komplement ist selbst ein Untervektorraum bestehend aus
denjenigen Vektoren in
,
die orthogonal zu allen Vektoren in
sind.
Darstellung
Ist
eine Basis
des Untervektorraums
mit der Dimension
,
dann hat jeder Vektor
eine eindeutige Darstellung als Linearkombination
.
Aufgrund der Sesquilinearität
des Skalarprodukts reicht es daher aus, Orthogonalität lediglich bezüglich der
Basisvektoren statt bezüglich aller Vektoren des Untervektorraums nachzuweisen.
Eine Orthogonalprojektion
muss demnach die Bedingungen
für
erfüllen. Setzt man die erste Gleichung in die anderen Gleichungen ein, erhält man mit
für
ein lineares Gleichungssystem mit
Gleichungen und den
Unbekannten
.
Die dabei zugrunde liegende Gramsche
Matrix
ist aufgrund der linearen
Unabhängigkeit der Basisvektoren regulär
und damit ist dieses Gleichungssystem eindeutig lösbar. Ist nun
eine Orthogonalbasis
von
,
das heißt
für
,
dann ist die zugehörige Gramsche Matrix eine Diagonalmatrix
und das Gleichungssystem hat eine direkt angebbare Lösung. Die
Orthogonalprojektion
des Vektors
auf den Untervektorraum
ist dann durch
gegeben. Bildet
sogar eine Orthonormalbasis,
das heißt
mit dem Kronecker-Delta
,
dann hat die Orthogonalprojektion die einfachere Darstellung
.
Beispiele
Wählt man als Vektorraum
den Standardraum
und als Skalarprodukt
das Standardskalarprodukt,
so ist ein Untervektorraum eine lineare
Mannigfaltigkeit (etwa eine Gerade, Ebene oder Hyperebene)
durch den Nullpunkt und die Orthogonalprojektionen des vorangegangenen
Geometrie-Abschnitts entsprechen gerade den Spezialfällen
- Projektion auf eine Ursprungsgerade in der Ebene:
- Projektion auf eine Ursprungsgerade im Raum:
- Projektion auf eine Ursprungsebene im Raum:
Der Fall
entspricht in jeder Dimension der Abbildung eines Vektors auf den Nullpunkt und
der Fall
lässt den Vektor immer unverändert, da eine Orthogonalprojektion dann die identische
Abbildung ist.
Eigenschaften
Eine Orthogonalprojektion ist eine Projektion,
das heißt eine idempotente
lineare Abbildung des Vektorraumes
in sich selbst (genannt Endomorphismus).
Ist der zu projizierende Vektor
nämlich bereits Element des Untervektorraums, dann gibt es Skalare
,
sodass
ist, und die Orthogonalprojektion
verändert den Vektor nicht, woraus die Idempotenz folgt. Die Linearität der Abbildung folgt direkt aus der Sesquilinearität des Skalarprodukts. Zudem gilt die Selbstadjungiertheit
für alle Vektoren .
Der orthogonal projizierte Vektor minimiert den Abstand
zwischen dem Ausgangsvektor und allen Vektoren des Untervektorraums bezüglich
der von dem Skalarprodukt abgeleiteten
Norm
,
denn es gilt mit dem Satz
des Pythagoras für Skalarprodukträume
.
für alle .
Das Minimum wird dabei eindeutig an dem orthogonal projizierten Vektor
angenommen. Liegt der Vektor
im orthogonalen Komplement des Untervektorraums, dann ist der projizierte Vektor
der Nullvektor.
Allgemeinfall
Ist die Basis
des Unterraums nicht orthogonal, so kann sie mit dem Gram-Schmidtschen
Orthogonalisierungsverfahren orthogonalisiert und so eine Orthogonalbasis
von
erhalten werden. Weiterhin kann ein Vektor auch auf einen affinen Unterraum
mit
orthogonal projiziert werden. Man erhält dann den Allgemeinfall einer
Orthogonalprojektion eines Vektors
auf einen affinen Unterraum
durch
.
Komplementäre Darstellung
Ist nun
eine orthogonale Komplementärbasis
von
,
also eine Orthogonalbasis des Komplements
,
dann erhält man aufgrund von
die komplementäre Darstellung einer Orthogonalprojektion
auf einen affinen Unterraum
als
.
Matrixdarstellung
Koordinaten
Wählt man für den Vektorraum
eine Orthonormalbasis
bezüglich des Skalarprodukts
,
dann kann jeder Vektor
als Koordinatenvektor
über
mit
dargestellt werden. Die Koordinaten
sind dabei genau die Längen der Orthogonalprojektionen des Vektors auf die
Basisvektoren. Das Skalarprodukt
zweier Vektoren
ist in Koordinatendarstellung dann das Standardskalarprodukt
der zugehörigen Koordinatenvektoren
,
wobei
der adjungierte
Vektor (im reellen Fall der transponierte
Vektor) zu
ist.
Darstellung
Sind nun
die Koordinatenvektoren einer Orthogonalbasis
eines Untervektorraums
und
der Koordinatenvektor eines zu projizierenden Vektors
,
dann ist die Koordinatendarstellung einer Orthogonalprojektion
.
Eine Orthogonalprojektion ist in Koordinatendarstellung damit einfach ein Matrix-Vektor-Produkt
mit der Abbildungsmatrix
gegeben durch
.
Sind
die Koordinatenvektoren einer Orthonormalbasis von
,
so hat die Orthogonalprojektionsmatrix
die einfachere Darstellung
.
Jeder Summand ist dabei das dyadische Produkt eines Koordinatenvektors mit sich selbst.
Beispiele
Im Koordinatenraum
ist die Orthogonalprojektionsmatrix auf die Ursprungsgerade mit Richtung
gegeben durch
.
Die Orthogonalprojektionsmatrix auf die Ursprungsebene, die durch
und
aufgespannt wird, ist entsprechend
.
Eigenschaften
Eine Orthogonalprojektionsmatrix ist idempotent, das heißt, es gilt
.
Weiterhin ist sie selbstadjungiert (im reellen Fall symmetrisch), da
ist. Für den Rang und die Spur einer Orthogonalprojektionsmatrix gilt
,
da für idempotente Matrizen Rang und Spur übereinstimmen und die
Einzelmatrizen
jeweils Rang eins besitzen. Die Eigenwerte
einer Orthogonalprojektionsmatrix sind
und
,
wobei die zugehörigen Eigenräume gerade der Untervektorraum
und sein orthogonales Komplement
sind. Die Spektralnorm
einer Orthogonalprojektionsmatrix ist damit, sofern
nicht der Nullvektorraum
ist, gleich eins.
Allgemeinfall
Bilden die Koordinatenvektoren
zwar eine Basis, aber keine Orthogonalbasis des Untervektorraums, so kann man
sie zur Berechnung einer Orthogonalprojektion orthogonalisieren oder ein
entsprechendes lineares Gleichungssystem lösen. Fasst man die Basisvektoren
spaltenweise zu einer Matrix
zusammen, dann hat dieses Gleichungssystem die Gestalt der Normalgleichungen
mit dem Koeffizientenvektor .
Die Matrixdarstellung einer Orthogonalprojektion ist dann aufgrund von
gegeben durch
.
Diese Matrix findet breite Anwendung in der Statistik (siehe Projektionsmatrix
(Statistik)). Eine Orthogonalprojektion auf einen affinen Unterraum
ist in Matrixdarstellung dann die affine
Abbildung
mit der Einheitsmatrix
und mit
als dem Koordinatenvektor von
.
Unter Verwendung homogener
Koordinaten lässt sich jede Orthogonalprojektion auch als ein einfaches
Matrix-Vektorprodukt darstellen.
Komplementäre Darstellung
Eine Orthogonalprojektion auf einen affinen Unterraum
hat die komplementäre Matrixdarstellung
mit der Orthogonalprojektionsmatrix auf den Komplementärraum
gegeben durch
.
Bilden die Koordinatenvektoren
eine Orthogonalbasis des Komplementärraums
,
so hat die komplementäre Orthogonalprojektionsmatrix die Darstellung
.
Funktionalanalysis
In der Funktionalanalysis wird das Konzept der Orthogonalprojektion auf unendlichdimensionale Skalarprodukträume über den reellen oder komplexen Zahlen verallgemeinert und insbesondere auf Funktionenräume angewandt.
Definition
Ist
ein Skalarproduktraum und ist
ein Untervektorraum von
mit orthogonalem
Komplement
,
dann ist eine Orthogonalprojektion ein Operator
(auch orthogonaler Projektor genannt), mit den beiden Eigenschaften
(Projektion)
(Orthogonalität)
wobei
das Bild
und
der Kern
des Operators ist. Der komplementäre Operator
besitzt dann als Bild
und als Kern
.
Existenz und Eindeutigkeit
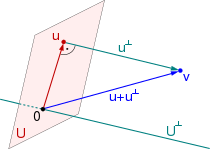
Damit solche Orthogonalprojektionen auch existieren und eindeutig sind,
müssen die betrachteten Räume jedoch eingeschränkt werden. Ist
ein Hilbertraum, also ein vollständiger
Skalarproduktraum, und ist
ein abgeschlossener
Untervektorraum von
,
dann stellt der Projektionssatz
die Existenz und Eindeutigkeit von Orthogonalprojektionen sicher. Zu jedem
Vektor
gibt es dann eindeutige Vektoren
und
,
sodass dieser Vektor die Darstellung
besitzt. Damit bilden
und
eine orthogonale Zerlegung von
,
das heißt, der gesamte Raum
lässt sich als orthogonale
Summe
darstellen.
Ein endlichdimensionaler Untervektorraum ist immer abgeschlossen und auf die
Vollständigkeit von
kann dann auch verzichtet werden.
Darstellung
Jeder Hilbertraum besitzt eine Orthonormalbasis,
die sich allerdings nicht immer explizit angeben lässt. Ist allerdings
ein separabler
Hilbertraum, dann ist eine solche Orthonormalbasis
als Schauderbasis abzählbar,
sodass jeder Vektor
in eine Reihe
entwickelt werden kann.
Eine solche Orthonormalbasis kann stets aus einer linear unabhängigen Teilmenge
von
mit Hilfe des Gram-Schmidtschen Orthogonalisierungsverfahrens erhalten werden.
Ist nun
eine (ebenfalls abzählbare) Orthonormalbasis eines abgeschlossenen
Untervektorraums
,
dann hat eine Orthogonalprojektion die Reihendarstellung
.
Diese Darstellung lässt sich auch auf nicht-separable, also
überabzählbar-dimensionale Hilberträume verallgemeinern. Ist
ein abgeschlossener Untervektorraum eines allgemeinen Hilbertraums und
mit einer beliebigen Indexmenge
eine Orthonormalbasis dieses Untervektorraums, dann hat eine
Orthogonalprojektion die entsprechende Darstellung
,
wobei nur abzählbar viele Summenglieder dieser Summe ungleich null sind.
Diese Reihen sind nach der Besselschen
Ungleichung unbedingt
konvergent und nach der Parsevalschen
Gleichung wird dabei tatsächlich jedes Element von
auf sich selbst abgebildet.
Beispiel
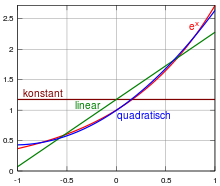
Gegeben sei der Raum
L2 der quadratisch integrierbaren reellen Funktionen im
Intervall
mit dem L2-Skalarprodukt
Für diesen Raum bilden die Legendre-Polynome
ein vollständiges Orthogonalsystem.
Gesucht ist nun die Orthogonalprojektion der Exponentialfunktion
auf den Untervektorraum der linearen
Funktionen. Für diesen Unterraum bilden die beiden Monome
eine Orthogonalbasis, was nach Normierung die Orthonormalbasis
ergibt. Die Orthogonalprojektion von
auf den Untervektorraum der linearen Funktionen ist dann gegeben durch
.
Eigenschaften
Ist
ein Hilbertraum und
ein abgeschlossener Unterraum von
,
dann ist
ein stetiger
linearer Operator mit den folgenden Eigenschaften:
ist eine Projektion, das heißt
.
ist selbstadjungiert, das heißt
mit dem adjungierten Operator
.
ist normal, das heißt
.
ist positiv, das heißt insbesondere
für alle
.
ist eine partielle Isometrie, bei der der isometrische Anteil die Identität ist.
ist genau dann kompakt, wenn
endlichdimensional ist.
ist Bestapproximation in der Skalarproduktnorm, das heißt
.
, falls
, und
, falls
(in der Operatornorm).
Umgekehrt ist eine stetige lineare Projektion ,
die selbstadjungiert oder normal oder positiv oder auf eins normiert ist, eine
Orthogonalprojektion auf den Bildraum
.
Anwendungen
Orthogonalprojektionen besitzen vielfältige Anwendungen, von denen hier nur einige herausgestellt werden:
- Geometrie
- in der analytischen Geometrie bei Abstandsberechnungen und Spiegelungen an Ebenen
- in der Physik bei der Zerlegung von Kräften in ihre Bestandteile
- in der Computergrafik bei der Berechnung von Reflexionen und Schatten
- Lineare Algebra
- bei der Konstruktion von Orthonormalbasen mit dem Gram-Schmidtschen Orthogonalisierungsverfahren
- bei der Lösung linearer Ausgleichsprobleme mit der Methode der kleinsten Quadrate
- bei der iterativen Lösung linearer Gleichungssysteme mit dem Verfahren der konjugierten Gradienten und allgemeinen Krylow-Unterraum-Verfahren
- Funktionalanalysis
- in der Approximationstheorie bei der Bestapproximation von Funktionen
- in der Fourier-Analysis und der Wavelet-Analysis von Signalen
- in der Sobolev-Theorie zur Lösung partieller Differenzialgleichungen
- in der Quantenmechanik zur Beschreibung quantenmechanischer Zustände mittels der Bra-Ket-Notation
- Statistik und Wahrscheinlichkeitstheorie
- bei der Hauptkomponentenanalyse multivariater Datensätze
- bei bedingten Erwartungswerten
Siehe auch
Literatur
- Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 5. Auflage. Springer, 2008, ISBN 3-540-34186-2.
- Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 7. Auflage. Vieweg, 2009, ISBN 3-528-66508-4.
- Dirk Werner: Funktionalanalysis. 5. Auflage. Springer, 2005, ISBN 3-540-21381-3.
Anmerkungen
- ↑ Im Folgenden wird diejenige Variante des komplexen Skalarprodukts verwendet, die linear im ersten und semilinear im zweiten Argument ist.
- ↑
Eine dazu äquivalente Bedingung ist
für alle
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 14.01. 2024