Householdertransformation
In der Mathematik beschreibt die Householdertransformation die Spiegelung eines Vektors an einer Hyperebene durch Null im euklidischen Raum. Im dreidimensionalen Raum ist sie somit eine Spiegelung an einer Ebene (durch den Ursprung). Die Darstellung dieser linearen Abbildung durch eine Matrix wird als Householder-Matrix bezeichnet. Verwendung findet sie vor allem in der numerischen Mathematik, wenn mittels orthogonaler Transformationen Matrizen so gezielt umgeformt werden, dass bestimmte Spaltenvektoren auf das Vielfache des ersten Einheitsvektors abgebildet werden, insbesondere beim QR-Verfahren und der QR-Zerlegung.
Die Householdertransformation wurde 1958 durch den amerikanischen Mathematiker Alston Scott Householder eingeführt.
Definition und Eigenschaften
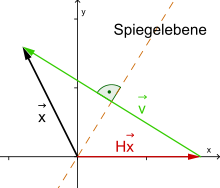
Die Spiegel-Hyperebene kann durch einen Normalenvektor
,
also einen Vektor, der orthogonal
zur Hyperebene ist, definiert werden. Ist
als Spaltenvektor
gegeben und
die Einheitsmatrix,
dann wird die oben beschriebene lineare Abbildung durch die folgende Matrix
dargestellt:
Dabei bezeichnet
die Transponierte
des Spaltenvektors
,
also einen Zeilenvektor. Der Nenner
ist das Skalarprodukt
von
mit sich selbst,
das dyadische
Produkt. Die Matrix
beschreibt die Orthogonalprojektion
auf die durch
gegebene Richtung. Ist
auf die Länge eins normiert, also
,
so vereinfacht sich die Formel zu
Die Spiegelungseigenschaft ersieht man daraus, dass
,
wobei
das Standardskalarprodukt
bezeichnet. Der Term
entspricht dabei dem Abstand des Punktes
zur Hyperebene
.
Der Vektor
wird also in zwei zueinander orthogonale Anteile zerlegt, wobei der erste Anteil
in der Hyperebene liegt und der zweite ein Vielfaches des Vektors
ist. Unter der Spiegelung wird der Anteil in der Ebene invariant gelassen, der
Anteil in Richtung
,
also senkrecht zur Ebene, wird „umgeklappt“, also nun abgezogen statt addiert.
Die Householder-Matrix hat folgende Eigenschaften:
- Sie ist symmetrisch:
- Sie ist orthogonal:
- Sie ist involutorisch:
(Dies folgt aus der Symmetrie und der Orthogonalität.)
- Sie hat den einfachen Eigenwert
−1 zum Eigenvektor
und den
-fachen Eigenwert 1. Der Eigenraum zum Eigenwert 1 ist die Spiegelebene, also das orthogonale Komplement des von
erzeugten eindimensionalen Unterraums.
- Matrix-Vektor-Multiplikationen
mit
sind schnell berechenbar.
Konstruktion einer spezifischen Spiegelung
Es sei ein Vektor a gegeben, der auf ein Vielfaches des Vektors
e gespiegelt werden soll, das heißt, gesucht ist ein Einheitsvektor
v, so dass mit der zugehörigen Householder-Matrix
gilt
.
Geometrisch ist der Vektor v die Richtung einer der zwei
Winkelhalbierenden der Geraden in Richtung a und in Richtung e.
Die Winkelhalbierende ergibt sich, indem man auf beiden Geraden Punkte mit
demselben Abstand zum Nullpunkt wählt und auf der Verbindungsstrecke dieser zwei
Punkte den Mittelpunkt konstruiert. Die Gerade durch Nullpunkt und Mittelpunkt
hat dann die gesuchte Richtung v, der Vektor v selbst ergibt sich
durch Normieren dieser Richtung. Die zweite Winkelhalbierende ergibt sich, indem
die Konstruktion ausgehend von a und -e durchgeführt wird.
Der Einfachheit halber sei e normiert, .
Dann muss, wegen der Orthogonalität der Spiegelung,
gelten. Der gesuchte Spiegelungsvektor v ergibt sich nun durch Normieren
des Differenzvektors
,
also
.
Beide Vorzeichenvarianten führen zum gewünschten Ergebnis (sofern der Nenner
von Null verschieden ist). Aus Gründen numerischer Stabilität wird das Vorzeichen von
so gewählt, dass der Nenner am größten ist, also
gilt.
In der Probe ergibt sich
Beispiel
Am häufigsten wird der Fall betrachtet, in dem
der erste kanonische Basisvektor ist. Sei
in erste Komponente und Restvektor zerlegt. Dann gilt für die Norm
.
Als Vorzeichen von
ist das Vorzeichen von
zu wählen, die Richtung der Spiegelung ist dann
.
Dabei ist
Der Vektor
entsteht durch Normierung dieser Richtung. Nach Umformen stellt sich die Norm
der Richtung als
dar, wobei in dieser Form nur bereits berechnete Zwischenergebnisse benutzt werden. In der unnormierten Variante der Spiegelung ergeben sich weitere Einsparungen an Rechenschritten.
Anwendung: QR-Zerlegung
Householder-Spiegelungen können zur stabilen
Berechnung von QR-Zerlegungen
einer Matrix
verwendet werden, indem zunächst die erste Spalte der Matrix mit einer
Spiegelung
auf das Vielfache des ersten Einheitsvektors gespiegelt wird, wie im letzten
Abschnitt erläutert (jetzt bezeichnet der Index aber die Nummer der Spiegelung).
Danach behandelt man
mit einer Spiegelung
analog, wobei die Spiegelung so konstruiert wird, dass erste Zeile und Spalte
von der Transformation unberührt bleiben. Dies wird erreicht, indem die erste
Komponente des Spiegelungsvektors zu Null gesetzt wird. Zur Bestimmung des
dritten Schrittes geht analog nur die Hauptuntermatrix unter dem dritten
Diagonalelement ein, der Spiegelungsvektor ist Null in den ersten zwei
Komponenten etc. Im
-ten
Schritt wird also die Untermatrix unter der Position
des Produkts
auf die gleiche Art reduziert, bis die Restmatrix
Dreiecksgestalt besitzt. (Im Fall
genügen
Schritte, da die letzte Spalte nicht mehr transformiert werden muss.)
Mit
gilt
,
also ergibt sich die QR-Zerlegung
mit
Man beachte, dass
hier eine quadratische Matrix ist. Meist werden die Matrizen
bzw.
nicht explizit berechnet, sondern man nutzt direkt die Produktform. Dazu werden
die Spiegelvektoren
von
im frei gewordenen Platz der Matrix
gespeichert.
Die Zahl der Operationen für die QR-Zerlegung einer Matrix
mit dem Householder-Verfahren beträgt:
Pseudocode
Da für die meisten Berechnungen das explizite Ausrechnen von
nicht nötig ist, reicht es, nur die Matrix
zu berechnen.
ist die linke Spalte der jeweiligen Untermatrix.
Bei der unten angegebenen Funktion wird das Ergebnis direkt in
geschrieben, so dass nach Abarbeitung des Algorithmus das
in
steht. Die Zeile
könnte also auch weggelassen werden.
function GetR(A)
for k=1…n
z=A(k…m,k)
uk=z
uk(1)+=sign(z(1))*norm(z)
uk=uk/norm(uk)
vk=zeros(m)
vk(k…m)= uk
A=A-(2*vk)*(vk'*A)
R=A
return R
Sollte
dennoch benötigt werden, lässt sich das obere Beispiel einfach erweitern:
function GetR(A)
Q=eye(m)
for k=1…n
z=A(k…m,k)
uk=z
uk(1)+=sign(z(1))*norm(z)
uk=uk/norm(uk)
vk=zeros(m)
vk(k…m)= uk
A=A-(2*vk)*(vk'*A)
Q=Q-Q*vk*(2*vk')
R=A
return R
Siehe auch
Literatur
- Martin Hermann: Numerische Mathematik, 2., überarbeitete und erweiterte Auflage, Oldenbourg Verlag, München, Wien 2006, ISBN 3-486-57935-5, pp. 159–161


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.07. 2020