
Symmetrische Matrix
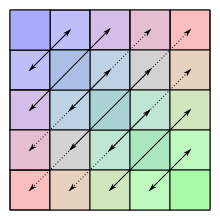
Eine symmetrische Matrix ist in der Mathematik eine quadratische Matrix, deren Einträge spiegelsymmetrisch bezüglich der Hauptdiagonale sind. Eine symmetrische Matrix stimmt demnach mit ihrer transponierten Matrix überein.
Die Summe zweier symmetrischer Matrizen und jedes skalare Vielfache einer symmetrischen Matrix ist wieder symmetrisch. Die Menge der symmetrischen Matrizen fester Größe bildet daher einen Untervektorraum des zugehörigen Matrizenraums. Jede quadratische Matrix lässt sich dabei eindeutig als Summe einer symmetrischen und einer schiefsymmetrischen Matrix schreiben. Das Produkt zweier symmetrischer Matrizen ist genau dann symmetrisch, wenn die beiden Matrizen kommutieren. Das Produkt einer beliebigen Matrix mit ihrer Transponierten ergibt eine symmetrische Matrix.
Symmetrische Matrizen mit reellen Einträgen weisen eine Reihe weiterer besonderer Eigenschaften auf. So ist eine reelle symmetrische Matrix stets selbstadjungiert, sie besitzt nur reelle Eigenwerte und sie ist stets orthogonal diagonalisierbar. Für komplexe symmetrische Matrizen gelten diese Eigenschaften im Allgemeinen nicht; das entsprechende Gegenstück sind dort hermitesche Matrizen. Eine wichtige Klasse reeller symmetrischer Matrizen sind positiv definite Matrizen, bei denen alle Eigenwerte positiv sind.
In der linearen Algebra werden symmetrische Matrizen zur Beschreibung symmetrischer Bilinearformen verwendet. Die Darstellungsmatrix einer selbstadjungierten Abbildung bezüglich einer Orthonormalbasis ist ebenfalls stets symmetrisch. Lineare Gleichungssysteme mit symmetrischer Koeffizientenmatrix lassen sich effizient und numerisch stabil lösen. Weiterhin werden symmetrische Matrizen bei Orthogonalprojektionen und bei der Polarzerlegung von Matrizen verwendet.
Symmetrische Matrizen besitzen Anwendungen unter anderem in der Geometrie, der Analysis, der Graphentheorie und der Stochastik.
Eng verwandt mit den Matrizen sind die Tensoren zweiter Stufe, die ein wichtiges mathematisches Hilfsmittel in den Natur- und Ingenieurswissenschaften, insbesondere in der Kontinuumsmechanik sind, siehe Symmetrische Tensoren.
Definition
Eine quadratische
Matrix
über einem Körper
heißt symmetrisch, wenn für ihre Einträge
für
gilt. Eine symmetrische Matrix ist demnach spiegelsymmetrisch bezüglich ihrer Hauptdiagonale, das
heißt, es gilt
,
wobei
die transponierte
Matrix bezeichnet.
Beispiele
Beispiele für symmetrische Matrizen mit reellen Einträgen sind
.
Allgemein haben symmetrische Matrizen der Größe ,
und
die Struktur
.
Klassen symmetrischer Matrizen beliebiger Größe sind unter anderem
- Diagonalmatrizen, insbesondere Einheitsmatrizen,
- konstante quadratische Matrizen, beispielsweise quadratische Nullmatrizen und Einsmatrizen,
- Hankel-Matrizen, bei denen alle Gegendiagonalen konstante Einträge aufweisen, beispielsweise Hilbert-Matrizen,
- bisymmetrische Matrizen, die sowohl bezüglich der Hauptdiagonale, als auch der Gegendiagonale symmetrisch sind.
Eigenschaften
Einträge

Aufgrund der Symmetrie wird eine symmetrische Matrix
bereits durch ihre
Diagonaleinträge und die
Einträge unterhalb (oder oberhalb) der Diagonalen eindeutig charakterisiert.
Eine symmetrische Matrix weist demnach höchstens
verschiedene Einträge auf. Im Vergleich dazu kann eine nichtsymmetrische
-Matrix
bis zu
unterschiedliche Einträge besitzen, also bei großen Matrizen fast doppelt so
viele. Zur Speicherung symmetrischer Matrizen im Computer gibt es daher
spezielle Speicherformate, die diese Symmetrie ausnutzen.
Summe
Die Summe
zweier symmetrischer Matrizen
ist stets wieder symmetrisch, denn
.
Ebenso ist auch das Produkt
einer symmetrischen Matrix mit einem Skalar
wieder symmetrisch. Nachdem auch die Nullmatrix symmetrisch ist, bildet die
Menge der symmetrischen
-Matrizen
einen Untervektorraum
des Matrizenraums .
Dieser Untervektorraum besitzt die Dimension
,
wobei die Standardmatrizen
,
,
und
,
darin eine Basis
bilden.
Zerlegung
Falls die Charakteristik
des Körpers
ungleich 2 ist, lässt sich jede beliebige quadratische Matrix
eindeutig als Summe
einer symmetrischen Matrix
und einer schiefsymmetrischen
Matrix
schreiben, indem
und
gewählt werden. Die schiefsymmetrischen Matrizen bilden dann ebenfalls einen
Untervektorraum
des Matrizenraums mit Dimension
.
Der gesamte
-dimensionale
Raum
lässt sich folglich als direkte
Summe
der Räume der symmetrischen und der schiefsymmetrischen Matrizen schreiben.
Produkt
Das Produkt
zweier symmetrischer Matrizen
ist im Allgemeinen nicht wieder symmetrisch. Das Produkt symmetrischer
Matrizen ist genau dann symmetrisch, wenn
und
kommutieren,
also wenn
gilt, denn dann ergibt sich
.
Insbesondere sind damit für eine symmetrische Matrix
auch alle ihre Potenzen
mit
und daher auch ihr Matrixexponential
wieder symmetrisch. Für eine beliebige Matrix
sind sowohl die
-Matrix
als auch die
-Matrix
stets symmetrisch.
Kongruenz
Jede Matrix ,
die kongruent
zu einer symmetrischen Matrix
ist, ist ebenfalls symmetrisch, denn es gilt
,
wobei
die zugehörige Transformationsmatrix ist. Matrizen, die ähnlich zu
einer symmetrischen Matrix sind, müssen jedoch nicht notwendigerweise ebenfalls
symmetrisch sein.
Inverse
Ist eine symmetrische Matrix
invertierbar,
dann ist auch ihre Inverse
wieder symmetrisch, denn es gilt
.
Für eine reguläre symmetrische Matrix
sind demnach auch alle Potenzen
mit
wieder symmetrisch.
Reelle symmetrische Matrizen
Symmetrische Matrizen mit reellen Einträgen besitzen eine Reihe weiterer besonderer Eigenschaften.
Normalität
Eine reelle symmetrische Matrix
ist stets normal,
denn es gilt
.
Jede reelle symmetrische Matrix kommutiert also mit ihrer Transponierten. Es gibt allerdings auch normale Matrizen, die nicht symmetrisch sind, beispielsweise schiefsymmetrische Matrizen.
Selbstadjungiertheit
Eine reelle symmetrische Matrix
ist stets selbstadjungiert,
denn es gilt mit dem reellen
Standardskalarprodukt
für alle Vektoren .
Es gilt auch die Umkehrung und jede reelle selbstadjungierte Matrix ist
symmetrisch. Aufgefasst als komplexe
Matrix ist eine reelle symmetrische Matrix stets hermitesch, denn es
gilt
,
wobei
die adjungierte
Matrix zu
und
die konjugierte
Matrix zu
ist. Damit sind reelle symmetrische Matrizen auch selbstadjungiert bezüglich des
komplexen
Standardskalarprodukts.
Eigenwerte
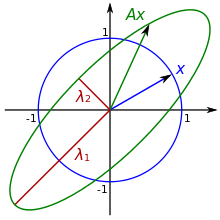
Die Eigenwerte
einer reellen symmetrischen Matrix ,
das heißt die Lösungen der Eigenwertgleichung
,
sind stets reell. Ist nämlich
ein komplexer Eigenwert von
mit zugehörigem Eigenvektor
,
,
dann gilt mit der komplexen Selbstadjungiertheit von
.
Nachdem
für
ist, muss
gelten und der Eigenwert
damit reell sein. Daraus folgt dann auch, dass der zugehörige Eigenvektor
reell gewählt werden kann.
Vielfachheiten
Bei jeder reellen symmetrischen Matrix
stimmen die algebraischen
und die geometrischen
Vielfachheiten aller Eigenwerte überein. Ist nämlich
ein Eigenwert von
mit geometrischer Vielfachheit
,
dann existiert eine Orthonormalbasis
des Eigenraums von
,
welche durch
zu einer Orthonormalbasis des Gesamtraums
ergänzt
werden kann. Mit der orthogonalen
Basistransformationsmatrix
ergibt sich damit die transformierte Matrix
als Blockdiagonalmatrix
mit den Blöcken
und
.
Für die Einträge
von
mit
gilt nämlich mit der Selbstadjungiertheit von
und der Orthonormalität der Basisvektoren
,
wobei >
das Kronecker-Delta
darstellt. Da
nach Voraussetzung keine Eigenvektoren zum Eigenwert
von
sind, kann
kein Eigenwert von
sein. Die Matrix
besitzt daher nach der Determinantenformel
für Blockmatrizen den Eigenwert
genau mit algebraischer Vielfachheit
und aufgrund der Ähnlichkeit
der beiden Matrizen damit auch
.
Diagonalisierbarkeit
Da bei einer reellen symmetrischen Matrix
algebraische und geometrische Vielfachheiten aller Eigenwerte übereinstimmen und
da Eigenvektoren zu verschiedenen Eigenwerten stets linear
unabhängig sind, kann aus Eigenvektoren von
eine Basis
des
gebildet werden. Daher ist eine reelle symmetrische Matrix stets diagonalisierbar, das
heißt, es gibt eine reguläre Matrix
und eine Diagonalmatrix
,
sodass
gilt. Die Matrix
hat dabei die Eigenvektoren
als Spalten und die Matrix
hat die zu diesen Eigenvektoren jeweils zugehörigen Eigenwerte
auf der Diagonalen.
Durch eine Permutation
der Eigenvektoren kann dabei die Reihenfolge der Diagonaleinträge von
beliebig gewählt werden. Daher sind zwei reelle symmetrische Matrizen genau dann
zueinander ähnlich, wenn sie die gleichen Eigenwerte besitzen. Weiterhin sind
zwei reelle symmetrische Matrizen genau dann simultan
diagonalisierbar, wenn sie kommutieren.
Orthogonale Diagonalisierbarkeit
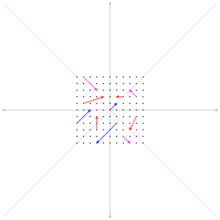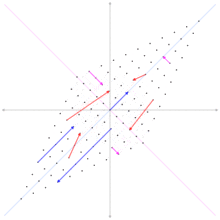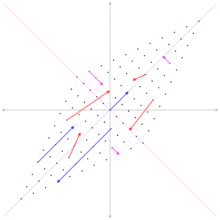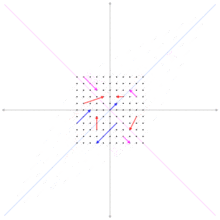
Die Eigenvektoren
zu zwei verschiedenen Eigenwerten
einer reellen symmetrischen Matrix
sind stets orthogonal.
Es gilt nämlich wiederum mit der Selbstadjungiertheit
von
.
Da
und
als verschieden angenommen wurden, folgt daraus dann
.
Daher kann aus Eigenvektoren von
eine Orthonormalbasis des
gebildet werden. Damit ist eine reelle symmetrische Matrix sogar orthogonal
diagonalisierbar, das heißt, es gibt eine orthogonale Matrix
,
mit der
gilt. Diese Darstellung bildet die Grundlage für die Hauptachsentransformation und ist die einfachste Version des Spektralsatzes.
Kenngrößen
Aufgrund der Diagonalisierbarkeit einer reellen symmetrischen Matrix
gilt für ihre Spur
und für ihre Determinante entsprechend
.
Der Rang einer reellen symmetrischen Matrix ist gleich der Anzahl der Eigenwerte ungleich Null, also mit dem Kronecker-Delta
.
Eine reelle symmetrische Matrix ist genau dann invertierbar wenn keiner ihrer Eigenwerte Null ist. Die Spektralnorm einer reellen symmetrischen Matrix ist
und damit gleich dem Spektralradius der Matrix. Die Frobeniusnorm ergibt sich aufgrund der Normalität entsprechend zu
.
Definitheit
Ist
eine reelle symmetrische Matrix, dann wird der Ausdruck
mit
quadratische
Form von
genannt. Je nachdem ob
größer als, größer gleich, kleiner als oder kleiner gleich null für alle
ist, heißt die Matrix
positiv definit, positiv semidefinit, negativ definit oder negativ semidefinit.
Kann
sowohl positive, als auch negative Vorzeichen annehmen, so heißt
indefinit. Die Definitheit einer reellen symmetrischen Matrix kann anhand der Vorzeichen ihrer
Eigenwerte ermittelt werden. Sind alle Eigenwerte positiv, ist die Matrix
positiv definit, sind sie alle negativ, ist die Matrix negativ definit und so
weiter. Das Tripel bestehend aus den Anzahlen
der positiven, negativen und Null-Eigenwerte einer reellen symmetrischen Matrix
wird Signatur
der Matrix genannt. Nach dem Trägheitssatz
von Sylvester bleibt die Signatur einer reellen symmetrischen Matrix unter
Kongruenztransformationen
erhalten.
Abschätzungen
Nach dem Satz
von Courant-Fischer liefert der Rayleigh-Quotient
Abschätzungen für den kleinsten und den größten Eigenwert einer reellen
symmetrischen Matrix
der Form
für alle
mit
.
Gleichheit gilt dabei jeweils genau dann, wenn
ein Eigenvektor zum jeweiligen Eigenwert ist. Der kleinste und der größte
Eigenwert einer reellen symmetrischen Matrix kann demnach durch Minimierung
beziehungsweise Maximierung des Rayleigh-Quotienten ermittelt werden. Eine
weitere Möglichkeit zur Eigenwertabschätzung bieten die Gerschgorin-Kreise,
die für reelle symmetrische Matrizen die Form von Intervallen
haben.
Sind
zwei reelle symmetrische Matrizen mit absteigend sortierten Eigenwerten
und
,
dann gibt die Fan-Ungleichung
die Abschätzung
.
Gleichheit ist hierbei genau dann erfüllt, wenn die Matrizen
und
simultan geordnet diagonalisierbar sind, das heißt, wenn eine orthogonale Matrix
existiert, sodass
und
gelten. Die Fan-Ungleichung stellt eine Verschärfung der Cauchy-Schwarz-Ungleichung
für das Frobenius-Skalarprodukt
und eine Verallgemeinerung der Umordnungs-Ungleichung
für Vektoren dar.
Komplexe symmetrische Matrizen
Zerlegung
Die Zerlegung des komplexen Matrizenraums
als direkte Summe der Räume symmetrischer und schiefsymmetrischer Matrizen
stellt eine orthogonale Summe bezüglich des Frobenius-Skalarprodukts dar. Es gilt nämlich
für alle Matrizen
und
,
woraus
folgt. Die Orthogonalität der Zerlegung gilt entsprechend auch für den reellen
Matrizenraum
.
Spektrum
Bei komplexen Matrizen
hat die Symmetrie keine besonderen Auswirkungen auf das Spektrum.
Eine komplexe symmetrische Matrix kann auch nicht-reelle Eigenwerte besitzen.
Beispielsweise hat die komplexe symmetrische Matrix
die beiden Eigenwerte .
Es gibt auch komplexe symmetrische Matrizen, die nicht diagonalisierbar sind.
Zum Beispiel besitzt die Matrix
den einzigen Eigenwert
mit algebraischer Vielfachheit zwei und geometrischer Vielfachheit eins.
Allgemein ist sogar jede komplexe quadratische Matrix ähnlich zu
einer komplexen symmetrischen Matrix. Daher weist das Spektrum einer komplexen
symmetrischen Matrix keinerlei Besonderheiten auf.
Das komplexe Gegenstück reeller symmetrischer Matrizen sind, was die
mathematischen Eigenschaften betrifft, hermitesche
Matrizen.
Faktorisierung
Jede komplexe symmetrische Matrix
lässt sich durch die Autonne-Takagi-Faktorisierung
in eine unitäre
Matrix ,
eine reelle Diagonalmatrix
und die Transponierte von
zerlegen. Die Einträge der Diagonalmatrix sind dabei die Singulärwerte von
,
also die Quadratwurzeln
der Eigenwerte von
.
Verwendung
Symmetrische Bilinearformen
Ist
ein
-dimensionaler
Vektorraum über dem Körper
,
dann lässt sich jede Bilinearform
nach Wahl einer Basis
für
durch die Darstellungsmatrix
beschreiben. Ist die Bilinearform symmetrisch,
gilt also
für alle
,
dann ist auch die Darstellungsmatrix
symmetrisch. Umgekehrt definiert jede symmetrische Matrix
mittels
eine symmetrische Bilinearform .
Ist eine reelle symmetrische Matrix
zudem positiv definit, dann stellt
ein Skalarprodukt im euklidischen Raum
dar.
Selbstadjungierte Abbildungen
Ist
ein
-dimensionaler
reeller Skalarproduktraum,
dann lässt sich jede lineare
Abbildung
nach Wahl einer Orthonormalbasis
für
durch die Abbildungsmatrix
darstellen, wobei
für
ist. Die Abbildungsmatrix
ist nun genau dann symmetrisch, wenn die Abbildung
selbstadjungiert
ist. Dies folgt aus
,
wobei
und
sind.
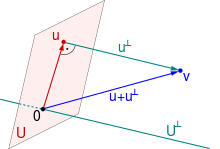
Projektionen und Spiegelungen
Ist wieder
ein
-dimensionaler
reeller Skalarproduktraum und ist
ein
-dimensionaler
Untervektorraum von
,
wobei
die Koordinatenvektoren einer Orthonormalbasis für
sind, dann ist die Orthogonalprojektionsmatrix
auf diesen Untervektorraum
als Summe symmetrischer Rang-Eins-Matrizen ebenfalls symmetrisch. Auch die
Orthogonalprojektionsmatrix auf den Komplementärraum
ist aufgrund der Darstellung
stets symmetrisch. Mit Hilfe der Projektionsmatrizen
und
lässt sich jeder Vektor
in zueinander orthogonale Vektoren
und
zerlegen. Auch die Spiegelungsmatrix
an einem Untervektorraum
ist stets symmetrisch.
Lineare Gleichungssysteme
Das Auffinden der Lösung eines linearen
Gleichungssystems
mit symmetrischer Koeffizientenmatrix
vereinfacht sich, wenn man die Symmetrie der Koeffizientenmatrix ausnutzt. Auf
Grund der Symmetrie lässt sich die Koeffizientenmatrix
als Produkt
mit einer unteren
Dreiecksmatrix
mit lauter Einsen auf der Diagonale und einer Diagonalmatrix
schreiben. Diese Zerlegung wird beispielsweise bei der Cholesky-Zerlegung
positiv definiter symmetrischer Matrizen verwendet, um die Lösung des
Gleichungssystems zu berechnen. Beispiele moderner Verfahren zur numerischen
Lösung großer linearer Gleichungssysteme mit dünnbesetzter
symmetrischer Koeffizientenmatrix sind das CG-Verfahren
und das MINRES-Verfahren.
Polarzerlegung
Jede quadratische Matrix
kann mittels der Polarzerlegung
auch als Produkt
einer orthogonalen Matrix
und einer positiv semidefiniten symmetrischen Matrix
faktorisiert werden. Die Matrix
ergibt sich dabei als die Quadratwurzel
von
.
Ist
regulär, so ist
positiv definit und die Polarzerlegung eindeutig mit
.
Anwendungen
Geometrie

Eine Quadrik im -dimensionalen
euklidischen Raum ist die Nullstellenmenge
eines quadratischen Polynoms
in
Variablen. Jede Quadrik kann somit als Punktmenge der Form
beschrieben werden, wobei
mit
eine symmetrische Matrix,
und
sind.
Analysis
Die Charakterisierung der kritischen
Punkte einer zweimal
stetig differenzierbaren Funktion
kann mit Hilfe der Hesse-Matrix
vorgenommen werden. Nach dem Satz
von Schwarz ist die Hesse-Matrix stets symmetrisch. Je nachdem ob
positiv definit, negativ definit oder indefinit ist, liegt an der kritischen
Stelle
ein lokales
Minimum, ein lokales
Maximum oder ein Sattelpunkt
vor.
Graphentheorie
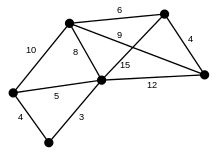
Die Adjazenzmatrix
eines ungerichteten
kantengewichteten
Graphen
mit der Knotenmenge
ist durch
mit
gegeben und damit ebenfalls stets symmetrisch. Auch von der Adjazenzmatrix durch Summation oder Potenzierung abgeleitete Matrizen, wie die Laplace-Matrix die Erreichbarkeitsmatrix oder die Entfernungsmatrix, sind dann symmetrisch. Die Analyse solcher Matrizen ist Gegenstand der spektralen Graphentheorie.
Stochastik
Ist
ein Zufallsvektor bestehend aus
reellen Zufallsvariablen
mit endlicher Varianz,
dann ist die zugehörige Kovarianzmatrix
die Matrix aller paarweisen Kovarianzen
dieser Zufallsvariablen. Nachdem
für
gilt, ist eine Kovarianzmatrix stets symmetrisch.
Symmetrische Tensoren
Tensoren sind ein wichtiges mathematisches Hilfsmittel in den Natur- und Ingenieurswissenschaften, insbesondere in der Kontinuumsmechanik, da sie neben dem Zahlenwert und der Einheit auch noch Informationen über Orientierungen im Raum enthalten. Die Komponenten des Tensors verweisen auf Tupel von Basisvektoren, die durch das dyadische Produkt „⊗“ verknüpft sind. Alles, was oben über reelle symmetrische Matrizen als Ganzem geschrieben steht, lässt sich auf symmetrische Tensoren zweiter Stufe übertragen. Insbesondere haben auch sie reelle Eigenwerte und paarweise orthogonale oder orthogonalisierbare Eigenvektoren. Für symmetrische positiv definite Tensoren zweiter Stufe wird auch ein Funktionswert analog zur Quadratwurzel einer Matrix oder zum Matrixexponential definiert.
Koeffizientenmatrix von symmetrischen Tensoren 2. Stufe
Nicht ohne Weiteres lassen sich die Aussagen über die Einträge in den Matrizen auf Tensoren übertragen, denn bei letzteren hängen sie vom verwendeten Basissystem ab. Nur bezüglich der Standardbasis – oder allgemeiner einer Orthonormalbasis – können Tensoren zweiter Stufe mit einer Matrix identifiziert werden. Der Anschaulichkeit halber beschränkt sich die allgemeine Darstellung hier auf den reellen drei-dimensionalen Vektorraum, nicht zuletzt auch wegen seiner besonderen Relevanz in den Natur- und Ingenieurswissenschaften.
Jeder Tensor zweiter Stufe kann bezüglich zweier Vektorraumbasen
und
als Summe
geschrieben werden. Bei der Transposition werden im dyadischen Produkt die Vektoren vertauscht. Der transponierte Tensor ist somit
Eine mögliche Symmetrie ist hier nicht einfach erkennbar; jedenfalls genügt
die Bedingung
nicht für den Nachweis. Die Bedingung gilt jedoch bezüglich einer
Orthonormalbasis ê1,2,3
Hier kann die Symmetrie
aus seiner Koeffizientenmatrix abgelesen werden:
Dies gilt auch bezüglich einer allgemeinen, nicht orthonormalen, kontravarianten Basis ĝ1,2,3:
Sollen beide Tensoren gleich sein, dann folgt auch hier die Symmetrie der
Koeffizientenmatrix .
In obiger Form wird der Tensor kovariant genannt. Beim kontravarianten Tensor
wird die Duale Basis benutzt, sodass
.
Für ihn folgt die Symmetrie der Koeffizientenmatrix wie beim kovarianten Tensor.
Beim gemischtvarianten Tensor werden beide Basen benutzt
Sind beide Tensoren identisch, ist ,
weswegen die Indizes bei symmetrischen Tensoren übereinander gestellt werden
können:
.
Dann hat man
Die gemischtvariante Koeffizientenmatrix ist beim gemischtvarianten Tensor im
Allgemeinen nicht symmetrisch. Besagtes gilt entsprechend auch für symmetrische
gemischtvariante Tensoren der Form .
Invarianz der Symmetrieeigenschaft
Die Symmetrie eines Tensors ist von Basiswechseln unberührt. Das ist daran ersichtlich, dass die Vektorinvariante, die ausschließlich vom schiefsymmetrischen Anteil bestimmt wird und nur bei symmetrischen Tensoren der Nullvektor ist, invariant gegenüber Basiswechseln ist.
Betrag eines Tensors
Der Betrag eines Tensors, definiert mit der Frobeniusnorm
,
lässt sich bei symmetrischen Tensoren mit den Hauptinvarianten
darstellen:
Symmetrie von Tensoren höherer Stufe
Auch bei Tensoren höherer Stufe werden bei der Transposition die
Basisvektoren in den Dyadischen Produkten vertauscht. Allerdings gibt es dort
mehrere Möglichkeiten die Basisvektoren zu
permutieren und entsprechend gibt es vielfältige Symmetrien bei Tensoren
höherer Stufe. Bei einem Tensor vierter Stufe
wird durch die Notation
der i-te Vektor mit dem k-ten Vektor vertauscht, beispielsweise
Bei der Transposition „⊤“ ohne Angabe der Positionen werden die ersten beiden durch die letzten beiden Vektoren vertauscht:
Symmetrien liegen dann vor, wenn der Tensor mit seiner irgendwie transponierten Form übereinstimmt.
Siehe auch
- Persymmetrische Matrix, eine Matrix die symmetrisch bezüglich ihrer Gegendiagonale ist
- Symmetrischer Operator, eine Verallgemeinerung symmetrischer Matrizen auf unendlichdimensionale Räume
- Symmetrische Orthogonalisierung, ein Orthogonalisierungsverfahren zur Lösung verallgemeinerter Eigenwertprobleme
Literatur
- Hans-Rudolf Schwarz, Norbert Köckler: Numerische Mathematik. 5. überarbeitete Auflage. Teubner, Stuttgart u. a. 2004, ISBN 3-519-42960-8.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.10. 2022