Orthogonale Summe

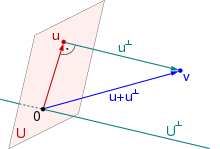
Der dreidimensionale euklidische Raum lässt sich als orthogonale Summe $\scriptstyle V=U\oplus U^{\perp }$ einer Ursprungsebene und einer dazu orthogonalen Ursprungsgeraden darstellen. Jeder Vektor des Raums ist dann die Summe $\scriptstyle v=u+u^{\perp }$ eines Teils in der Ebene und eines Teils auf der Geraden.

Die orthogonale Summe ist im mathematischen Teilgebiet der linearen Algebra eine Konstruktion, die aus einer Familie von Skalarprodukträumen (oder allgemeineren Räumen) einen einzigen Skalarproduktraum, die orthogonale Summe der Familie, bildet, in den sich die Skalarprodukträume als paarweise orthogonale Unterräume einbetten lassen. Die orthogonale Summe ist gewissermaßen die minimal mögliche solcher Konstruktionen. Das auf diesem Raum definierte Skalarprodukt nennt man auch orthogonale Summe oder direkte Summe der einzelnen Skalarprodukte auf den einzelnen Räumen. In der Funktionalanalysis überträgt man diese Konstruktion auf Hilberträume und spricht dann auch von der (direkten) Hilbertsumme oder Hilbertraumsumme.

Äußere orthogonale Summe

Endliche Summen

Zunächst betrachtet man zwei Skalarprodukträume und über demselben Körper mit den Skalarprodukten $\langle \cdot ,\cdot \rangle _{X}$ bzw. $\langle \cdot ,\cdot \rangle _{Y}$ . Die äußere orthogonale Summe

$X\oplus Y$

ist dann die äußere direkte Summe der beiden Vektorräume und , das heißt das kartesische Produkt $X\times Y$ der Mengen und mit komponentenweiser Addition und Skalarmultiplikation. Dieser Raum wird nun mit dem Skalarprodukt

$\langle \,(x_{1},x_{2}),(y_{1},y_{2})\,\rangle _{{X\oplus Y}}=\langle x_{1},y_{1}\rangle _{X}+\langle x_{2},y_{2}\rangle _{Y}$

für $(x_{1},x_{2}),(y_{1},y_{2})\in X\oplus Y$ versehen, der orthogonalen Summe von $\langle \cdot ,\cdot \rangle _{X}$ und $\langle \cdot ,\cdot \rangle _{Y}$ . Mittels der Einbettungen

$x\mapsto (x,0)$ und $y\mapsto (0,y)$

lässt sich mit dem Untervektorraum $X\times \{0\}$ und mit $\{0\}\times Y$ identifizieren, wobei $\{0\}$ der jeweilige Nullvektorraum ist. Ein Vektor $(x,y)\in X\oplus Y$ wird dann einfach als Summe x+y geschrieben, insofern man o.B.d.A. davon ausgehen kann, dass die Räume disjunkt sind. Sind die Vektorräume und über $\mathbb {R}$ oder $\mathbb {C}$ definiert und vollständig, also Hilberträume, dann ist der Raum $X\oplus Y$ bezüglich des Skalarprodukts $\langle \cdot ,\cdot \rangle _{{X\oplus Y}}$ ebenfalls vollständig. Induktiv lassen sich so auch orthogonale Summen für endlich viele Summanden definieren.

Man schreibt die orthogonale Summe auch als $\oplus _{2}$ , etwa wenn auch andere $\ell ^{p}$ -Summen $\oplus _{p}$ auftreten.

Beliebige direkte Summen

Sei $(X_{i})_{i\in I}$ eine Familie von Skalarprodukträumen über demselben Körper mit Skalarprodukten $\langle \cdot ,\cdot \rangle _{{X_{i}}}$ zu einer beliebigen Indexmenge . Die direkte Summe der Vektorräume $X_{i}$ ist der Vektorraum

$\bigoplus _{i}X_{i}=\left\{S\colon I\to \bigcup _{i}X_{i}\mid \forall i:S_{i}\in X_{i},\ \left\{i\in I\mid S(i)\neq 0\right\}{\text{ endlich}}\right\}$

versehen mit der komponentenweisen Addition und Skalarmultiplikation. Auf diesem Raum von Familien von Vektoren definiert man das Skalarprodukt

$\langle \,(x_{i}),(y_{i})\,\rangle _{{\bigoplus _{i}X_{i}}}=\sum _{{i\in I}}\langle x_{i},y_{i}\rangle _{{X_{i}}}$

mit $x_{i},y_{i}\in X_{i}$ , welches wohldefiniert ist, da gemäß Konstruktion der direkten Summe nur endlich viele der Summanden ungleich null sind. Man erhält so die (algebraische) orthogonale direkte Summe. Mittels der Einbettungen

$\mu _{j}\colon X_{j}\to \bigoplus _{i}X_{i},x_{j}\mapsto (x_{i})_{{i\in I}}$ mit $x_{i}={\begin{cases}x_{j}&{\text{für}}\,\,i=j\\0&{\text{sonst}}\end{cases}}$ ,

die Skalarprodukte erhalten, lassen sich die einzelnen Räume wieder mit Untervektorräumen identifizieren und man schreibt einen Vektor $(x_{i})_{i\in I}$ dieses Raums ggf. einfach als Summe $\textstyle \sum _{{i\in I}}x_{i}$ , wobei jedoch nur endlich viele Summanden von null verschieden sein dürfen. Die orthogonale Summe einer leeren Familie ist der Nullvektorraum (versehen mit dem trivialen und einzig möglichen Skalarprodukt). Diese Konstruktion ist völlig analog für beliebige Familien von Moduln über demselben nicht notwendigerweise kommutativen Ring versehen mit beliebigen Sesquilinearformen als Sesquilinearform auf der direkten Summe definiert. Man definiert die direkte Summe auch für Sesquilinearformen, deren erstes und zweites Argument aus verschiedenen Moduln stammen, in diesem Fall kann man jedoch nicht mehr von Orthogonalität der eingebetteten Untermoduln sprechen.

Beliebige Summen von Hilberträumen

Für eine solche unendliche direkte Summe gilt im Allgemeinen nicht mehr, dass die Summe von Hilberträumen wiederum ein Hilbertraum ist, die Vollständigkeit kann also verletzt werden. Daher definiert man für eine Familie $(H_{i})_{{i\in I}}$ von Hilberträumen über demselben Körper ( $\mathbb {R}$ oder $\mathbb {C}$ ) mit Skalarprodukten $\langle \cdot ,\cdot \rangle _{{H_{i}}}$ die orthogonale Summe (bzw. eindeutig gesprochen die Hilbertraumsumme) als die Vervollständigung der obigen (zur Abgrenzung auch algebraisch genannten) orthogonalen direkten Summe. Dies ist gewissermaßen der kleinste Hilbertraum, der die algebraische orthogonale direkte Summe enthält. Man nennt diesen ebenfalls $\bigoplus _{i}H_{i}$ . Konkret lässt sich dieser Raum wie folgt konstruieren:

$\bigoplus _{i}H_{i}=\left\{S\colon I\to \bigcup _{i}H_{i}\mid \forall i:S_{i}\in H_{i},\ \left(\|S_{i}\|_{{H_{i}}}\right)_{i}\in \ell ^{2}(I)\right\}=\left\{S\colon I\to \bigcup _{i}H_{i}\mid \forall i:S(i)\in H_{i},\ \sum _{i}\|S(i)\|_{{H_{i}}}^{2}<\infty \right\}$ ,

wobei die Endlichkeit der Summe so zu lesen ist, dass insbesondere stets nur höchstens abzählbar viele Summanden ungleich null sind. Addition und Skalarmultiplikation sind wiederum komponentenweise erklärt. Das Skalarprodukt definiert man wiederum als

$\langle \,(x_{i}),(y_{i})\,\rangle _{{\bigoplus _{i}H_{i}}}=\sum _{{i\in I}}\langle x_{i},y_{i}\rangle _{{H_{i}}}$ ,

wobei nun die Definition nur noch sicherstellt, dass nur abzählbar viele Summanden ungleich null sind. Die Summe ist also als absolut konvergente Reihe zu lesen. Die Einbettungen $\mu _{i}$ liefern wie zuvor Identifikationen mit Unterhilberträumen und man schreibt einen Vektor $(x_{i})_{i\in I}$ in der orthogonalen Summe ggf. einfach als Summe $\textstyle \sum _{{i\in I}}x_{i}$ , wobei nun nur noch gelten muss, dass die Normen der $x_{i}$ quadratsummabel sind, es können also auch abzählbar unendlich viele von null verschiedene Summanden auftreten.

Die Konstruktion als Vervollständigung zeigt, dass die (algebraische) direkte Summe ein dichter Teilvektorraum der orthogonalen (Hilbertraum-)Summe ist, welche wiederum ein Teilvektorraum des direkten Produktes ist. Im Falle einer unendlichen Familie von Räumen ohne Nullvektorräume sind diese Inklusionen echt.

Falls Verwechslungen mit der (algebraischen) direkten Summe von Vektorräumen möglich sind, schreibt man die orthogonale Summe auch als $\textstyle \overline {\bigoplus _{i}H_{i}}$ . Als Spezialfall einer $\ell ^{p}$ -Summe schreibt man sie als $\textstyle \left(\bigoplus _{i}H_{i}\right)_{2}$ .

Innere orthogonale Summe

Analog zur inneren direkten Summe von Vektorräumen spricht man im Spezialfall der orthogonalen Summe von paarweise orthogonalen Unterhilberträumen eines gegebenen Hilbertraums von einer inneren orthogonalen Summe. Während man bei der inneren orthogonalen Summe die Bedingung der paarweisen Orthogonalität stellt, kann eine äußere orthogonale Summe auch etwa von vielen gleichen Räumen gebildet werden, die dann „kopiert“ werden. Betrachtet man einen Skalarproduktraum, so ist die innere orthogonale Summe von Unterräumen nichts anderes als ihre innere direkte Vektorraumsumme, d.h. ihre lineare Hülle.

Die innere orthogonale (Hilbertraum-)Summe in einem Hilbertraum dagegen ist der Abschluss der linearen Hülle der Summanden. Sie kann leicht durch Orthogonalprojektionen charakterisiert werden: Seien $(H_{i})_{{i\in I}}$ paarweise orthogonale Unterhilberträume eines Hilbertraums , d.h. für $i\neq j$ und $x\in H_{i},y\in H_{j}$ ist $x\perp y$ . Dann existieren die Orthogonalprojektionen $\pi _{i}\colon H\to H_{i}$ auf die Unterhilberträume und deren Summe

$\pi \colon H\to H,x\mapsto \sum _{i}\pi _{i}(x)$ .

ist wiederum eine Orthogonalprojektion. Das Bild von $\pi$ ist gerade die (innere) orthogonale Summe der Räume $H_{i}$ .

Beispiele

Der Raum $\ell^2(I)$ ist gerade der Spezialfall der orthonormalen Summe des eindimensionalen Hilbertraums :

$\ell ^{2}(I)=\bigoplus _{{i\in I}}K$

Für einen Unterhilbertraum $U\subseteq H$ ist gerade die innere orthogonale Summe von und seinem orthogonalen Komplement $U^\perp$ :

$H=U\oplus U^{\perp }$

Der in der Quantenfeldtheorie wichtige antisymmetrische Fockraum ergibt sich als Vervollständigung der äußeren Algebra auf einem Hilbertraum , bzw. als orthogonale Summe der äußeren Potenzen $\Lambda ^{i}(H)$ :

$F_{-}(H)=\bigoplus _{{i\in \mathbb{N} }}\Lambda ^{i}(H)$

Entsprechend ergibt sich der symmetrische Fockraum als Vervollständigung der symmetrischen Algebra, eines anderen Quotienten der Tensoralgebra, bzw. als orthogonale Summe der Räume $S^{i}(H)$ der symmetrischen Tensoren der Stufe über :

$F_{+}(H)=\bigoplus _{{i\in \mathbb{N} }}S^{i}(H)$

Basen und Dimension

Seien $B_{i}\subset H_{i}$ Orthonormalbasen von $H_{i}$ . Dann ist $\textstyle \bigcup _{i}\mu _{i}(B_{i})$ eine Orthonormalbasis von $\textstyle \bigoplus _{i}H_{i}$ . Diese Vereinigung ist disjunkt, da die eingebetteten Unterhilberträume paarweise orthogonal sind und ein Basiselement nie null ist. Somit ist die Hilbertraumdimension der orthogonalen Summe gleich der Summe der Dimensionen der einzelnen Hilberträume:

$\dim \bigoplus _{i}H_{i}=\left|\bigcup _{i}\mu _{i}(B_{i})\right|=\sum _{i}\left|B_{i}\right|=\sum _{i}\dim H_{i}$ .

Insbesondere gilt $\mathbb{R} ^{n}\oplus \mathbb{R} ^{m}\cong \mathbb{R} ^{{n+m}}$ oder allgemeiner $\ell ^{2}(\alpha )\oplus \ell ^{2}(\beta )\cong \ell ^{2}(\alpha +\beta )$ für Kardinalzahlen $\alpha, \beta$ .

Kategorielle Eigenschaften

Im algebraischen Fall der orthogonalen Summe von Skalarprodukträumen bzw. Sesquilinearformen auf Moduln ist die orthogonale Summe der Räume ja nichts anderes als die direkte Summe, die einzelnen Skalarprodukte haben keinerlei Einfluss auf die Struktur dieses Raumes. Diese ist Koprodukt in der entsprechenden Kategorie von Moduln mit linearen Abbildungen. Die endliche direkte Summe ist zusätzlich ein (direktes) Produkt, während sie sich im unendlichen Fall im Allgemeinen von diesem unterscheidet.

Die orthogonale Summe endlich vieler Hilberträume ist analog dazu ein Biprodukt in der Kategorie der Hilberträume mit stetigen linearen Operatoren als Morphismen, d.h. sie ist sowohl (direktes) Produkt als auch Koprodukt (direkte Summe). Zudem ist dieses Biprodukt in dem Sinne kompatibel mit der $\dagger$ -Struktur, die durch die Adjungierung gegeben ist, dass

$\mu _{i}^{\dagger }=\pi _{i}$ und

$\pi _{i}^{\dagger }=\mu _{i}$ .

Da zudem für die Nullmorphismen (d.h. konkret die Nullfunktionen) $(0\colon X\to Y)^{\dagger }=(0\colon Y\to X)$ für beliebige Hilberträume X,Y gilt, spricht man von einer Biprodukt- $\dagger$ -Kategorie.

Dagegen ist die orthogonale Summe einer unendlichen Familie von Nicht-Nullräumen in dieser Kategorie weder Produkt noch Koprodukt: Um einzusehen, dass es sich um kein Produkt handelt, betrachte für Einheitsvektoren $v_{i}\in H_{i}$ die Morphismen $f_{i}\colon K\to H_{i},\lambda \mapsto \lambda v_{i}$ . Wäre $\textstyle \bigoplus _{i}H_{i}$ mit den Projektionen $\pi_i$ ein Produkt, so müsste es eine stetige lineare Abbildung $\textstyle f\colon K\to \bigoplus _{i}H_{i}$ geben mit $f_{i}=\pi _{i}f$ , d.h. f(1) hätte in jeder Komponente den Betrag , womit keine Quadratsummabilität mehr vorläge. Dual dazu betrachte für die Verletzung der Koprodukteigenschaft betrachte o.B.d.A. $I=\mathbb{N} \setminus \{0\}$ (für überabzählbares wähle überzählige $g_{i}$ als null) und die Morphismen $g_{i}\colon H_{i}\to K,u\mapsto i\cdot \langle u,v\rangle _{{H_{i}}}$ . Nun müsste ein Morphismus $\textstyle g\colon \bigoplus _{i}H_{i}\to K$ existieren mit $g_{i}=g\mu _{i}$ . Ein solches könnte jedoch allenfalls unbeschränkt und lediglich dicht definiert sein, denn für

$u=\sum _{i}{\frac {1}{i}}v_{i}\in \bigoplus _{i}H_{i}$

müsste

$g(u)=\sum _{i}i\cdot \langle {\frac {1}{i}}v_{i},v_{i}\rangle =\sum _{i}1$

sein, was jedoch divergiert. Tatsächlich existieren in dieser Kategorie weder beliebige (kleine) Produkte, noch Koprodukte. Die Beispiele zeigen auch, dass viele denkbare Einschränkungen der Morphismen keine Abhilfe verschaffen – die Beispielmorphismen sind von Rang eins und damit sehr gutartig. Die Wahl linearer Kontraktionen (die im Falle der Banachräume zur Vollständigkeit der Kategorie führt und im Falle der Hilberträume unitäre Operatoren als die Isomorphismen fixiert) ist auch nicht möglich, in diesem Fall wäre die orthogonale Summe nicht einmal mehr endliches Produkt oder Koprodukt. Ein Ausweichen auf dicht definierte Operatoren ist nicht möglich, da diese nicht unter Komposition abgeschlossen sind und damit keine Kategorie bilden.

Siehe auch

Die orthogonale Summe ist der Spezialfall der ℓ^p-Summe von Banachräumen für .
Ebenso ist die orthogonale Summe Spezialfall des direkten Integrals von Hilberträumen mit dem Zählmaß.
Das Hilbertraum-Tensorprodukt ist eine weitere wichtige Konstruktion auf Hilberträumen.

Basierend auf einem Artikel in:

Wikipedia.de