Gerschgorin-Kreis

Gerschgorin-Kreise dienen in der numerischen linearen Algebra, einem Teilgebiet der Mathematik, zur Abschätzung von Eigenwerten. Mit ihrer Hilfe können einfach Gebiete angegeben werden, in welchen sich die Eigenwerte einer Matrix befinden und unter besonderen Bedingungen sogar wie viele Eigenwerte in diesen enthalten sind.

Sie sind benannt nach dem weißrussischen Mathematiker Semjon Aronowitsch Gerschgorin.

Definition

Sei eine quadratische Matrix mit Einträgen aus $\mathbb {C}$ (also $A\in {\mathbb {C}}^{{n\times n}}$ ), dann ist der zum i-ten Diagonalelement $a_{{ii}}$ gehörende Gerschgorin-Kreis folgendermaßen definiert:

${\bar S}_{i}:={\bar S}\left(a_{{ii}},\sum _{{j=1,j\neq i}}^{n}\left|a_{{ij}}\right|\right)$ für $i=1,\ldots,n$

wobei ${\bar S}(x,r)$ mit $x\in {\mathbb {C}},r\in {\mathbb {R^{{+}}}}$ die abgeschlossene Kreisscheibe mit Radius um den Punkt bezeichnet.

Da die Menge der Eigenwerte (das Spektrum) von identisch mit der von $A^{T}$ ist, kann eine weitere Familie von Kreisen mit denselben Eigenschaften auch spaltenweise bestimmt werden:

${\bar S}_{j}:={\bar S}\left(a_{{jj}},\sum _{{i=1,i\neq j}}^{n}\left|a_{{ij}}\right|\right)$ für $j=1,\ldots,n$

Abschätzung von Eigenwerten

Es gilt:

Das Spektrum von ist eine Teilmenge von $\bigcup _{{i=1}}^{{n}}{\bar S}_{i}$
Falls es eine Teilmenge von $\{1,\ldots ,n\}$ gibt, sodass:

$\bigcup _{{i\in I}}{\bar S}_{i}\cap \bigcup _{{i\notin I}}{\bar S}_{i}=\emptyset$

dann beinhaltet $\bigcup _{{i\in I}}{\bar S}_{i}$ genau $\left|I\right|$ Eigenwerte (samt Vielfachheiten) der Matrix .

Oder einprägsamer: Jede Zusammenhangskomponente der Vereinigung aller Gerschgorin-Kreisscheiben enthält genauso viele Eigenwerte wie Diagonalelemente der Matrix .

Durch die Möglichkeit, die Kreise sowohl zeilen- als auch spaltenweise zu berechnen (die Eigenwerte der transponierten Matrix sind dieselben), können bei nichtsymmetrischen Matrizen zwei Abschätzungen pro Diagonalelement gefunden werden.

Beispiele

Gerschgorin-Kreise zu Matrix A

Zu der Matrix

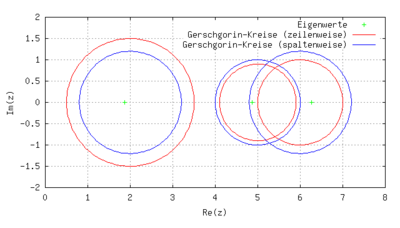
$A={\begin{pmatrix}2&1&0.5\\0.2&5&0.7\\1&0&6\end{pmatrix}}$

gibt es folgende Gerschgorin-Kreise (spalten- und zeilenweise):

${\bar S}(2,1.2)$ und ${\bar S}(2,1.5)$ zum Diagonalelement $a_{11}$
${\bar S}(5,1)$ und ${\bar S}(5,0.9)$ zum Diagonalelement $a_{{22}}$
${\bar S}(6,1.2)$ und ${\bar S}(6,1)$ zum Diagonalelement $a_{{33}}$

Da der Mengendurchschnitt ${\bar S}(2,1.2)\cap {\bigl (}{\bar S}(5,1)\cup {\bar S}(6,1.2){\bigr )}=\emptyset$ leer ist, befindet sich in ${\bar S}(2,1.2)$ genau ein Eigenwert und in ${\bar S}(5,0.9)\cup {\bar S}(6,1)$ befinden sich genau zwei.

Die tatsächlichen Eigenwerte der Matrix sind gerundet 1,8692, 4,8730 und 6,2578 und tatsächlich in den oben angegebenen Gebieten enthalten.

Die Matrix

$B={\begin{pmatrix}8&0&1\\0&7&0\\1&0&5\\\end{pmatrix}}$

ist symmetrisch und reell, somit sind alle Eigenwerte reell und es gibt folgende reelle Intervalle (Gerschgorin Kreise):

$\lbrack 7,9\rbrack ={\bar S}(8,1)$ zum Diagonalelement $b_{{11}}$
$\lbrack 7,7\rbrack ={\bar S}(7,0)$ zum Diagonalelement $b_{{22}}$
$\lbrack 4,6\rbrack ={\bar S}(5,1)$ zum Diagonalelement $b_{{33}}$

Da in der zweiten Spalte und Zeile dieser Matrix nur das Diagonalelement $b_{{22}}$ verschieden von Null ist, kann ein Eigenwert mit $b_{{22}}=7$ leicht bestimmt werden, die beiden anderen liegen in den Intervallen $\lbrack 7,9\rbrack$ und $\lbrack 4,6\rbrack$ , somit kann direkt als positiv definit identifiziert werden. Die tatsächlichen Eigenwerte der Matrix sind $\{7,\,{\tfrac {13\pm {\sqrt {13}}}2}\}$ , also ungefähr 4,6972, 7 und 8,3028.

Verwendung

Die Gerschgorin-Kreise bieten in der Numerik eine einfache Möglichkeit, Eigenschaften von Matrizen zu bestimmen. Enthält z.B. kein Gerschgorin-Kreis den Nullpunkt, so ist die Matrix invertierbar. Diese Eigenschaft wird im Begriff der strikt diagonaldominanten Matrix zusammengefasst. Genauso lässt sich bei symmetrischen bzw. hermiteschen Matrizen die Definitheit oftmals mithilfe der Gerschgorin-Kreise grob abschätzen.

Siehe auch

Satz von Gerschgorin: Anwendung auf Polynomnullstellen
Satz von Courant-Fischer: alternative Charakterisierung der Eigenwerte symmetrischer oder hermitescher Matrizen

Basierend auf einem Artikel in:

Wikipedia.de