Numerische lineare Algebra

Die Modellierung durch finite Elemente, wie hier zur Spannungsanalyse eines Hubkolbens (Dieselmotor), führt auf lineare Gleichungssysteme mit sehr vielen Gleichungen und Unbekannten.

Die numerische lineare Algebra ist ein zentrales Teilgebiet der numerischen Mathematik. Sie beschäftigt sich mit der Entwicklung und der Analyse von Rechenverfahren (Algorithmen) für Problemstellungen der linearen Algebra, insbesondere der Lösung von linearen Gleichungssystemen und Eigenwertproblemen. Solche Probleme spielen in allen Natur- und Ingenieurwissenschaften, aber auch in der Ökonometrie und in der Statistik eine große Rolle.

Die Algorithmen der numerischen linearen Algebra lassen sich grob in zwei Gruppen einteilen: in die direkten Verfahren, die theoretisch nach endlich vielen Rechenschritten die exakte Lösung eines Problems liefern, und in die iterativen Verfahren, bei denen die exakte Lösung schrittweise immer genauer angenähert wird. Da aber auch die direkten Verfahren wegen der beim Rechnen mit endlicher Genauigkeit entstehenden Rundungsfehler nur Näherungen für die exakte Lösung liefern, ist diese Unterscheidung nur für die Entwicklung und Untersuchung der Verfahren selbst von Bedeutung; für den praktischen Einsatz spielt sie keine große Rolle. Historisch gehen die ersten systematischen Verfahren aus beiden Gruppen – das direkte gaußsche Eliminationsverfahren und das iterative Gauß-Seidel-Verfahren – auf Carl Friedrich Gauß zurück. Beispiele für bedeutende Verfahren des 20. Jahrhunderts, die zahlreiche Verbesserungen und Weiterentwicklungen zur Folge hatten, sind das Zerlegungsverfahren von André-Louis Cholesky, das QR-Verfahren für Eigenwertprobleme von John G. F. Francis und Wera Nikolajewna Kublanowskaja sowie das CG-Verfahren von Eduard Stiefel und Magnus Hestenes als erster Vertreter der wichtigen Krylow-Unterraum-Verfahren.

Einführung in die Problemstellungen

Ein – auch historisch gesehen – zentraler Anfangspunkt der elementaren linearen Algebra sind lineare Gleichungssysteme. Wir betrachten Gleichungen der Gestalt

für Unbekannte . Die Koeffizienten und sind gegebene Zahlen; die gesuchten Werte für sollen so bestimmt werden, dass alle Gleichungen erfüllt werden. Die Koeffizienten lassen sich zu einer Matrix zusammenfassen; die Zahlen und die Unbekannten bilden Spaltenvektoren und . Auf diese Weise ergibt sich die Matrix-Vektor-Darstellung

eines linearen Gleichungssystems: Gesucht ist ein Vektor , der bei der Matrix-Vektor-Multiplikation mit der gegebenen Matrix den gegebenen Vektor ergibt. Als Teilgebiet der Numerik betrachtet auch die numerische lineare Algebra nur sogenannte korrekt gestellte Probleme, also insbesondere nur solche Probleme, die eine Lösung besitzen und bei denen die Lösung eindeutig bestimmt ist. Insbesondere wird im Folgenden stets angenommen, dass die Matrix regulär ist, also eine Inverse besitzt. Dann gibt es für jede rechte Seite eine eindeutig bestimmte Lösung des linearen Gleichungssystems, die formal als angegeben werden kann.

Viele wichtige Anwendungen führen allerdings auf lineare Gleichungssysteme mit mehr Gleichungen als Unbekannten. In der Matrix-Vektor-Darstellung hat in diesem Fall die Matrix mehr Zeilen als Spalten. Solche überbestimmten Systeme haben im Allgemeinen keine Lösung. Man behilft sich deshalb damit, den Vektor so zu wählen, dass die Differenz , das Residuum, in einem noch festzulegenden Sinn „möglichst klein“ wird. Beim mit Abstand wichtigsten Fall, dem sogenannten linearen Ausgleichsproblem, wird dazu die Methode der kleinsten Quadrate verwendet: Hierbei wird so gewählt, dass die Quadratsumme minimal wird, wobei die Komponenten des Differenzvektors bezeichnen. Mithilfe der euklidischen Norm lässt sich das auch so schreiben: Man wähle so, dass minimal wird.

Neben den linearen Gleichungen sind die Eigenwertprobleme ein weiteres zentrales Thema der linearen Algebra. Gegeben ist hierbei eine Matrix mit Zeilen und Spalten; gesucht sind Zahlen und Vektoren , sodass die Gleichung

erfüllt ist. Man nennt dann einen Eigenvektor von zum Eigenwert . Das Problem, alle Eigenwerte und Eigenvektoren einer Matrix zu bestimmen, ist gleichbedeutend damit sie zu diagonalisieren. Das bedeutet: Man finde eine reguläre Matrix und eine Diagonalmatrix mit . Die Diagonaleinträge von sind dann die Eigenwerte von und die Spalten von die zugehörigen Eigenvektoren.

Diese Probleme treten in allen Natur- und Ingenieurwissenschaften auf. Sie spielen aber auch in den Wirtschaftswissenschaften sowie in der Statistik – und damit in allen Gebieten, die sich statistischer Methoden bedienen – eine große Rolle. Lineare Gleichungssysteme beschreiben beispielsweise Modelle in der Statik, elektrische Netzwerke oder volkswirtschaftliche Verflechtungen. So scheinbar unterschiedliche Aufgabenstellungen wie die Stabilitätsuntersuchung dynamischer Systeme, Resonanzphänomene bei Schwingungen, die Bestimmung eines PageRanks oder die Hauptkomponentenanalyse in der Statistik führen alle auf Eigenwertprobleme. Lineare Gleichungen entstehen auch durch Linearisierung und Diskretisierung innerhalb anderer numerischer Verfahren. So lassen sich beispielsweise zahlreiche Modelle in Naturwissenschaft und Technik durch partielle Differentialgleichungen beschreiben. Ihre numerische Lösung durch Differenzen- oder Finite-Elemente-Verfahren führt auf Systeme mit sehr vielen Unbekannten.

In diesem Übersichtsartikel wird der Einfachheit halber angenommen, dass alle gegebenen Matrizen und Vektoren reell sind, das heißt, dass alle ihre Einträge reelle Zahlen sind. Meist lassen sich die angesprochenen Verfahren direkt auf komplexe Zahlen verallgemeinern; an die Stelle der orthogonalen Matrizen tritt dann beispielsweise ihr komplexes Pendant, die unitären Matrizen. Mitunter ist es auch vorteilhaft, ein gegebenes komplexes Problem – etwa durch Betrachtung von Real- und Imaginärteil – auf ein reelles zurückzuführen. Zusatzüberlegungen treten allerdings bei Eigenwertproblemen mit nichtsymmetrischen reellen Matrizen auf, denn diese können auch nichtreelle Eigenwerte und Eigenvektoren haben.

Geschichte

Die Anfänge: Gauß und Jacobi

Lithographie von Gauß in den Astronomischen Nachrichten, 1828 von Bendixen

Bereits seit der Antike sind Lösungen konkreter Problemstellungen überliefert, die aus heutiger Sicht als lineare Gleichungssysteme angesehen werden können. Die Neun Kapitel der Rechenkunst, in denen der Stand der chinesischen Mathematik des 1. Jahrhunderts n. Chr. zusammengefasst ist, enthielten dabei bereits tabellarische Rechenvorschriften, die Eliminationsverfahren in Matrixdarstellung entsprachen. Die systematische Untersuchung linearer Gleichungssysteme setzte gegen Ende des 17. Jahrhunderts mit ihrer Formulierung mithilfe allgemeiner Koeffizienten ein. Nach Vorarbeiten von Gottfried Wilhelm Leibniz und Colin Maclaurin veröffentlichte Gabriel Cramer 1750 eine explizite Lösungsformel für beliebig viele Unbekannte mithilfe von Determinanten. Mit dieser cramerschen Regel war das Problem theoretisch vollständig gelöst, auch in Hinblick auf Existenz und Eindeutigkeit von Lösungen. Für deren praktische Berechnung erwies sich die Formel jedoch als völlig ungeeignet, weil der Rechenaufwand dabei mit der Anzahl der Unbekannten astronomisch schnell anwächst (siehe auch Cramersche Regel#Rechenaufwand).

Die erste Verwendung und Beschreibung systematischer Rechenverfahren für lineare Gleichungen geht auf Carl Friedrich Gauß (1777–1855) zurück. Zu Beginn des 19. Jahrhunderts waren die Bestimmung der Bahndaten astronomischer Objekte und die Landesvermessung durch Triangulation die wichtigsten Anwendungsaufgaben der mathematischen Praxis. 1801 erregte Gauß großes Aufsehen, als es ihm gelang, die Bahn des neu entdeckten Kleinplaneten Ceres aus wenigen Beobachtungen so genau zu bestimmen, dass Ceres Ende des Jahres wiedergefunden werden konnte. Für das zugehörige überbestimmte Gleichungssystem verwendete er die von ihm entdeckte Methode der kleinsten Quadrate. Das von ihm zur Berechnung der Lösung eingesetzte Eliminationsverfahren beschrieb Gauß systematisch ab 1809 im Rahmen der Bahnbestimmung des Asteroiden Pallas, allerdings noch direkt angewendet auf Quadratsummen.

Carl Jacobi

Auch das erste Iterationsverfahren zur Lösung linearer Gleichungssysteme – das Gauß-Seidel-Verfahren – stammt von Gauß. In einem Brief an Christian Ludwig Gerling berichtete er 1823 von einem neuen einfachen Verfahren, mit dem die Lösung Schritt für Schritt immer besser angenähert werden könne. Gauß, der inzwischen mit der Triangulation des Königreichs Hannover beschäftigt war, schreibt darin, er rechne fast jeden Abend noch einen Iterationsschritt; das sei eine angenehme Abwechslung zur einförmigen Aufnahme der Messdaten. Das Verfahren sei so wenig anfällig für Fehler, dass es sich sogar „halb im Schlaf“ ausführen lasse. 1845 veröffentlichte Carl Gustav Jacob Jacobi ein anderes, ähnliches Iterationsverfahren, das Jacobi-Verfahren. Als Philipp Ludwig von Seidel, ein Schüler Jacobis, 1874 ein System mit 72 Unbekannten lösen musste, entwickelte er eine modifizierte, verbesserte Version dieser Methode. Wie sich im Nachhinein herausstellte, ist dieses Verfahren äquivalent zum Iterationsverfahren von Gauß, von dem Seidel jedoch vermutlich nichts wusste. Jacobi veröffentlichte 1846 auch ein iteratives Verfahren zur Transformation von Matrizen, das sich zur Lösung des Eigenwertproblems für symmetrische Matrizen eignet und heute ebenfalls als Jacobi-Verfahren bezeichnet wird. Er selbst verwendete es jedoch nur als Vorbereitungsschritt, um die Diagonaleinträge der Matrix stärker dominant zu machen.

20. Jahrhundert

Im Jahr 1923 wurde ein von André-Louis Cholesky entwickeltes Verfahren veröffentlicht, das bestimmte lineare Gleichungssysteme löst, indem die Koeffizientenmatrix in ein Produkt zweier einfacherer Matrizen zerlegt wird, die Cholesky-Zerlegung. Auch das gaußsche Eliminationsverfahren stellte sich im Nachhinein als ein Spezialfall solcher Matrixzerlegungsverfahren heraus. Algorithmen aus dieser Verfahrensgruppe sind auch heute noch die Standardverfahren zur Lösung mäßig großer Systeme.

Ab Ende der 1920er Jahre kamen auch neue Ideen zur iterativen Lösung von Eigenwertproblemen auf, beginnend 1929 mit der Vorstellung der Potenzmethode durch Richard von Mises. Wie auch bei der Weiterentwicklung zur inversen Iteration durch Helmut Wielandt 1944, können mit diesen einfachen Vektoriterationsverfahren immer nur Eigenvektoren zu einem einzelnen Eigenwert berechnet werden. Eine vollständige Lösung des Eigenwertproblems für beliebige Matrizen blieb aufwändig. Der Durchbruch kam hier 1961–1962 mit der Entwicklung des QR-Verfahrens durch den britischen Informatiker John G. F. Francis und unabhängig davon durch die russische Mathematikerin Wera Nikolajewna Kublanowskaja. Während Kublanowskaja in ihrer Arbeit von Anfang an ein tiefes Verständnis der Konvergenzeigenschaften der Methode aufzeigte, arbeitete Francis vor allem an Implementierungsdetails, die das Verfahren schnell und stabil machten. Das QR-Verfahren ist bis heute das Standardverfahren zur Berechnung aller Eigenwerte und Eigenvektoren nicht allzu großer Matrizen.

Eduard Stiefel, 1955

Die Lösung linearer Gleichungssysteme mit sehr großen Matrizen, wie sie bei der Diskretisierung von partiellen Differentialgleichungen auftreten, blieb weiterhin schwierig. Diese Matrizen haben nur relativ wenige Einträge, die ungleich null sind, und es ist von entscheidender Bedeutung, dass ein numerisches Verfahren diese Eigenschaft ausnutzt. Ein neuer Ansatz dazu, der sich als Startpunkt zahlreicher Weiterentwicklungen herausstellen sollte, war das 1952 von Eduard Stiefel und Magnus Hestenes entwickelte CG-Verfahren. Dabei wird das lineare Gleichungssystem in dem Spezialfall, dass die Matrix symmetrisch und zusätzlich positiv definit ist, durch ein äquivalentes Optimierungsproblem ersetzt. Als noch fruchtbarer erwies sich ein anderer Zugang zum CG-Verfahren, der gleichzeitig von Cornelius Lanczos entdeckt wurde: Die durch das CG-Verfahren berechneten Näherungen befinden sich in einer aufsteigenden Kette von Unterräumen, den Krylow-Räumen.

Trotz der Entdeckung dieser Zusammenhänge dauerte es relativ lange, bis konkrete Verallgemeinerungen des CG-Verfahrens entwickelt wurden. Das 1974 von Roger Fletcher veröffentlichte BiCG-Verfahren ist zwar theoretisch für beliebige Matrizen anwendbar, erwies sich jedoch in der Praxis in vielen Fällen als instabil. Das 1975 erschienene MINRES-Verfahren ist ein Krylow-Unterraum-Verfahren, für das die Matrix zwar symmetrisch sein muss, aber nicht unbedingt positiv definit wie beim CG-Verfahren. In der Folgezeit wurden zahlreiche Weiterentwicklungen untersucht, insbesondere Stabilisierungsversuche für das BiCG-Verfahren. Ein Beispiel für ein weit verbreitetes Krylow-Unterraum-Verfahren für beliebige lineare Gleichungssysteme ist eine Verallgemeinerung des MINRES-Verfahrens, das 1986 von Yousef Saad und Martin H. Schultz vorgestellte GMRES-Verfahren. Weitere Verfahren verwenden Synthesen aus Ideen der BiCG-Gruppe und GMRES, so das QMR-Verfahren (Roland W. Freund und Noel M. Nachtigal, 1991) sowie das TFQMR-Verfahren (Freund, 1993). Von Anfang an wurden Krylow-Unterraum-Verfahren auch zur Berechnung von Eigenwerten verwendet, Ausgangspunkte waren hier ein Verfahren von Lanczos 1950 und das Arnoldi-Verfahren von Walter Edwin Arnoldi 1951.

Grundprinzipien

Ausnutzung von Strukturen

Besetzungsstruktur einer dünnbesetzten Matrix, wie sie bei der Finite-Elemente-Methode auftritt; die kleinen schwarzen Quadrate stehen für die Matrixeinträge ungleich null.

Modelle und Fragestellungen in Wissenschaft und Technik können auf Probleme der linearen Algebra mit Millionen von Gleichungen führen. Die Einträge einer Matrix mit einer Million Zeilen und Spalten benötigen im double-precision-Format 8 Terabyte Speicherplatz. Das zeigt, dass bereits die Bereitstellung der Daten eines Problems, geschweige denn seine Lösung, eine Herausforderung darstellen, wenn nicht auch seine spezielle Struktur berücksichtigt wird. Glücklicherweise führen viele wichtige Anwendungen – wie beispielsweise die Diskretisierung partieller Differentialgleichungen mit der Finite-Elemente-Methode – zwar auf sehr viele Gleichungen, in jeder einzelnen Gleichung kommen jedoch nur relativ wenige Unbekannte vor. Für die zugehörige Matrix bedeutet das, dass es in jeder Zeile nur wenige Einträge ungleich null gibt, die Matrix ist, wie man sagt, dünnbesetzt. Es gibt zahlreiche Methoden, um solche Matrizen effizient abzuspeichern und ihre Struktur auszunutzen. Verfahren, in denen Matrizen nur in Matrix-Vektor-Produkten vorkommen, sind für dünnbesetzte Probleme besonders gut geeignet, da dabei alle Multiplikationen und Additionen mit null nicht explizit ausgeführt werden müssen. Algorithmen, bei denen die Matrix selbst umgeformt wird, sind hingegen meist nur schwierig zu implementieren, da dann die Dünnbesetztheit im Allgemeinen verloren geht.

Allgemein hat die Besetzungsstruktur, also die Anzahl und die Position der Matrixeinträge ungleich null, einen sehr großen Einfluss auf die theoretischen und numerischen Eigenschaften eines Problems. Das wird am Extremfall von Diagonalmatrizen, also Matrizen, die nur auf der Hauptdiagonale Einträge ungleich null haben, besonders deutlich. Ein lineares Gleichungssystem mit einer Diagonalmatrix kann einfach gelöst werden, indem die Einträge auf der rechten Seite durch die Diagonalelemente dividiert werden, also mittels Divisionen. Auch lineare Ausgleichsprobleme und Eigenwertprobleme sind für Diagonalmatrizen trivial. Die Eigenwerte einer Diagonalmatrix sind ihre Diagonalelemente und die zugehörigen Eigenvektoren die Standardbasisvektoren .

Ein weiterer wichtiger Spezialfall sind die Dreiecksmatrizen, bei denen alle Einträge oberhalb oder unterhalb der Hauptdiagonale null sind. Gleichungssysteme mit solchen Matrizen können durch Vorwärts- bzw. Rückwärtseinsetzen einfach von oben nach unten bzw. von unten nach oben der Reihe nach aufgelöst werden. Die Eigenwerte von Dreiecksmatrizen sind wiederum trivialerweise die Einträge auf der Hauptdiagonale; zugehörige Eigenvektoren können ebenfalls durch Vorwärts- oder Rückwärtseinsetzen bestimmt werden. Ein weiterer häufiger Spezialfall dünnbesetzter Matrizen sind die Bandmatrizen: Hier sind nur die Hauptdiagonale und einige benachbarte Nebendiagonalen mit Einträgen ungleich null besetzt. Eine Abschwächung der oberen Dreiecksmatrizen sind die oberen Hessenbergmatrizen, bei den auch die Nebendiagonale unter der Hauptdiagonale besetzt ist. Eigenwertprobleme lassen sich mit relativ geringem Aufwand in äquivalente Probleme für Hessenberg- oder Tridiagonalmatrizen transformieren.

Aber nicht nur die Besetzungsstruktur, sondern auch andere Matrixeigenschaften spielen für die Entwicklung und Analyse numerischer Verfahren eine wichtige Rolle. Viele Anwendungen führen auf Probleme mit symmetrischen Matrizen. Insbesondere die Eigenwertprobleme sind deutlich einfacher zu handhaben, wenn die gegebene Matrix symmetrisch ist, aber auch bei linearen Gleichungssystemen reduziert sich in diesem Fall der Lösungsaufwand im Allgemeinen um etwa die Hälfte. Weitere Beispiele für Typen von Matrizen, für die spezialisierte Algorithmen existieren, sind die Vandermonde-Matrizen, die Toeplitz-Matrizen und die zirkulanten Matrizen.

Fehleranalyse: Vektor- und Matrixnormen

Als Maße für die „Größe“ eines Vektors werden in der Mathematik unterschiedliche Vektornormen verwendet. Am bekanntesten und verbreitetsten ist die euklidische Norm

,

also die Wurzel aus der Summe der Quadrate aller Vektorkomponenten. Bei der bekannten geometrischen Veranschaulichung von Vektoren als Pfeile im zwei- oder dreidimensionalen Raum entspricht dies gerade der Pfeillänge. Je nach untersuchter Fragestellung können jedoch auch andere Vektornormen wie etwa die Maximumsnorm oder die 1-Norm geeigneter sein.

Sind Vektoren, wobei als eine Näherung für aufgefasst werden soll, so lässt sich mithilfe einer Vektornorm die Genauigkeit dieser Näherung quantifizieren. Die Norm des Differenzvektors

wird als (normweiser) absoluter Fehler bezeichnet. Betrachtet man den absoluten Fehler im Verhältnis zur Norm des „exakten“ Vektors erhält man den (normweisen) relativen Fehler

.

Da der relative Fehler nicht durch die Skalierung von und beeinflusst wird, ist dieser das Standardmaß für den Unterschied der beiden Vektoren und wird oft auch vereinfacht nur als „Fehler“ bezeichnet.

Auch die „Größe“ von Matrizen wird mit Normen gemessen, den Matrixnormen. Für die Wahl einer Matrixnorm ist es wesentlich, dass sie zur verwendeten Vektornorm „passt“, insbesondere soll die Ungleichung für alle erfüllt sein. Definiert man für eine gegebene Vektornorm als die kleinste Zahl , sodass für alle gilt, dann erhält man die sogenannte natürliche Matrixnorm. Für jede Vektornorm gibt es also eine davon induzierte natürliche Matrixnorm: Für die euklidische Norm ist das die Spektralnorm , für die Maximumsnorm ist es die Zeilensummennorm und für die 1-Norm die Spaltensummennorm . Analog zu Vektoren kann mithilfe einer Matrixnorm der relative Fehler

bei einer Näherung einer Matrix durch eine Matrix quantifiziert werden.

Kondition und Stabilität

Zweidimensionale Veranschaulichung: Die Multiplikation mit einer Matrix A verzerrt den Einheitskreis (blau) zu einer Ellipse (grün). Die Konditionszahl von A ist das Verhältnis von großer Halbachse λ₁ zu kleiner Halbachse λ₂, sie misst also die Stärke der Verzerrung.

Bei Problemen aus der Praxis sind gegebene Größen meist mit Fehlern behaftet, den Datenfehlern. Zum Beispiel kann bei einem linearen Gleichungssystem die gegebene rechte Seite aus einer Messung stammen und daher eine Messabweichung aufweisen. Aber auch bei theoretisch beliebig genau bekannten Größen lassen sich Rundungsfehler bei ihrer Darstellung im Computer als Gleitkommazahlen nicht vermeiden. Es muss also davon ausgegangen werden, dass anstelle des exakten Systems in Wirklichkeit ein System mit einer gestörten rechten Seite und dementsprechend einer „falschen“ Lösung vorliegt. Die grundlegende Frage ist nun, wie stark sich Störungen der gegebenen Größen auf Störungen der gesuchten Größen auswirken. Wenn der relative Fehler der Lösung nicht wesentlich größer ist als die relativen Fehler der Eingangsgrößen, spricht man von einem gut konditionierten, anderenfalls von einem schlecht konditionierten Problem. Für das Beispiel linearer Gleichungssysteme lässt sich hierzu die Abschätzung

beweisen. Das Problem ist also gut konditioniert, wenn , das Produkt der Norm der Koeffizientenmatrix und der Norm ihrer Inversen, klein ist. Diese wichtige Kenngröße heißt Konditionszahl der Matrix und wird mit bezeichnet. In realen Problemen wird meist nicht nur, wie hier dargestellt, die rechte Seite fehlerbehaftet sein, sondern auch die Matrix . Dann gilt eine ähnliche, kompliziertere Abschätzung, in der aber ebenfalls die wesentliche Kennzahl zur Bestimmung der Kondition des Problems bei kleinen Datenfehlern ist. 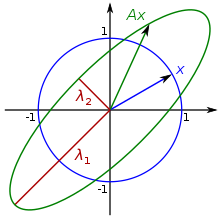Die Definition der Konditionszahl lässt sich auf nicht quadratische Matrizen verallgemeinern und spielt dann auch eine wesentliche Rolle bei der Analyse linearer Ausgleichsprobleme. Wie gut ein solches Problem konditioniert ist, hängt allerdings nicht nur wie bei linearen Gleichungssystemen von der Konditionszahl der Koeffizientenmatrix ab, sondern auch von der rechten Seite , genauer vom Winkel zwischen den Vektoren und . Nach dem Satz von Bauer-Fike lässt sich auch die Kondition des Eigenwertproblems mit Konditionszahlen beschreiben. Hier ist es jedoch nicht die Zahl , mit der sich Störungen der Eigenwerte abschätzen lassen, sondern , die Konditionszahl der Matrix , die via diagonalisiert.

Während die Kondition eine Eigenschaft des zu lösenden Problems ist, ist Stabilität eine Eigenschaft des dafür verwendeten Verfahrens. Ein numerischer Algorithmus liefert – auch bei exakt gedachten Eingangsdaten – im Allgemeinen nicht die exakte Lösung des Problems. Zum Beispiel muss ein iteratives Verfahren, das eine wahre Lösung schrittweise immer genauer annähert, nach endlich vielen Schritten mit der bis dahin erreichten Näherungslösung abbrechen. Aber auch bei direkten Verfahren, die theoretisch in endlich vielen Rechenschritten die exakte Lösung ergeben, kommt es bei der Umsetzung auf dem Computer bei jeder Rechenoperation zu Rundungsfehlern. In der numerischen Mathematik werden zwei unterschiedliche Stabilitätsbegriffe verwendet, die Vorwärtsstabilität und Rückwärtsstabilität. Sei dazu allgemein eine Eingabegröße eines Problems und seine exakte Lösung, aufgefasst als Wert einer Funktion angewendet auf . Auch wenn man die Eingabegröße als exakt vorgegeben betrachtet, wird die Berechnung mit einem Algorithmus ein anderes, „falsches“ Ergebnis liefern, aufgefasst als Wert einer anderen, „falschen“ Funktion ebenfalls angewendet auf . Ein Algorithmus heißt vorwärtsstabil, wenn sich nicht wesentlich stärker von unterscheidet, als es aufgrund der Fehler in der Eingangsgröße und der Kondition des Problems sowieso zu erwarten wäre. Mit einer formalen Definition dieses Begriffs erhält man zwar ein naheliegendes und relativ anschauliches Maß für die Stabilität, aber bei komplizierten Algorithmen ist es oft schwierig, ihre Vorwärtsstabilität zu untersuchen. Daher wird im Allgemeinen nach einer Idee von James H. Wilkinson zunächst eine sogenannte Rückwärtsanalyse betrachtet: Dazu wird ein bestimmt mit , das heißt: Der durch das Verfahren berechnete „falsche“ Wert wird aufgefasst als „richtiger“ Wert, der aber mit einem anderen Wert der Eingabegröße berechnet wurde. Ein Algorithmus heißt rückwärtsstabil, wenn sich nicht wesentlich stärker von unterscheidet, als es aufgrund der Fehler in dieser Eingangsgröße sowieso zu erwarten wäre. Es lässt sich beweisen, dass ein rückwärtsstabiler Algorithmus auch vorwärtsstabil ist.

Orthogonalität und orthogonale Matrizen

Wie die lineare Algebra zeigt, besteht ein enger Zusammenhang zwischen Matrizen und Basen des Vektorraums . Sind linear unabhängige Vektoren im gegeben, so sind diese eine Basis des Raums und jeder andere Vektor kann eindeutig als Linearkombination der Basisvektoren dargestellt werden. Ein Basiswechsel entspricht dabei der Multiplikation gegebener Vektoren und Matrizen mit einer Transformationsmatrix. Einen wichtigen Spezialfall bilden die Orthonormalbasen. Hierbei sind die Basisvektoren paarweise orthogonal zueinander („stehen senkrecht aufeinander“) und sind zudem alle auf euklidische Länge 1 normiert, so wie die Standardbasis im dreidimensionalen Raum. Fasst man die Basisvektoren spaltenweise zu einer Matrix

zusammen, so erhält man im Fall einer Orthonormalbasis eine sogenannte orthogonale Matrix.

Orthonormalbasen und orthogonale Matrizen besitzen zahlreiche bemerkenswerte Eigenschaften, auf denen die wichtigsten Verfahren der modernen numerischen linearen Algebra basieren. Die Tatsache, dass bei einer orthogonalen Matrix die Spalten eine Orthonormalbasis bilden, lässt sich in Matrixschreibweise durch die Gleichung ausdrücken, wobei die transponierte Matrix und die Einheitsmatrix bezeichnen. Das zeigt wiederum, dass eine orthogonale Matrix regulär ist und ihre Inverse gleich ihrer Transponierten ist: . Die Lösung eines linearen Gleichungssystems lässt sich daher sehr einfach bestimmen, es gilt . Eine andere grundlegende Eigenschaft ist es, dass eine Multiplikation eines Vektors mit einer orthogonalen Matrix seine euklidische Norm unverändert lässt

.

Damit folgt für die Spektralnorm und für die Konditionszahl ebenfalls

,

denn ist ebenfalls eine orthogonale Matrix. Multiplikationen mit orthogonalen Matrizen bewirken also keine Vergrößerung des relativen Fehlers.

Orthogonale Matrizen spielen auch eine wichtige Rolle in der Theorie und der numerischen Behandlung von Eigenwertproblemen. Nach der einfachsten Version des Spektralsatzes lassen sich symmetrische Matrizen orthogonal diagonalisieren. Damit ist gemeint: Zu einer Matrix , für die gilt, existiert eine orthogonale Matrix und eine Diagonalmatrix mit

.

Auf der Diagonale von stehen die Eigenwerte von und die Spalten von bilden eine Orthonormalbasis aus Eigenvektoren. Insbesondere ist nach dem oben erwähnten Satz von Bauer-Fike das Eigenwertproblem für symmetrische Matrizen stets gut konditioniert. Mit der sogenannten schurschen Normalform existiert eine Verallgemeinerung dieser orthogonalen Transformation für nichtsymmetrische Matrizen.

Eine Multiplikation mit einer Householder-Matrix spiegelt einen gegebenen Vektor bei geeigneter Wahl der Spiegelebene auf die x-Achse.

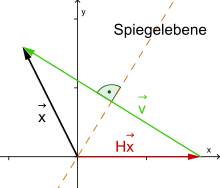
Es gibt zwei spezielle, leicht handhabbare Arten orthogonaler Matrizen, die in zahllosen konkreten Verfahren der numerischen linearen Algebra zum Einsatz kommen: die Householder-Matrizen und die Givens-Rotationen. Householder-Matrizen haben die Gestalt

mit einem Vektor mit . Geometrisch beschreiben sie Spiegelungen des -dimensionalen Raums an der -dimensionalen Hyperebene durch den Nullpunkt, die orthogonal zu ist. Ihre wesentliche Eigenschaft ist die folgende: Zu einem gegebenen Vektor lässt sich leicht ein Vektor bestimmen, sodass die zugehörige Householder-Matrix den Vektor auf ein Vielfaches von transformiert: mit . Dieses transformiert also alle Einträge von bis auf den ersten zu null. Wendet man auf diese Weise geeignete Householder-Transformationen Spalte für Spalte nacheinander auf eine Matrix an, so können alle Einträge von unterhalb der Hauptdiagonale zu null transformiert werden.

Givens-Rotationen sind spezielle Drehungen des , die eine zweidimensionale Ebene drehen und die anderen Dimensionen fest lassen. Die Transformation eines Vektors mit einer Givens-Rotation verändert daher nur zwei Einträge von . Durch geeignete Wahl des Drehwinkels kann dabei einer der beiden Einträge auf null gesetzt wird. Während Householder-Transformationen, angewendet auf Matrizen, ganze Teilspalten transformieren, können Givens-Rotationen dazu verwendet werden, gezielt einzelne Matrixeinträge zu ändern.

Householder-Transformationen und Givens-Rotationen können also dazu benutzt werden, eine gegebene Matrix auf eine obere Dreiecksmatrix zu transformieren, oder anders ausgedrückt, eine QR-Zerlegung in eine orthogonale Matrix und eine obere Dreiecksmatrix zu berechnen. Die QR-Zerlegung ist ein wichtiges und vielseitiges Werkzeug, das in zahlreichen Verfahren aus allen Bereichen der numerischen linearen Algebra zum Einsatz kommt.

Ähnlichkeitstransformationen

In der linearen Algebra wird zur Untersuchung des Eigenwertproblems einer Matrix mit Zeilen und Spalten das charakteristische Polynom verwendet, ein Polynom vom Grad . Die Eigenwerte von sind genau die Nullstellen von . Mit dem Fundamentalsatz der Algebra ergibt sich daraus direkt, dass genau Eigenwerte besitzt, wenn sie mit ihrer Vielfachheit gezählt werden. Allerdings können diese Eigenwerte, auch bei reellen Matrizen, komplexe Zahlen sein. Ist jedoch eine reelle symmetrische Matrix, dann sind ihre Eigenwerte alle reell.

Das charakteristische Polynom hat zwar eine große theoretische Bedeutung für das Eigenwertproblem, zur numerischen Berechnung ist es jedoch nicht geeignet. Das liegt vor allem daran, dass das Problem, aus gegebenen Koeffizienten die Nullstellen des zugehörigen Polynoms zu berechnen, im Allgemeinen sehr schlecht konditioniert ist: Kleine Störungen wie Rundungsfehler an Koeffizienten eines Polynoms können zu einer starken Verschiebung seiner Nullstellen führen. Damit würde ein gegebenenfalls gut konditioniertes Problem – die Berechnung der Eigenwerte – durch ein zwar mathematisch äquivalentes, aber schlecht konditioniertes Problem – die Berechnung der Nullstellen des charakteristischen Polynoms – ersetzt. Viele numerische Verfahren zur Berechnung von Eigenwerten und Eigenvektoren beruhen daher auf einer anderen Grundidee, den Ähnlichkeitstransformationen: Zwei quadratische Matrizen und werden ähnlich genannt, wenn es eine reguläre Matrix mit

gibt. Es kann gezeigt werden, dass zueinander ähnliche Matrizen die gleichen Eigenwerte haben, bei einer Ähnlichkeitstransformation der Matrix auf die Matrix ändern sich also die gesuchten Eigenwerte nicht. Auch die zugehörigen Eigenvektoren lassen sich leicht ineinander umrechnen: Ist ein Eigenvektor von , dann ist ein Eigenvektor von zum gleichen Eigenwert. Das führt zu Grundideen, die in zahlreichen Algorithmen zum Einsatz kommen. Die Matrix wird durch Ähnlichkeitstransformation in eine Matrix überführt, für die das Eigenwertproblem effizienter zu lösen ist, oder es wird eine Folge von Ähnlichkeitstransformationen konstruiert, bei denen sich die Matrix einer Diagonal- oder Dreiecksmatrix immer weiter annähert. Aus den oben genannten Gründen werden dabei für die Transformationsmatrizen meist orthogonale Matrizen verwendet.

Verfahren und Verfahrensklassen

Gaußsches Eliminationsverfahren

Das klassische Eliminationsverfahren von Gauß zur Lösung linearer Gleichungssysteme ist ein Ausgangspunkt und Vergleichsmaßstab für weiterentwickelte Verfahren. Es wird aber auch immer noch als einfaches und zuverlässiges Verfahren – insbesondere in seiner Modifikation als LR-Zerlegung (siehe unten) – für nicht zu große, gut konditionierte Systeme in der Praxis verbreitet eingesetzt. Das Verfahren eliminiert systematisch Variablen aus den gegebenen Gleichungen, indem geeignete Vielfache einer Gleichung von einer anderen Gleichung subtrahiert werden, bis ein System in Stufenform entsteht, das der Reihe nach von unten nach oben aufgelöst werden kann.

Numerische Überlegungen kommen ins Spiel, wenn die Stabilität des Verfahrens betrachtet wird. Soll mit dem -ten Diagonalelement der Matrix ein Element in derselben Spalte eliminiert werden, dann muss mit dem Quotienten

das -fache der -ten Zeile von der -Zeile subtrahiert werden. Dazu muss zumindest gelten, was sich durch geeignete Zeilenvertauschungen für eine reguläre Matrix stets erreichen lässt. Aber mehr noch: Ist sehr klein im Vergleich zu , dann ergäbe sich ein sehr großer Betrag von . In den nachfolgenden Schritten bestünde dann die Gefahr von Stellenauslöschungen durch Subtraktionen großer Zahlen und das Verfahren wäre instabil. Daher ist es wichtig, durch Zeilenvertauschungen, sogenannte Pivotisierung, dafür zu sorgen, dass die Beträge möglichst klein bleiben.

Faktorisierungsverfahren

Die wichtigsten direkten Verfahren zur Lösung linearer Gleichungssysteme lassen sich als Faktorisierungsverfahren darstellen. Deren Grundidee ist es, die Koeffizientenmatrix des Systems in ein Produkt aus zwei oder mehr Matrizen zu zerlegen, allgemein etwa . Das lineare Gleichungssystem lautet damit und wird in zwei Schritten gelöst: Zuerst wird die Lösung des Systems berechnet und anschließend die Lösung des Systems . Es gilt dann , also ist die Lösung des ursprünglichen Problems. Auf den ersten Blick scheint dabei nur die Aufgabe, ein lineares Gleichungssystem zu lösen, durch die Aufgabe, zwei lineare Gleichungssysteme zu lösen, ersetzt zu werden. Die Idee dahinter ist es jedoch, die Faktoren und so zu wählen, dass die beiden Teilsysteme wesentlich einfacher zu lösen sind als das Ausgangssystem. Ein offensichtlicher Vorteil der Verfahrensklasse ergibt sich im Fall, dass mehrere lineare Gleichungssysteme mit derselben Koeffizientenmatrix , aber unterschiedlichen rechten Seiten gelöst werden sollen: Die Faktorisierung von , im Allgemeinen der aufwändigste Verfahrensschritt, muss dann nur einmal berechnet werden.

LR-Zerlegung

Das gaußsche Eliminationsverfahren kann als Faktorisierungsverfahren aufgefasst werden. Trägt man die Koeffizienten für in eine Matrix ein, ergibt sich ohne Zeilenvertauschungen mit einer unteren Dreiecksmatrix und einer oberen Dreiecksmatrix . Zusätzlich ist unipotent, das heißt alle Einträge auf der Hauptdiagonale von sind gleich 1. Wie gesehen müssen im Allgemeinen bei der Gauß-Elimination Zeilen von vertauscht werden. Das lässt sich formal mit Hilfe einer Permutationsmatrix darstellen, indem anstelle von die zeilenpermutierte Matrix faktorisiert wird:

.

Nach dem Grundprinzip der Faktorisierungsverfahren werden zur Lösung von also zunächst wie beschrieben die Dreiecksmatrizen und sowie gegebenenfalls die zugehörige Permutation bestimmt. In nächsten Schritt wird mit der zeilenpermutierten rechten Seite durch Vorwärtseinsetzen und schließlich durch Rückwärtseinsetzen gelöst.

Die LR-Zerlegung und damit das gaußsche Eliminationsverfahren ist mit geeigneter Pivotisierung „fast immer stabil“, das heißt in den meisten praktischen Anwendungsaufgaben tritt keine große Fehlerverstärkung auf. Es lassen sich jedoch pathologische Beispiele angeben, bei denen die Verfahrensfehler exponentiell mit der Anzahl der Unbekannten anwachsen.

Cholesky-Zerlegung

Die Cholesky-Zerlegung ist wie die LR-Zerlegung eine Faktorisierung der Matrix in zwei Dreiecksmatrizen für den in vielen Anwendungen auftretenden Fall, dass symmetrisch und positiv definit ist, also erfüllt und nur positive Eigenwerte besitzt. Unter diesen Voraussetzungen gibt es eine untere Dreiecksmatrix mit

.

Ein allgemeiner Ansatz für die Matrixeinträge von führt auf ein explizites Verfahren, mit dem diese spaltenweise oder zeilenweise nacheinander berechnet werden können, das Cholesky-Verfahren. Durch diese Ausnutzung der Symmetrie von reduziert sich der Rechenaufwand gegenüber der LR-Zerlegung auf etwa die Hälfte.

Symmetrische und positiv definite Koeffizientenmatrizen treten klassisch bei der Formulierung der sogenannten Normalgleichungen zur Lösung linearer Ausgleichsprobleme auf. Man kann zeigen, dass das Problem, zu minimieren, äquivalent damit ist, das lineare Gleichungssystem

zu lösen. Die Koeffizientenmatrix dieser Normalgleichungen ist symmetrisch und, wenn die Spalten von linear unabhängig sind, auch positiv definit. Es kann also mit dem Cholesky-Verfahren gelöst werden. Dieses Vorgehen empfiehlt sich jedoch nur für gut konditionierte Probleme mit wenigen Unbekannten. Im Allgemeinen ist nämlich das System der Normalgleichungen deutlich schlechter konditioniert als das ursprünglich gegebene lineare Ausgleichsproblem. Es ist dann besser, nicht den Umweg über die Normalgleichungen zu gehen, sondern direkt eine QR-Zerlegung von zu verwenden.

QR-Zerlegung

Das lineare Gleichungssystem kann nach der Berechnung einer QR-Zerlegung

direkt nach dem allgemeinen Prinzip der Faktorisierungsverfahren gelöst werden; es ist nur noch mit durch Rückwärtseinsetzen zu bestimmen. Aufgrund der guten Kondition orthogonaler Matrizen treten dabei die möglichen Instabilitäten der LR-Zerlegung nicht ein. Allerdings ist der Rechenaufwand im Allgemeinen etwa doppelt so groß, sodass unter Umständen eine Abwägung der Verfahren getroffen werden muss.

Die QR-Zerlegung ist auch das gängige Verfahren zur Lösung nicht zu großer, gut konditionierter linearer Ausgleichsprobleme. Für das Problem

Minimiere

gilt mit und

.

Dabei wurde verwendet, dass orthogonal ist, also die euklidische Norm erhält, und dass gilt. Der letzte Ausdruck lässt sich einfach durch Rückwärtseinsetzen der ersten Zeilen von minimieren.

Fixpunktiteration mit Splitting-Verfahren

Eine völlig andere Idee, um zu lösen, besteht darin, einen Startvektor zu wählen und daraus schrittweise , immer neue Näherungen an die gesuchte Lösung zu berechnen. Im Fall der Konvergenz der Folge gegen wird dann diese Iteration nach einer geeigneten Anzahl von Schritten mit einer ausreichend genauen Näherung für abgebrochen. Die einfachsten und wichtigsten Verfahren dieser Art verwenden eine Iteration der Gestalt

mit einer geeigneten Matrix und einem geeigneten Vektor . Es lässt sich beweisen, dass solche Verfahren genau dann konvergieren, wenn alle Eigenwerte von einen Betrag echt kleiner als 1 haben. In diesem Fall konvergieren die Iterierten gegen eine Lösung der Gleichung , also gegen einen Fixpunkt der Iterationsfunktion .

Ein systematisches Vorgehen bei der Suche nach geeigneten Algorithmen dieser Gestalt ermöglicht die Idee der Splitting-Verfahren. Dabei wird die Matrix in eine Summe

zerlegt mit einer leicht zu invertierenden Matrix und dem Rest . Durch Einsetzen und Umstellen ergibt sich damit aus die Fixpunktgleichung

.

Mit und erhält man so ein Iterationsverfahren der Gestalt , das im Falle der Konvergenz die Lösung von liefert. Die Konvergenzgeschwindigkeit ist umso größer, je kleiner der betragsgrößte Eigenwert der Iterationsmatrix ist. Dieser lässt sich auch durch beliebige Matrixnormen von abschätzen.

Als klassische Beispiele für Splitting-Verfahren verwendet das Jacobi-Verfahren für die Diagonalmatrix mit der Hauptdiagonale von , das Gauß-Seidel-Verfahren den unteren Dreiecksanteil von . Zur Konvergenzbeschleunigung der Fixpunktverfahren lässt sich die Idee der Relaxation nutzen. Denkt man sich die Iteration in der Form

mit der Korrektur im -ten Schritt dargestellt, geht man mit einem geeignet gewählten Relaxationsparameter zu

über. Zum Beispiel erhält man auf diese Weise aus dem Gauß-Seidel-Verfahren das SOR-Verfahren.

Jacobi-Verfahren zur Eigenwertberechnung

Ein einfaches, aber zuverlässiges iteratives Verfahren zur Lösung des Eigenwertproblems für symmetrische Matrizen ist das Jacobi-Verfahren. Es erzeugt durch sukzessive Ähnlichkeitstransformationen mit Givens-Rotationen eine Folge von symmetrischen Matrizen, die alle ähnlich zu der gegebenen symmetrischen Matrix sind und gegen eine Diagonalmatrix konvergieren. Bricht man das Verfahren nach einer geeigneten Anzahl von Schritten ab, erhält man deshalb mit den Diagonaleinträgen von Näherungen für die gesuchten Eigenwerte von .

In jedem Schritt wird die Givens-Rotation, in diesem Zusammenhang auch als Jacobi-Rotation bezeichnet, so gewählt, dass der Eintrag an der Matrixposition und der symmetrisch dazu liegende bei zu null transformiert werden. Dabei ist jedoch zu beachten, dass bei dieser Transformation die ganze -te und -te Zeile sowie die ganze -te und -te Spalte der Matrix geändert wird. Deshalb werden die in einem Schritt erzeugten Nullen im Allgemeinen in den folgenden Schritten wieder zunichtegemacht. Dennoch konvergieren bei geeigneter Wahl der Positionen für die Jacobi-Rotationen alle Nichtdiagonalelemente gegen null. Das klassische Jacobi-Verfahren wählt dazu in jedem Iterationsschritt diejenige Position , an der sich das Nichtdiagonalelement mit dem größten Absolutbetrag befindet. Bei einer Handrechnung war diese Position normalerweise schnell zu erkennen, bei der Umsetzung als Computerprogramm ist der Aufwand für die Suche danach im Vergleich zu den übrigen Rechenoperationen jedoch erheblich. Daher wird heute meist das zyklische Jacobi-Verfahren verwendet. Dabei werden die Positionen in einer vorher fest gewählten Reihenfolge zyklisch durchlaufen, etwa einfach spaltenweise. Es lässt sich beweisen, dass sowohl das klassische als auch das zyklische Jacobi-Verfahren stets konvergieren. Im Vergleich zu moderneren Algorithmen ist die Konvergenz allerdings relativ langsam. Für dünnbesetzte Matrizen ist das Jacobi-Verfahren nicht geeignet, da im Laufe der Iteration die Matrix mit immer mehr Nichtnulleinträgen aufgefüllt wird.

Vektoriteration

Eine einfache Ausgangsidee zur Berechnung von Eigenvektoren einer Matrix ist die Potenzmethode. Ein Startvektor wird iterativ immer wieder mit multipliziert

oder, ausgedrückt mit der -ten Matrixpotenz, es wird berechnet. Dahinter steckt die geometrische Anschauung, dass der Vektor durch in jedem Schritt am stärksten in die Richtung des Eigenvektors mit dem größten Eigenwert gestreckt wird. In dieser einfachen Form ist die Vektoriteration jedoch für die Praxis ungeeignet, da im Allgemeinen die Einträge von schnell sehr klein oder sehr groß werden. Daher wird der Vektor in jedem Schritt zusätzlich zur Multiplikation mit noch mit einer Vektornorm auf normiert. Man kann dann unter gewissen Voraussetzungen an die Lage der Eigenwerte beweisen, dass dieses Verfahren bis auf möglicherweise einen skalaren Vorfaktor tatsächlich gegen einen Eigenvektor zum betragsgrößten Eigenwert konvergiert.

Wendet man diese Idee formal auf die inverse Matrix an, so erhält man einen Eigenvektor zum betragskleinsten Eigenwert von . Hierzu wird freilich nicht die Inverse selbst berechnet, sondern es wird in jedem Schritt das lineare Gleichungssystem

gelöst. Eine weitere Verallgemeinerung der Idee erhält man mithilfe eines sogenannten Shiftparameters . Ein Eigenvektor von zu dem am nächsten bei liegenden Eigenwert ist nämlich auch ein Eigenvektor zum betragskleinsten Eigenwert der „geshifteten“ Matrix . Mit der zugehörigen Iteration

und Normierung von in jedem Schritt ergibt sich das Verfahren der inversen Vektoriteration.

Vektoriterationsverfahren berechnen also zunächst einen bestimmten Eigenvektor von , der zugehörige Eigenwert kann mithilfe des Rayleigh-Quotienten erhalten werden. Sie sind offenbar dann gut geeignet, wenn – wie häufig in bestimmten Anwendungsfällen – nur der größte, nur der kleinste oder allgemeiner nur ein einzelner Eigenwert mitsamt seinem Eigenvektor gesucht ist.

QR-Verfahren

Das QR-Verfahren ist zurzeit der wichtigste Algorithmus zu Berechnung aller Eigenwerte und Eigenvektoren von nicht zu großen vollbesetzten Matrizen . Es ist ein Iterationsverfahren, das in jedem Schritt eine QR-Zerlegung verwendet, um durch wiederholte Ähnlichkeitstransformationen eine Matrixfolge zu erzeugen, die schnell gegen eine obere Dreiecksmatrix konvergiert. Startend mit der Ausgangsmatrix wird in seiner Grundidee im -ten Schritt die Matrix QR-zerlegt,

,

und anschließend werden die beiden Faktoren in umgekehrter Reihenfolge wieder zusammenmultipliziert:

,

um die neue Näherungsmatrix zu erhalten. Wegen ergibt sich und daraus ; es handelt sich bei dieser Umformung also tatsächlich um eine Ähnlichkeitstransformation mit einer orthogonalen Matrix. Wie eine genauere Analyse zeigt, besteht ein enger Zusammenhang zur Potenzmethode: Die QR-Iteration lässt sich auffassen als eine Potenzmethode, die simultan auf alle Vektoren einer Orthonormalbasis angewendet wird; durch die QR-Zerlegung in jedem Schritt wird dabei sichergestellt, dass diese Vektoren im Laufe der Iteration auch numerisch stabil orthonormiert bleiben (siehe auch Unterraumiteration). Aus dieser Darstellung ergibt sich auch ein Beweis, dass das Verfahren unter geringen Voraussetzungen an gegen eine obere Dreiecksmatrix konvergiert.

In dieser einfachen Form ist das QR-Verfahren aus zwei Gründen noch nicht für die Praxis geeignet. Zum einen ist der Rechenaufwand für die QR-Zerlegung, die in jedem Schritt bestimmt werden muss, sehr groß. Zum anderen findet die Konvergenz im Allgemeinen nur langsam statt, es müssen also viele Schritte durchgeführt werden, um eine gewünschte Genauigkeit zu erhalten. Dem ersten Punkt lässt dich dadurch begegnen, dass in einem Vorbereitungsschritt die Matrix durch Ähnlichkeitstransformationen auf Hessenberg-Gestalt gebracht wird. Das lässt sich durch Transformationen mit geeigneten Householder-Matrizen erreichen. Da eine Hessenberg-Matrix nur noch Nichtnulleinträge unter der Hauptdiagonale hat, lässt sie sich schnell mit den entsprechenden Givens-Rotationen QR-zerlegen. Wie sich leicht zeigen lässt, erhält ein Schritt des QR-Verfahrens Symmetrie und Hessenberg-Gestalt. Da eine symmetrische Hessenberg-Matrix eine Tridiagonalmatrix ist, vereinfacht sich das Verfahren im symmetrischen Fall nochmals erheblich. Die Konvergenzgeschwindigkeit kann ähnlich wie bei der inversen Vektoriteration deutlich erhöht werden, wenn in jedem Schritt anstelle der Matrix die Matrix mit einem geschickt gewählten Shiftparameter transformiert wird. Für die Wahl von , der Wert sollte eine Näherung an einen Eigenwert von sein, existieren verschiedene sogenannte Shiftstrategien.

Mit einer Variante des QR-Verfahrens kann auch die sogenannte Singulärwertzerlegung einer Matrix berechnet werden. Diese Verallgemeinerung der Diagonalisierung auf beliebige – sogar nicht quadratische – Matrizen wird in einigen Anwendungen, wie etwa in der Bildkompression, direkt verwendet. Mithilfe der Singulärwertzerlegung können auch große, schlecht konditionierte lineare Ausgleichsprobleme gelöst werden.

Krylow-Unterraum-Verfahren

Die Krylow-Unterraum-Verfahren mit ihren zahlreichen Varianten und Spezialisierungen sind die wichtigste Verfahrensgruppe zur Lösung sowohl von linearen Gleichungssystemen als auch von Eigenwertproblemen, wenn die gegebene Matrix sehr groß und dünnbesetzt ist. Der historisch erste Algorithmus aus dieser Gruppe ist das Verfahren der konjugierten Gradienten, kurz CG-Verfahren (von englisch conjugate gradients) zur Lösung linearer Gleichungssysteme mit symmetrischen und positiv definiten Koeffizientenmatrizen.

CG-Verfahren

Der fruchtbare Zusammenhang des CG-Verfahrens mit Krylow-Unterräumen wurde erst später erkannt, seine Grundidee ist eine andere: Es löst anstelle des Gleichungssystems ein dazu äquivalentes Optimierungsproblem. Ist nämlich symmetrisch und positiv definit, so ist die Lösung von die eindeutig bestimmte Minimalstelle der Funktion

Im zweidimensionalen Fall sind die Höhenlinien der zu minimierenden Funktion Ellipsen. Wählt man immer die Richtung des steilsten Abstieg, führt das zu einem Zickzackkurs (grün). Das CG-Verfahren verwendet konjugierte Richtungen und landet mit zwei Schritten genau im Minimum (rot).

.

Damit stehen grundsätzlich alle numerischen Verfahren zur Lösung von Optimierungsproblemen auch für das lineare Gleichungssystem zur Verfügung, insbesondere die sogenannten Abstiegsverfahren. Das sind iterative Verfahren, die ausgehend von der aktuellen Näherung im -ten Schritt entlang einer geeigneten Suchrichtung das eindimensionale Optimierungsproblem

„Suche , sodass minimal wird.“

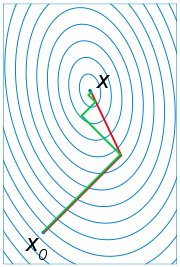
lösen. Die dabei gefundene Stelle wird die neue Näherung für den nächsten Schritt. Eine zunächst naheliegende Wahl für die Suchrichtung ist die Richtung des steilsten Abstiegs, was auf das Gradientenverfahren zur Bestimmung der Minimalstelle führt. Allerdings zeigt sich, dass die so berechneten Näherungen sich im Allgemeinen nur sehr langsam und in einem „Zickzackkurs“ der wahren Lösung annähern. Wesentlich besser geeignet sind Suchrichtungen, die die spezielle Gestalt der zu minimierenden Funktion berücksichtigen. Die Niveaumengen von sind -dimensionale Ellipsoide (im anschaulichen, zweidimensionalen Fall Ellipsen), daher ist es günstig, die Suchrichtungen zueinander konjugiert zu wählen (im Anschauungsfall entspricht das den konjugierten Durchmessern). Dabei heißen zwei Richtungen und konjugiert, wenn gilt. Das CG-Verfahren wählt daher für die erste Suchrichtung die Richtung des steilsten Abstiegs, aber die folgenden so, dass alle Suchrichtungen zueinander konjugiert sind. Es lässt sich zeigen, dass dann nach Abstiegen die wahre Lösung erreicht wird. Meist ist aber eine ausreichend genaue Näherungslösung schon nach deutlich weniger Schritten erreicht und das Verfahren kann vorzeitig abgebrochen werden.

Vom CG-Verfahren zu den Krylow-Unterraum-Verfahren

In den Rechenschritten des CG-Verfahrens geht die Matrix nur in der Form von Matrix-Vektor-Produkten ein. Sie selbst wird nicht zerlegt oder umgeformt – ein großer Vorteil, wenn sie dünnbesetzt ist. Nimmt man zur Vereinfachung (aber ohne Beschränkung der Allgemeinheit) an, dass als Startvektor der Nullvektor gewählt wird, so zeigt eine genauere Analyse, dass jede Näherung eine Linearkombination der Vektoren ist, also aus wiederholten Multiplikationen der rechten Seite mit aufgebaut wird. Anders ausgedrückt: Jedes liegt in einem Krylow-Unterraum

.

Diese Eigenschaft ist das Kennzeichen der Krylow-Unterraum-Verfahren: Sie erzeugen iterativ für Näherungen mit . Dabei wird zusätzlich so gewählt, dass das Residuum in einem noch festzulegenden Sinne möglichst klein ist. Beim CG-Verfahren ist die Bedingung nicht unbedingt naheliegend, aber für die spezielle Struktur des Problems gut geeignet: Mit der durch gewichteten Vektornorm ist in jedem Schritt minimal. Der Nachteil liegt dabei darin, dass dies nur funktioniert, wenn tatsächlich symmetrisch und positiv definit ist, anderenfalls ist gar keine Norm. Im Allgemeinen werden die Zusatzbedingungen, die Krylow-Unterraum-Verfahren an die Wahl von stellen, als sogenannte Projektionsbedingung formuliert. Man verlangt dabei, dass das Residuum orthogonal zu allen Vektoren aus einem -dimensionalen Unterraum ist, in Symbolen

.

Die sind normalerweise selbst Krylow-Unterräume, im einfachsten Fall, wie auch beim CG-Verfahren, zum Beispiel . Für die konkrete Berechnung der Näherungen werden sukzessive Orthonormalbasen der beteiligten Krylow-Unterräume aufgebaut. Das bekannte Gram-Schmidt-Verfahren zur Orthonormalisierung ist in seiner Standardform leider numerisch instabil. Es lässt sich jedoch mit einer kleinen Modifikation stabilisieren.

Weitere Krylow-Unterraum-Verfahren

Ein Vergleich der Norm des Fehlers sowie des Residuums beim CG-Verfahren (blau) und dem MINRES-Verfahren (grün). Das auf positiv definite Matrizen spezialisierte CG-Verfahren konvergiert schneller als das allgemeinere MINRES-Verfahren.

Aus den genannten Grundideen ergeben sich zahlreiche Variationen, Anpassungen und Verbesserungen innerhalb dieser Verfahrensklasse, von denen nur einige exemplarisch genannt werden sollen. Eine direkte Verallgemeinerung des CG-Verfahrens ist das BiCG-Verfahren. Es hebt die Einschränkung auf symmetrische Matrizen dadurch auf, dass es zusätzlich zu dem mit gebildeten Krylow-Unterräumen, auch die zur transponierten Matrix gehörigen verwendet. Eine Optimierung, die die zusätzlichen Multiplikationen mit vermeidet, ist das CGS-Verfahren. Beide Verfahrenstypen sind in vielen praktischen Fällen instabil, bilden aber die Grundlage für verschiedene Stabilisierungsversuche, etwa in der Gruppe der BiCGSTAB-Verfahren. 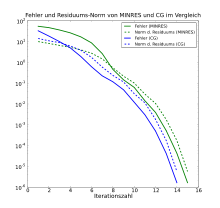Wichtige und im Allgemeinen stabile Verfahren sind GMRES und seine Spezialisierung für symmetrische Matrizen, MINRES. Sie setzen direkt bei den Residuen an und bestimmen im Krylow-Unterraum so, dass minimal ist. Weitere Verbesserungen dieses Grundprinzips sind etwa das QMR- und das TFQMR-Verfahren.

Krylow-Unterraum-Verfahren können nicht nur für sehr große dünnbesetzte lineare Gleichungssysteme verwendet werden, sondern auch zur Lösung ebensolcher Eigenwertprobleme – ein weiterer Grund für ihre große Bedeutung in der modernen numerischen linearen Algebra. Natürlich kann in Eigenwertproblemen nicht mit gestartet werden ( ist ja per Definition kein Eigenvektor). Es werden hier die Näherungen und zugehörige so bestimmt, dass

mit gilt. Dieses Vorgehen führt auf ein nur -dimensionales Eigenwertproblem, das sich für kleine leicht lösen lässt und Näherungen an einige Eigenwerte von liefert. Der zugehörige Grundalgorithmus ist das Arnoldi-Verfahren. Wie stets bei Eigenwertproblemen ergeben sich für symmetrische Matrizen deutliche Vereinfachungen; diese führen auf das Lanczos-Verfahren.

Literatur

• Steffen Börm, Christian Mehl: Numerical Methods for Eigenvalue Problems. Walter de Gruyter, Berlin/Boston 2012, ISBN 978-3-11-025033-6.
• Folkmar Bornemann: Numerische lineare Algebra – Eine konzise Einführung mit MATLAB und Julia. Springer Spektrum, Wiesbaden 2016, ISBN 978-3-658-12883-8.
• Biswa Nath Datta: Numerical Linear Algebra and Applications. 2. Auflage. SIAM, Philadelphia 2010, ISBN 978-0-89871-685-6.
• Andreas Meister: Numerik linearer Gleichungssysteme. 5. Auflage. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-07199-8.
• Jean-Luc Chabert u.a. (Hrsg.): A History of Algorithms. Springer, Berlin/Heidelberg 1999, ISBN 978-3-540-63369-3.
• Gene H. Golub, Henk A. van der Vorst: Eigenvalue computation in the 20th century. In: Journal of Computational and Applied Mathematics. Band 123, 2000, S. 35–65.

Basierend auf einem Artikel in: Wikipedia.de

Seite zurück
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.01. 2024