
Messabweichung
Messabweichung ist ein Begriff aus der Messtechnik bzw. Metrologie. Die Messabweichung ist definiert als eine Differenz zwischen Messwert und Referenzwert. (Die Bezeichnung Messfehler wird in der gegenwärtigen Norm nicht mehr verwendet, da nicht klar definiert ist, ob damit die Messabweichung, die Messunsicherheit oder gar ein grober Fehler gemeint ist, siehe Messfehler). Als Referenzwert kommt in Frage:
- Ein Wert mit vernachlässigbarer Unsicherheit oder ein vereinbarter Wert,
- der in DIN 1319-1 und DIN 55350-13 als richtiger Wert bezeichnet wird.
- ein mit der Definition einer Messgröße übereinstimmender wahrer Wert.
Messabweichungen haben grundsätzlich eine systematische und eine zufällige Komponente. Die systematische Komponente kann null werden, die zufällige nicht.
Vorbemerkung
Man sollte bei der Angabe eines Messwertes immer hinterfragen:
- Wie weit kann ich mich auf den angezeigten (ermittelten) Wert als korrekte Aussage über die zu messende Größe verlassen?
- Beispiel: Eine elektrische Stromstärke betrage exakt 5 A, wird auch exakt 5 A angezeigt?
- Wie weit kann ich mich auf den festgestellten Zahlenwert verlassen?
- Beispiel: Heißt die Angabe „5“: geschätzt zwischen 0 und 10, vielleicht auch 6, oder heißt die Angabe „5“ genau bis auf eine durch Schätzunsicherheit mögliche Abweichung ± 0,1? Im zweiten Falle wäre dann 5,0 zu schreiben. Das ist zwar mathematisch dasselbe, aber in der Messtechnik von anderer Qualität.
- Beispiel: Welchen Sinn hat die Angabe „4,8376“ bei einer durch Fehlergrenzen möglichen Abweichung ± 0,1? Die Angabe gaukelt eine nicht vorhandene Qualität vor und ist durch 4,8 zu ersetzen. Ohne Angabe über die Zuverlässigkeit einer Messaussage ist die Aussage von zweifelhaftem Wert.
Definitionen
Grundlage
In der Messtechnik wird unterschieden zwischen
= wahrer Wert der Messgröße als Ziel der Auswertungen von Messungen der Messgröße; das ist ein „ideeller Wert“, der in aller Regel nicht genau bekannt ist.
= richtiger Wert der Messgröße als „bekannter Wert“ für Vergleichszwecke, dessen Abweichung vom wahren Wert für den Vergleichszweck als vernachlässigbar betrachtet wird.
- Zwischen
und
besteht ein zwar prinzipieller, aber quantitativ unerheblicher Unterschied.
Gemäß Definition setzt sich ein
= angezeigter (ausgegebener) Wert
zusammen aus dem wahren Wert
und der Messabweichung
in der Form
.
Die Messabweichung ergibt sich daraus zu
.
Sie ist nicht genau bekannt, da der wahre Wert der Messgröße nicht genau bekannt ist.
Quantitative Angabe
Für quantitative Angaben unterscheidet man in der Praxis zwei Angaben:
Absolute Messabweichung
Zur Bestimmung einer Messabweichung wird der nicht bekannte wahre Wert durch
den bekannten richtigen Wert ersetzt,
und die Differenz zwischen beiden Werten wird zu diesem Zweck
vernachlässigt.
Die damit anstelle von
durch Rechnung festgestellte Abweichung
wird ebenfalls als Messabweichung oder vielfach als absolute Messabweichung
(auch absoluter Messfehler) bezeichnet
.
Diese Größe hat einen Betrag, ein Vorzeichen und eine Einheit, nämlich stets dieselbe wie die Messgröße.
Relative Messabweichung
In der Umrechnung
wird der Bruch als relative Messabweichung (auch relativer Messfehler)
bezeichnet
.
Diese Größe hat die Einheit Eins; sie kann positiv oder negativ sein.
- Anmerkung 1: Ein Wert
gibt keinen Anlass zu einer Messung. Zu diesem kann auch der relative Fehler nicht berechnet werden.
- Anmerkung 2: Es gilt:
für alle
. Ferner gilt: 100 % = 1.
Beispiel:
Verwechslungsgefahr: Im Zusammenhang mit Klassenzeichen wird überwiegend als Bezugsgröße (also im Nenner) statt des richtigen Wertes der Messbereichsendwert verwendet. Dann steht als bezogene Größe (also im Zähler) aber kein Fehler, sondern eine Fehlergrenze, was mit Definitionen zum Begriff Fehler bzw. Abweichung nichts zu tun hat.
Ursachen
- Messgeräteabweichungen als Folge der Unvollkommenheit der Konstruktion, Fertigung, Justierung (z.B. durch Werkstoffe, Fertigungstoleranzen)
- durch das Messverfahren bedingte Einflüsse infolge Einwirkung der Messeinrichtung auf die Messgröße (z.B. Rückwirkungsabweichung [Schaltungseinflussfehler] durch Eigenverbrauch des Messgerätes)
- Umwelteinflüsse als Folge von Änderungen der Einwirkungen aus der Umgebung (z.B. Temperatur, Refraktionsanomalien, äußere elektrische oder magnetische Felder, Einfluss der Raumlage, Erschütterungen)
- Instabilitäten des Wertes der Messgröße oder des Trägers der Messgröße (z.B. statistische Vorgänge, Rauschen)
- Beobachtereinflüsse infolge unterschiedlicher Eigenschaften und Fähigkeiten des Menschen (z.B. Aufmerksamkeit, Übung, Sehschärfe, Schätzvermögen, Parallaxe, Zeit- und Zielfehler)
Außerhalb der Diskussion hier stehen
- Verfälschungen durch Irrtümer des Beobachters (Grober Fehler),
- Verfälschungen durch Wahl ungeeigneter Mess- und Auswerteverfahren,
- Verfälschungen durch Nichtbeachtung bekannter Störgrößen.
Arten
Die Messabweichung eines unberichtigten Messergebnisses setzt sich additiv aus der systematischen Messabweichung und der zufälligen Messabweichung zusammen.
Systematische Messabweichung
Eine einseitig gerichtete Abweichung, die durch im Prinzip feststellbare Ursachen bedingt ist, ist eine systematische Abweichung.
- Bei Wiederholungen einer Messung unter gleichen Bedingungen liegt dieselbe systematische Messabweichung vor; sie ist aus den Messwerten nicht erkennbar.
- Eine systematische Messabweichung hat Betrag und Vorzeichen.
- Eine systematische Messabweichung setzt sich additiv aus einer bekannten und einer unbekannten systematischen Messabweichung zusammen.
- Zur Berechnung eines Messergebnisses wird der Messwert um die bekannte systematische Messabweichung berichtigt.
Zufällige Messabweichung
Eine nicht beherrschbare, nicht einseitig gerichtete Abweichung ist eine zufällige Abweichung.
- Bei Wiederholungen – selbst unter genau gleichen Bedingungen – werden die Messwerte voneinander abweichen; sie streuen.
- Zufällige Messabweichungen schwanken nach Betrag und Vorzeichen.
Es gilt zu unterscheiden:
- Durch systematische Messabweichungen wird ein Messergebnis immer unrichtig.
- Durch zufällige Messabweichungen wird ein Messergebnis immer unsicher.
Sonderfälle
Dynamische Messabweichung
Bei nicht stationären
Vorgängen entsteht eine dynamische Messabweichung. Der von einem Messgerät
gelieferte Wert
folgt der zeitlichen Änderung des Eingangssignals
im Allgemeinen verzögert.
Die Verzögerung kann häufig durch ein Tiefpassverhalten
beschrieben werden. Für den im eingeschwungenen (stationären) Zustand häufigen
Fall des proportionalen
Zusammenhangs
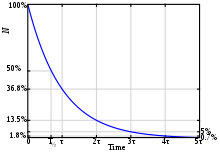
entsteht durch die Verzögerung eine dynamische Messabweichung (auch dynamischer Fehler)
.
Bei einer sprunghaften Änderung des Eingangssignals klingt diese Abweichung bei einem Verzögerungsglied wieder ab. Bei schwingungsfähigen Systemen ist dazu eine Dämpfung erforderlich.
Bei sinusförmigen Wechselgrößen mit variabler Frequenz entsteht ein Frequenzgang, durch den Amplitude und Phasenwinkel beeinflusst werden.
Quantisierungsmessabweichung
Bei einem Messgerät mit einem Analog-Digital-Umsetzer entsteht eine Messabweichung infolge der Digitalisierung.
Messgeräteabweichung
Jedes Messgerät enthält seit seiner Herstellung eine Messgeräteabweichung. Diese lässt sich durch Vergleich mit einem wesentlich besseren Messgerät bestimmen; sie ist also systematischer Natur und im Prinzip korrigierbar. Der Aufwand dazu ist allerdings hoch. Zum Umgang mit der Abweichung gibt es zwei Möglichkeiten, von denen eine vom Hersteller des Messgerätes geliefert werden sollte:
- Die Fehlerkurve eines Messgerätes ist die grafische Darstellung der Abweichung, aufgetragen in Abhängigkeit von der Anzeige; teilweise wird statt der Kurve auch eine Tabelle angegeben. Anhand der Fehlerkurve sind Betrag und Vorzeichen der Abweichung zu einem Messwert abzulesen; es ist möglich, Korrekturen vorzunehmen.
- Da die Fehlerkurve die Abweichung nur zu einem bestimmten Zeitpunkt und unter anzugebenden Einflussbedingungen dokumentiert, wird meistens darauf verzichtet, und der Hersteller garantiert lediglich Fehlergrenzen unter gewissen Bedingungen. Teilweise werden Fehlergrenzen pauschal durch Klassenzeichen beschrieben.
Fehlergrenze
Die Fehlergrenze ist
begrifflich streng vom Fehler zu unterscheiden. Sie sagt aus, wie groß der
Fehler dem Betrage nach höchstens werden darf. Dabei gibt es eine obere
und eine untere Fehlergrenze, vorzugsweise gleich groß, beschrieben durch die
vorzeichenlose Größe .
Der wahre Wert liegt (bei Abwesenheit einer zufälligen Abweichung) in einem
Bereich
.
Gelegentlich ist es möglich, ein Messverfahren zu verbessern und so die Fehlergrenzen zu verkleinern; dabei bleibt es die Frage, ob sich der erhöhte (Kosten-)Aufwand lohnt.
In vielen Bereichen sind die Fehlergrenzen Gegenstand von Vorschriften; dann sind Eichämter und industrielle Fachlabore damit zu befassen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 10.05. 2024